Category Archives: Derivatives

Adapting 2021 AB 5

Posted on by
3

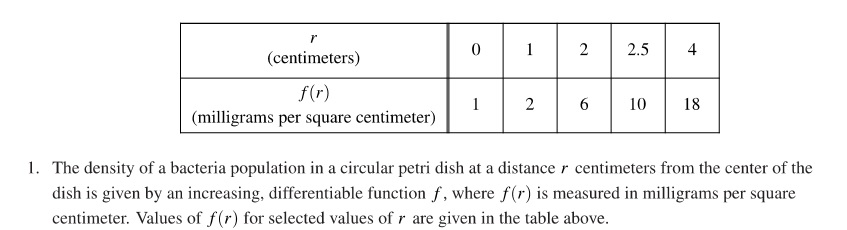
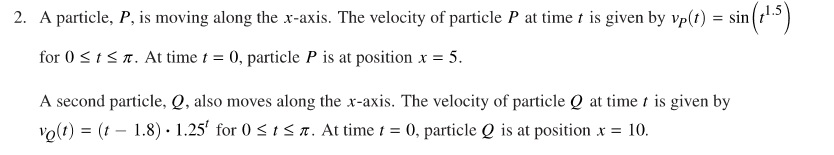Five of nine. Continuing the current series of posts, this post looks at the AB Calculus 2021 exam question AB 5. The series considers each question with the aim of showing ways to use the question in with your class as is, or by adapting and expanding it.  Like most of the AP Exam questions there is a lot more you can ask from the stem and a lot of other calculus you can discuss.

2021 AB 5

This question tests the process of differentiating an implicit function. In my scheme of type posts, it is in the Other Problems (Type 7) category; this type includes the topics of implicit functions, related rate problems, families of functions and a few others. This topic is in Unit 3 of the current Course and Exam Description. Every few exams one of these appears on the exams, but not often enough to be made into its own type.

The question does not lend itself to changes that emphasize the same concepts. Some of the suggestions below are for exploration beyond what is likely to be tested on the AP Exams.

Here is the stem, only one line long:

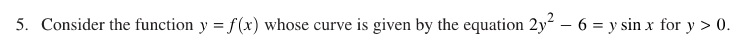
Part (a): Students were given dy/dx and asked to verify that the expression is correct. This is done so that a student who makes a mistake (or cannot find the derivative at all) will not be shut out of the rest of the question by not having the correct first derivative.

While not required for the exam, you could use a grapher in implicit mode to graph the relation. Without the y > 0 restriction the graph consists of two seemingly parallel graphs similar to a sine graph. They are not sine graphs.

Ideas for exploring this question:

  • Using a graphing utility that allows you to use sliders. Replace the -6 by a variable that will allow you to see all the members of this family using a slider.
  • If the slider value is between -1/8 and 0 the graph no longer looks the same. Explore with this.
  • If the slider value is < -1/8 there is no graph. Why?
  • Explain why these are not sine graphs. (Hint: Use the quadratic formula to solve for y):

\displaystyle y=\frac{{\sin (x)\pm \sqrt{{{{{(\sin (x))}}^{2}}+48}}}}{4}.

 Part (a): There is not much you can change in this part. Ask for the derivative of a different implicit relation. You may use other questions of this type. Good Question 17, 2004 AB 4, 2016 BC 4 (parts a, b, and c are suitable for AB).

Discussion and ideas for adapting this question:

  • Ask for the first derivative without showing student the answer.
  • Find the derivative from the expression when first solved for y. Show that this is equal to the given derivative.

Part (b): An easy, but important question: write the equation of the tangent line at a given point. Writing the equation of a line shows up somewhere on the exam every year. As always, use the point-slope form.

Discussion and ideas for adapting this question:

  • Use a different point.

Part (c): Students were asked to find the point in a specific interval where the tangent line is horizontal.

Discussion and ideas for adapting this question:

  • By enlarging the domain find other points where the tangent line is horizontal. (Not likely to be asked on the exam, but good exercise.)
  • Using y < 0 find where the tangent line is horizontal. (Not likely to be asked on the exam, but good exercise.)
  • Determine if the two parts of the graph are “parallel.”
  • Determine if the two parts of the graph are congruent to y=\tfrac{1}{4}\sin \left( x \right).

Part (d): Students were asked to determine if the point found in the previous part was a relative maximum, minimum or neither, and to justify their answer.  

Discussion and ideas for adapting this question:

  • Have students justify using the Candidates’ test (closed interval test).
  • Have students justify using the first derivative test.
  • Have students justify using the second derivative test.
  • Ask the same question for the branch with y < 0.

Having students justify local extreme values by all three methods is good practice any time there is a justification required. Depending on the problem, it may not be possible to use all three. Discuss why; discuss how to decide which is the most efficient for each problem.

Next week 2021 AB 6.

I would be happy to hear your ideas for other ways to use this question. Please use the reply box below to share your ideas.

Adapting 2021 AB 4 / BC 4

Posted on by
Reply

Four of nine. Continuing the series started in the last three posts, this post looks at the AP Calculus 2021 exam question AB 4 / BC 4. The series considers each question with the aim of showing ways to use the question with your class as is, or by adapting and expanding it.  Like most of the AP Exam questions there is a lot more you can ask from the stem and a lot of other calculus you can discuss.

2021 AB 4 / BC 4

This is a Graph Analysis Problem (type 3) and contains topics from Units 2, 4, and 6 of the current Course and Exam Description. The things that are asked in these questions should be easy for the students, however each year the scores are low. This may be because some textbooks simply do not give students problems like this. Therefore, supplementing with graph analysis questions from past exams is necessary.

There are many additional questions that can be asked based on this stem and the stems of similar problems. Usually, the graph of the derivative is given, and students are asked questions about the graph of the function. See Reading the Derivative’s Graph.

Some years this question is given a context, such as the graph is the velocity of a moving particle. Occasionally there is no graph and an expression for the derivative or function is given.

Here is the 2021 AB 4 / BC 4 stem:

The first thing students should do when they see G\left( x \right)=\int_{0}^{x}{{f\left( t \right)}}dt is to write prominently on their answer page {G}'\left( x \right)=f\left( x \right) and \displaystyle {G}''\left( x \right)={f}'\left( t \right). While they may understand and use this, they must say it.

Part (a): Students were asked for the open intervals where the graph is concave up and to give a reason for their answer. (Asking for an open interval is to remove any concern about the endpoints being included or excluded, a place where textbooks differ. See Going Up.)

Discussion and ideas for adapting this question:

  • Using this or similar graphs go through each of these with your class until the answers and reasons become automatic. There are quite a few other things that may be asked here based on the derivative.
    • Where is the function increasing?
    • Decreasing?
    • Concave down, concave up?
    • Where are the local extreme values?
    • What are the local extreme values?
    • Where are the absolute extreme values?
    • What are the absolute extreme values?
  • There are also integration questions that may be asked, such as finding the value of the functions at various points, such as G(1) = 2 found by using the areas of the regions. Also, questions about the local extreme values and the absolute extreme value including their values. These questions are answered by finding the areas of the regions enclosed by the derivative’s graph and the x-axis. Parts (b) and (c) do some of this.
  • Choose different graphs, including one that has the derivative’s extreme value on the x­-axis. Ask what happens there.

Part (b): A new function is defined as the product of G(x) and f(x) and its derivative is to be found at a certain value of x. To use the product rule students must calculate the value of G(x) by using the area between f(x) and the x-­axis and the value of {f}'\left( x \right) by reading the slope of f(x) from the graph.

Discussion and ideas for adapting this question:

  • This is really practice using the product rule. Adapt the problem by making up functions using the quotient rule, the chain rule etc. Any combination of \displaystyle G,{G}',{G}'',f,{f}',\text{ or }{f}'' may be used. Before assigning your own problem, check that all the values can be found from the given graph.
  • Different values of x may be used.

Part (c): Students are asked to find a limit. The approach is to use L’Hospital’s Rule.

Discussion and ideas for adapting this question:

  • To use L’Hospital’s Rule, students must first show clearly on their paper that the limit of the numerator and denominator are both zero or +/- infinity. Saying the limit is equal to 0/0 is considered bad mathematics and will not earn this point. Each limit should be shown separately on the paper, before applying L’Hospital’s Rule.
  • Variations include a limit where L’Hospital’s Rule does not apply. The limit is found by substituting the values from the graph.
  • Another variation is to use a different expression where L’Hospital’s Rule applies, but still needs values read from the graph.

Part (d): The question asked to find the average rate of change (slope between the endpoints) on an interval and then determine if the Mean Value Theorem guarantees a place where \displaystyle {G}' equals this value. Students also must justify their answer.

Discussion and ideas for adapting this question:

  • To justify their answer students must check that the hypotheses of the MVT are met and say so in their answer.
  • Adapt by using a different interval where the MVT applies.
  • Adapt by using an interval where the MVT does not apply and (1) the conclusion is still true, or (b) where the conclusion is false.

Next week 2021 AB 5.

I would be happy to hear your ideas for other ways to use this questions. Please use the reply box below to share your ideas.

Adapting 2021 AB 3 / BC 3

Posted on by
Reply

Three of nine. Continuing the series started in the last two posts, this post looks at the AB Calculus 2021 exam question AB 3 / BC 3. The series considers each question with the aim of showing ways to use the question in with your class as is, or by adapting and expanding it. Like most of the AP Exam questions there is a lot more you can ask from the stem and a lot of other calculus you can discuss.

2021 AB 3 / BC 3

This question is an Area and Volume question (Type 4) and includes topics from Unit 8 of the current Course and Exam Description. Typically, students are given a region bounded by a curve and an line and asked to find its area and its volume when revolved around a line. But there is an added concept here that we will look at first.

The stem is:

First, let’s consider the c. This is a family of functions question. Family of function questions appear now and then. They are discussed in the post on Other Problems (Type 7) and topics from Unit 8 of the current Course and Exam Description. My favorite example is 1998 AB 2, BC 2. Also see Good Question 2 and its continuation.

If we consider the function with c = 1 to be the parent function \displaystyle P\left( x \right)=x\sqrt{{4-{{x}^{2}}}} then the other members of the family are all of the form \displaystyle c\cdot P\left( x \right). The c has the same effect as the amplitude of a sine or cosine function:

  • The x-axis intercepts are unchanged.
  • If |c| > 1, the graph is stretched away from the x-axis.
  • If 0 < |c| < 1, the graph is compressed towards the x-axis.
  • And if c < 0, the graph is reflected over the x-axis.

All of this should be familiar to the students from their work in trigonometry. This is a good place to review those ideas. Some suggestions on how to expand on this will be given below.

Part (a): Students were asked to find the area of the region enclosed by the graph and the x-axis for a particular value of c. Substitute that value and you have a straightforward area problem.

Discussion and ideas for adapting this question:

  • The integration requires a simple u-substitution: good practice.
  • You can change the value of c > 0 and find the resulting area.
  • You can change the value of c < 0 and find the resulting area. This uses the upper-curve-minus-the-lower-curve idea with the upper curve being the x-axis (y = 0).
  • Ask students to find a general expression for the area in terms of c and the area of P(x).
  • Another thing you can do is ask the students to find the vertical line that cuts the region in half. (Sometimes asked on exam questions).
  • Also, you could ask for the equation of the horizontal line that cuts the region in half. This is the average value of the function on the interval. See these post 1, 2, 3, and this activity 4.

Part (b): This question gave the derivative of y(x) and the radius of the largest cross-sectional circular slice. Students were asked for the corresponding value of c. This is really an extreme value problem. Setting the derivative equal to zero and solving the equation gives the x-value for the location of the maximum. Substituting this value into y(x) and putting this equal to the given maximum value, and you can solve for the value of c.  

(Calculating the derivative is not being tested here. The derivative is given so that a student who does not calculate the derivative correctly, can earn the points for this part. An incorrect derivative could make the rest much more difficult.)

Discussion and ideas for adapting this question:

  • This is a good problem for helping students plan their work, before they do it.
  • Changing the maximum value is another adaption. This may require calculator work; the numbers in the question were chosen carefully so that the computation could be done by hand. Nevertheless, doing so makes for good calculator practice.

Part (c): Students were asked for the value of c that produces a volume of 2π. This may be done by setting up the volume by disks integral in terms of c, integrating, setting the result equal to 2π, and solving for c.

Discussion and ideas for adapting this question:

  • Another place to practice planning the work.
  • The integration requires integrating a polynomial function. Not difficult, but along with the u-substitution in part (a), you have an example to show people that students still must do algebra and find antiderivatives.
  • Ask students to find a general expression for the volume in terms of c and the volume of P(x).
  • Changing the given volume does not make the problem more difficult.

Next week 2021 AB 3/ BC 3.

I would be happy to hear your ideas for other ways to use this questions. Please use the reply box below to share your ideas.

Adapting 2021 AB 2

Posted on by
Reply

Two of nine. Continuing the series started in my last post, this post looks at the AB Calculus 2021 exam question AB 2. The series looks at each question with the aim of showing ways to use the question in with your class as is or by adapting and expanding it.  Like most of the AP Exam questions there is a lot more you can ask from the stem and a lot of other calculus you can discuss.

2021 AB 2

This is a Linear Motion Problem (Type 2) and has topics from Unit 4 of the current Course and Exam Description. Two particles are moving on the x-axis and the questions ask about their motion individually and relative to each other. The velocity and initial position are given for each particle. Parts (a), (c), and (d) are typical; (b) is the core of the problem.

The stem is:

Part (a): Students are asked to find the position of each particle at time t = 1.

Discussion and ideas for adapting this question:

  • The expected approach is to calculate for each particle the initial position plus the displacement from t = 0 to t = 1. So, for P the computation is  P\left( 1 \right)=5+\int_{0}^{1}{{\sin \left( {{{t}^{{1.5}}}} \right)}}dt and similarly for Q(1). This is a calculator allowed question and students should use their calculator to find the answer and not do it by hand.
  • A different approach is to work it as an initial value differential equation problem. This will work but takes longer than the approach suggested above.
  • In class, it is worth discussing both methods.
  • You can adapt this by using a different time.
  • Another question is to find (only) the displacement if each particle over some time interval. Displacement has been asked in other years.
  • Ask “Will the particles ever collide? If so when and justify your answer. (Answer: no)

Part (b): Students were asked to determine if the particles are moving apart or towards each other at time t = 1. This is the main question and requires a careful analysis of their motion.

Discussion and ideas for adapting this question:

  • To determine this, students need to consider the velocity of the particles and their position (from part (a)). P is to the left of Q and moving right. Q is to the right of P and moving left, therefore, the distance between them is decreasing.
  • You can practice this analysis by using different times.
  • Ask students to carefully describe the motion of one or both particles: when it is moving left and right, when it changes direction, find the local maximum and minimum positions, etc. Notice that this is really the same as analyzing the shape of a graph. The connection between the two problems will help students understand both better. See: Motion Problems: Same Thing, Different Context

Part (c): A question about speed.

Discussion and ideas for adapting this question:

  • A typical question. Students should compare the signs of the velocity and acceleration of the particle. If they are the same, the speed is increasing; if different, decreasing.
  • You may ask this of the other particle.
  • You may ask this at different times.
  • See previous posts on speed here and here.

Part (d): Students were required to find the total distanced traveled by Q on the interval [0, π].

Discussion and ideas for adapting this question:

  • Since speed is the absolute value of the velocity, integrate the absolute value of the velocity. Do this on a calculator.
  • Adapt this by using a different interval.
  • Adapt this by using the other particle.
  • Another (longer) way to approach this question is to find where the particle changes direction by finding where the velocity changes from negative to positive and/or vice versa (i.e., the local extreme values). Then find the distanced traveled on each part of the “trip,” and add or subtract. This will reinforce a lot of the concepts involved in linear motion; that is why it is worth doing. As for the exam, integrating the absolute value is the way to go. However, if this were a non-calculator question, then it would have to be done this way. Find a simpler velocity and try it both ways.
  • To integrate the absolute value by hand, it is necessary to break the interval into subintervals depending on where the velocity is positive or negative. This is the same as the approach in the bullet immediately above. This, too, is worth showing to reinforce the definition of absolute value.

2021 revised as an in-out question.

There was some unhappiness over the fact that the 2021 AB Calculus exam did not have an in-out questions (Rate and Accumulation Type 1). However, this question does have two rates going in opposite directions. So, just to be ornery, I rewrote it as an in-out questions by changing the context and units while keeping the same velocity functions. The point is that the situation tested can be reframed in other ways. Seeing the same thing in different dress may help students concentrate on the calculus involved. Here it is:

A factory processes cement at the rate of  \displaystyle {{v}_{p}}\left( t \right)=\sin \left( {{{t}^{{1.5}}}} \right) tons per hour for \displaystyle 0\le t\le \pi hours. At time t = 0 the amount on hand is P = 5 tons.

The factory ships the cement at a rate given by  \displaystyle {{v}_{Q}}\left( t \right)=\left( {t-1.8} \right){{1.25}^{t}} tons per hour for \displaystyle 0\le t\le \pi hours. At time t = 0 the amount shipped is 10 tons.

  1. Find the amount processed and the amount shipped after hour.
  2. Is the amount on hand increasing or decreasing at time t = 1? Explain your reasoning.
  3. At what rate is the rate at which the cement is being shipped changing at t = 1? Is the amount being shipped increasing or decreasing at t = 1? Explain your reasoning.
  4. Find the total amount of cement processed over the time interval \displaystyle 0\le t\le \pi .

Next week 2021 AB 3/ BC 3.

I would be happy to hear your ideas for other ways to use this questions. Please use the reply box below to share your ideas.

Adapting 2021 AB 1 / BC 1

Posted on by
1

First of nine. One of the things many successful AP Calculus teachers do is to use past AP exam questions throughout the year. Individual multiple-choice exam questions are used as the topics they test are taught; free-response questions are adapted and expanded. There are several ways to do this:

  • Assign parts of a free-response (FR) question as is as the topic it tests is taught. Later, other parts from the same stem can be assigned. Including previously assigned parts is a spiraling technique. Once students see that you are doing this, they will be more likely to keep up to date on past topics.
  • Adapting and expanding the questions is another way to use FR questions.

This summer I will be discussing how to do just that. Each week I will look at one of the released 2021 FR questions and suggest how to expand and adapt it. Each stem allows for many more questions than can be asked on any one exam. You have the luxury of asking other things based on the same stem.

This summer’s series of posts will take one question at a time discuss it and suggest additional questions or explorations that may be asked. I will not be presenting solutions. They are available on AP Community bulletin board here and here. I will link the posts to the scoring standards when they are published.

2021 AB 1 / BC 1

This is a Reimann sum and Table question (Type 5) and covers topics from Units 6 and 8 from the current Course and Exam Description. All four parts are fairly typical for this type of problem. There is a little twist in part (b). The context is the density of bacteria growing in a petri dish.

Density is not listed in the Course and Exam Description. It is not covered well in many textbooks. Since it is not listed you need not teach it; exam questions referencing density have enough included information so that a student who has never seen the concept will still be able to answer the question. Keep this in mind as you look at each part; help your students see past the context and look at the calculus. More information on density see these posts Density Functions, and Good Question 15 and Good Question 16.

The stem for 2021 AB 1 / BC 1 reads:

Part (a): Students were asked to estimate the value of the derivative of f at r = 2.25 and explain its meaning, including units, in the context of the problem.  The expected procedure is to find the slope between the two values closest to r =2.25. The interpretation is the increase in density as you move away from the center. The units are milligrams per square centimeter per centimeter distant from the center \frac{{mg/c{{m}^{2}}}}{{cm}}.

Discussion and ideas for adapting this question:

  • AP exams have always asked this question at a value exactly half-way between two values in the table. You may change this to some other place such as r = 3 or r = 0.8.
  • Units of the derivative are always the units of the function divided by the units of the independent variable. Be sure your students understand this.
  • The units can be correctly written as  \frac{{mg}}{{c{{m}^{3}}}}, but here is a good change to discuss what the units mean. Why does “milligrams per square centimeter per centimeter distant from the center” make more sense?
  • Ask “Is there a point in the interval [2, 2.5] where the slope of the tangent line is 8? Justify your answer.” This makes use of the Mean Value Theorem.

Part (b) : As usual in this type of problem, students are asked to write a Riemann sum based on the intervals in the table. The difference here is that the integral being approximated, \displaystyle 2\pi \int_{0}^{4}{{rf\left( r \right)}}dr, has an “extra” factor of r in it.

Discussion and ideas for adapting this question:

  • The question asked for a right Riemann sum. You can easily adapt this by asking for a left Riemann sum, a midpoint Riemann sum, and/or a Trapezoidal approximation.
  • You may ask for a Riemann sum without the “extra” factor.
  • You may find a different Riemann sum problem and include an “extra” factor in it.
  • The integral is the integral for a radial density function. See the Density blog post cited above, example 2.
  • The radial density function looks like the integral for finding volumes by the method of cylindrical shells. This is more than a coincidence. Why?

Part (c): This part asked if the answer in (b) is an overestimate or an underestimate, with an explanation. For any approximation, some idea of its accuracy is important. In BC questions on power series approximations, a numerical estimate of the error bound is a common question.

Discussion and ideas for adapting this question:

  • Ask the same question for a different Riemann sum (left, midpoint, trapezoid).
  • The error in right and left Riemann sums estimates depend on whether the function is increasing or decreasing, and therefore on the first derivative. Midpoint and Trapezoidal approximation estimates are related to the concavity and therefore to the second derivative. See: Good Question 4)
  • A visual idea helps keep all this straight. Draw sketches showing the Riemann sum rectangles or trapezoids. Whether they lie above or below the graph of the function determines whether the approximation is an overestimate or underestimate.

Part (d): Typical of the Riemann sum table question is the final part with a related question based on a function and not based on the table.

Discussion and ideas for adapting this question:

  • This is a calculator allowed question. Students should not try to do the integration by hand.
  • The question asked for the average value of the function on an interval. Other questions you could ask are find the rate of change (derivative) at a point, the total mass \int_{1}^{4}{{rf\left( r \right)}}dr (note “extra” r), the average rate of change on an interval, etc.

Next week 2021 AB 2.

I would be happy to hear your ideas for other ways to use these questions. Please use the reply box below to share your ideas.

Other Asymptotes

Posted on by
6

A few days ago, a reader asked if you could find the location of horizontal asymptotes from the derivative of a function. The answer, alas, is no. You can determine that a function has a horizontal asymptote from its derivative, but not where it is. This is because a function and its many possible vertical translations have the same derivative but different horizontal asymptotes. To locate it precisely, we need more information, an initial condition (a point on the curve).

I have written a post about the relationship between vertical asymptotes and the derivative of the function here. Today’s post will discuss horizontal asymptotes and their derivatives.

Definition: a straight line associated with a curve such that as a point moves along an infinite branch of the curve the distance from the point to the line approaches zero and the slope of the curve at the point approaches the slope of the line. (Merriam-Webster dictionary). Thus, asymptotes can be vertical, horizontal, or slanted.

Horizontal Asymptotes

Horizontal asymptotes are a form of end behavior: they appear as \displaystyle x\to \infty or \displaystyle x\to -\infty . Specifically, if a function has a horizontal asymptote(s), then \displaystyle \underset{{x\to \pm \infty }}{\mathop{{\lim }}}\,{f}'\left( x \right)=0,  At an asymptote, the curve must approach a horizontal line, therefore its slope must be approaching zero as \displaystyle x\to \infty or \displaystyle x\to -\infty .  The converse is not true: If the derivative approaches zero, the function may not have a horizontal asymptote. A counterexample is \displaystyle f\left( x \right)=\sqrt[3]{x}.

In the first four examples that follow, the derivative approaches 0 as \displaystyle x\to \infty and/or \displaystyle x\to -\infty . 

Example 1: \displaystyle {f}'\left( x \right)=\frac{1}{{1+{{x}^{2}}}}  (Figure 1 in blue).This is the derivative of \displaystyle f\left( x \right)={{\tan }^{{-1}}}(x),\ -\tfrac{\pi }{2}<f\left( x \right)<\tfrac{\pi }{2}. (Figure 1 in red). We see that the derivative approaches zero in both directions, this tells us that there may be horizontal asymptote(s). We must look at the function to find where they are: \displaystyle y=\tfrac{\pi }{2} and \displaystyle y=-\tfrac{\pi }{2}

Polar Equations for AP Calculus

Posted on by
Reply

A recent thread on the AP Calculus Community bulletin boards concerned polar equations. One teacher observed that her students do not have a very solid understanding of polar graphs when they get to calculus. I expect this is a common problem. While ideally the polar coordinate system should be a major topic in pre-calculus courses, this is sometimes not the case. Some classes may even omit the topic entirely. Getting accustomed to a new coordinate scheme and a different way of graphing is a challenge.  I remember not having that good an understanding myself when I entered college (where first-year calculus was a sophomore course). Seeing an animated version much later helped a lot. 

This blog post will discuss the basics of polar equations and their graphs. It will not be as much as students should understand, but I hope the basics discussed here will be a help. There are also some suggestions for extending the study of polar function as the end.

Instead of using the Cartesian approach of giving every point in the plane a “name” by giving its distance from the y-axis and the x-axis as an ordered pair (x,y), polar coordinates name the point differently. Polar coordinates use the ordered pair (r, θ), where r, gives the distance of the point from the pole (the origin) as a function of θ, the angle that the ray from the pole (origin) to the point makes with the polar axis, (the positive half of the x-axis).

Start with this Desmos graph. It will help if you open it and follow along with the discussion below. The equation in the example is \displaystyle r(\theta )=2+4\sin (\theta ) You may change this to explore other graphs. (Because of the way Desmos graphs, you cannot have a slider for θ; the a-slider will move the line and the point on the graph. r(a) gives the value of r(θ).

  • Notice that as the angle changes the point at varying distance from the pole traces a curve. 
  • Move the slider to π/6. Since sin(π/6) = 0.5, r(π/6) = 4. The red dot is at the point (4, π/6). Move the slider to other points to see how they work. For example, θ = π/2 gives the point (6,π/2).
  • When the slider gets to θ = 7π/6, r = 0 and the point is at the pole. After this the values of r are negative, and the point is now on the ray opposite to the ray pointing into the third and fourth quadrants. The dashed line turns red to remind you of this.
  • As we continue around, the point returns to the origin at θ = 11π/6, then values are again positive. 
  • The graph returns to its starting point when θ = 2π. Note (2,0) is the same point as (2, 2π).
  • Even though this is the graph of a function, some points may be graphed more than once and the vertical line test does not apply. 
  • If we continued around, the graph will retrace the same path. This often happens when the polar function contains trig functions with integer multiples of θ.
    • This does not usually happen if no trig functions are involved – try the spiral r = θ.
    • If you enter non-integer multiples of θ and extend the domain to large values, vastly different graphs will appear, often making nice designs. Try \displaystyle r\left( \theta \right)=2+4\sin \left( {1.3\theta } \right) for \displaystyle 0\le \theta \le 20\pi . This is an area for exploration (if you have time).

In pre-calculus courses several families of polar graphs are often studied and named. For example, there are cardioids, rose curves, spirals, limaçons, etc. The AP Exams do not refer to these names and students are not required to know the names. The exception is circles which have the following forms where R is the radius: θ=R, r = Rsin(θ) or r = Rsin(θ)

To change from polar to rectangular for use the equations x=r\cos \left( \theta  \right) and  y=r\sin \left( \theta  \right). This is simple right triangle trigonometry (draw a perpendicular from the point to the x-axis and from there to the pole). 

To change from rectangular to polar form use  r=\sqrt{{{{x}^{2}}+{{y}^{2}}}} and  \displaystyle \theta =\arctan \left( {\tfrac{y}{x}} \right)

AP Calculus Applications

There are two applications that are listed on the AP Calculus Course and Exam Description: using and interpreting the derivative of polar curves (Unit 9.7) and finding the area enclosed by a polar curve(s) (Units 9.8 and 9.9).

Since calculus is concerned with motion, AP Students should be able to analyze polar curves for how things are changing:

  • The rate of change of r away from or towards the pole is given by  \displaystyle \frac{{dr}}{{d\theta }}
  • The rate of change of the point with respect to the x-direction is given by  \displaystyle \frac{{dx}}{{d\theta }} where \displaystyle x=r\cos \left( \theta \right) from above.
  • The rate of change of the point with respect to the y-direction is given by  \displaystyle \frac{{dy}}{{d\theta }} where \displaystyle y=r\sin \left( \theta \right)from above.
  • The slope of the tangent line at a point on the curve is \displaystyle \frac{{dy}}{{dx}}=\frac{{dy/d\theta }}{{dx/d\theta }}. See 2018 BC5 (b)

Area

 \displaystyle \underset{{\Delta \theta \to 0}}{\mathop{{\lim }}}\,\sum\limits_{{i=1}}^{\infty }{{\tfrac{1}{2}}}{{r}_{i}}^{2}\Delta \theta =\tfrac{1}{2}\int_{{{{\theta }_{1}}}}^{{{{\theta }_{2}}}}{{{{r}^{2}}d\theta }}

CAUTION: In using this formula, we need to be careful that the curve does not overlap itself. In the Desmos example, the smaller loop overlaps the larger loop; integrating from 0 to 2π counts the inner loop twice. Notice how this is handled by considering the limits of integration dividing the region into non-overlapping regions: 

  • The area of the outer loop is  \displaystyle \tfrac{1}{2}\int_{{-\pi /6}}^{{7\pi /6}}{{{{{(2+4\sin (\theta ))}}^{2}}d\theta }}\approx 35.525
  • The area of the inner loop is  \displaystyle \tfrac{1}{2}\int_{{7\pi /6}}^{{11\pi /6}}{{{{{(2+4\sin (\theta ))}}^{2}}d\theta }}\approx 2.174
  • Integrating over the entire domain gives the sum of these two:  \displaystyle \tfrac{1}{2}\int_{0}^{{2\pi }}{{{{{(2+4\sin (\theta ))}}^{2}}d\theta }}=12\pi \approx 37.699. This is not the correct area of either part. 

This problem can be avoided by considering the geometry before setting up the integral: make sure the areas do not overlap. Restricting r to only non-negative values is often required by the fine print of the theorem in textbooks, but this restriction is not necessary when finding areas and makes it difficult to find, say, the area of the smaller inner loop of the example. Here is another example: 

\displaystyle r\left( \theta \right)=\cos \left( {3\theta } \right). Between 0 and \displaystyle 2\pi this curve traces the same path twice.