Adapting 2021 AB 2

Posted on June 29, 2021 by Lin McMullin

Two of nine. Continuing the series started in my last post, this post looks at the AB Calculus 2021 exam question AB 2. The series looks at each question with the aim of showing ways to use the question in with your class as is or by adapting and expanding it. Like most of the AP Exam questions there is a lot more you can ask from the stem and a lot of other calculus you can discuss.

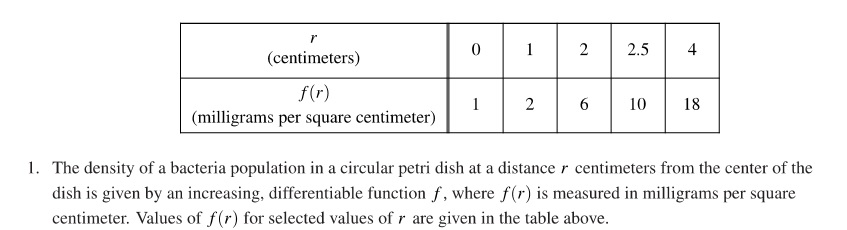
2021 AB 2

This is a Linear Motion Problem (Type 2) and has topics from Unit 4 of the current Course and Exam Description. Two particles are moving on the x-axis and the questions ask about their motion individually and relative to each other. The velocity and initial position are given for each particle. Parts (a), (c), and (d) are typical; (b) is the core of the problem.

The stem is:

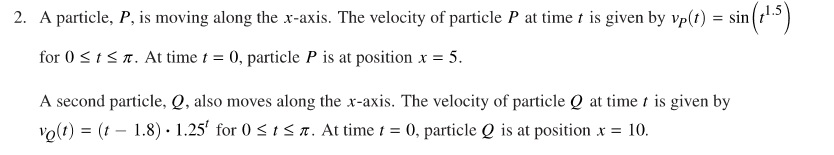
Part (a): Students are asked to find the position of each particle at time t = 1.

Discussion and ideas for adapting this question:

The expected approach is to calculate for each particle the initial position plus the displacement from t = 0 to t = 1. So, for P the computation is $P\left( 1 \right)=5+\int_{0}^{1}{{\sin \left( {{{t}^{{1.5}}}} \right)}}dt$ and similarly for Q(1). This is a calculator allowed question and students should use their calculator to find the answer and not do it by hand.
A different approach is to work it as an initial value differential equation problem. This will work but takes longer than the approach suggested above.
In class, it is worth discussing both methods.
You can adapt this by using a different time.
Another question is to find (only) the displacement if each particle over some time interval. Displacement has been asked in other years.
Ask “Will the particles ever collide? If so when and justify your answer. (Answer: no)

Part (b): Students were asked to determine if the particles are moving apart or towards each other at time t = 1. This is the main question and requires a careful analysis of their motion.

Discussion and ideas for adapting this question:

To determine this, students need to consider the velocity of the particles and their position (from part (a)). P is to the left of Q and moving right. Q is to the right of P and moving left, therefore, the distance between them is decreasing.
You can practice this analysis by using different times.
Ask students to carefully describe the motion of one or both particles: when it is moving left and right, when it changes direction, find the local maximum and minimum positions, etc. Notice that this is really the same as analyzing the shape of a graph. The connection between the two problems will help students understand both better. See: Motion Problems: Same Thing, Different Context

Part (c): A question about speed.

Discussion and ideas for adapting this question:

A typical question. Students should compare the signs of the velocity and acceleration of the particle. If they are the same, the speed is increasing; if different, decreasing.
You may ask this of the other particle.
You may ask this at different times.
See previous posts on speed here and here.

Part (d): Students were required to find the total distanced traveled by Q on the interval [0, π].

Discussion and ideas for adapting this question:

Since speed is the absolute value of the velocity, integrate the absolute value of the velocity. Do this on a calculator.
Adapt this by using a different interval.
Adapt this by using the other particle.
Another (longer) way to approach this question is to find where the particle changes direction by finding where the velocity changes from negative to positive and/or vice versa (i.e., the local extreme values). Then find the distanced traveled on each part of the “trip,” and add or subtract. This will reinforce a lot of the concepts involved in linear motion; that is why it is worth doing. As for the exam, integrating the absolute value is the way to go. However, if this were a non-calculator question, then it would have to be done this way. Find a simpler velocity and try it both ways.
To integrate the absolute value by hand, it is necessary to break the interval into subintervals depending on where the velocity is positive or negative. This is the same as the approach in the bullet immediately above. This, too, is worth showing to reinforce the definition of absolute value.

2021 revised as an in-out question.

There was some unhappiness over the fact that the 2021 AB Calculus exam did not have an in-out questions (Rate and Accumulation Type 1). However, this question does have two rates going in opposite directions. So, just to be ornery, I rewrote it as an in-out questions by changing the context and units while keeping the same velocity functions. The point is that the situation tested can be reframed in other ways. Seeing the same thing in different dress may help students concentrate on the calculus involved. Here it is:

A factory processes cement at the rate of $\displaystyle {{v}_{p}}\left( t \right)=\sin \left( {{{t}^{{1.5}}}} \right)$ tons per hour for $\displaystyle 0\le t\le \pi$ hours. At time t = 0 the amount on hand is P = 5 tons.

The factory ships the cement at a rate given by $\displaystyle {{v}_{Q}}\left( t \right)=\left( {t-1.8} \right){{1.25}^{t}}$ tons per hour for $\displaystyle 0\le t\le \pi$ hours. At time t = 0 the amount shipped is 10 tons.

Find the amount processed and the amount shipped after hour.
Is the amount on hand increasing or decreasing at time t = 1? Explain your reasoning.
At what rate is the rate at which the cement is being shipped changing at t = 1? Is the amount being shipped increasing or decreasing at t = 1? Explain your reasoning.
Find the total amount of cement processed over the time interval $\displaystyle 0\le t\le \pi$ .

Next week 2021 AB 3/ BC 3.

I would be happy to hear your ideas for other ways to use this questions. Please use the reply box below to share your ideas.

Adapting 2021 AB 1 / BC 1

Posted on June 22, 2021 by Lin McMullin

First of nine. One of the things many successful AP Calculus teachers do is to use past AP exam questions throughout the year. Individual multiple-choice exam questions are used as the topics they test are taught; free-response questions are adapted and expanded. There are several ways to do this:

Assign parts of a free-response (FR) question as is as the topic it tests is taught. Later, other parts from the same stem can be assigned. Including previously assigned parts is a spiraling technique. Once students see that you are doing this, they will be more likely to keep up to date on past topics.
Adapting and expanding the questions is another way to use FR questions.

This summer I will be discussing how to do just that. Each week I will look at one of the released 2021 FR questions and suggest how to expand and adapt it. Each stem allows for many more questions than can be asked on any one exam. You have the luxury of asking other things based on the same stem.

This summer’s series of posts will take one question at a time discuss it and suggest additional questions or explorations that may be asked. I will not be presenting solutions. They are available on AP Community bulletin board here and here. I will link the posts to the scoring standards when they are published.

2021 AB 1 / BC 1

This is a Reimann sum and Table question (Type 5) and covers topics from Units 6 and 8 from the current Course and Exam Description. All four parts are fairly typical for this type of problem. There is a little twist in part (b). The context is the density of bacteria growing in a petri dish.

Density is not listed in the Course and Exam Description. It is not covered well in many textbooks. Since it is not listed you need not teach it; exam questions referencing density have enough included information so that a student who has never seen the concept will still be able to answer the question. Keep this in mind as you look at each part; help your students see past the context and look at the calculus. More information on density see these posts Density Functions, and Good Question 15 and Good Question 16.

The stem for 2021 AB 1 / BC 1 reads:

Part (a): Students were asked to estimate the value of the derivative of f at r = 2.25 and explain its meaning, including units, in the context of the problem. The expected procedure is to find the slope between the two values closest to r =2.25. The interpretation is the increase in density as you move away from the center. The units are milligrams per square centimeter per centimeter distant from the center $\frac{{mg/c{{m}^{2}}}}{{cm}}$ .

Discussion and ideas for adapting this question:

AP exams have always asked this question at a value exactly half-way between two values in the table. You may change this to some other place such as r = 3 or r = 0.8.
Units of the derivative are always the units of the function divided by the units of the independent variable. Be sure your students understand this.
The units can be correctly written as $\frac{{mg}}{{c{{m}^{3}}}}$ , but here is a good change to discuss what the units mean. Why does “milligrams per square centimeter per centimeter distant from the center” make more sense?
Ask “Is there a point in the interval [2, 2.5] where the slope of the tangent line is 8? Justify your answer.” This makes use of the Mean Value Theorem.

Part (b) : As usual in this type of problem, students are asked to write a Riemann sum based on the intervals in the table. The difference here is that the integral being approximated, $\displaystyle 2\pi \int_{0}^{4}{{rf\left( r \right)}}dr$ , has an “extra” factor of r in it.

Discussion and ideas for adapting this question:

The question asked for a right Riemann sum. You can easily adapt this by asking for a left Riemann sum, a midpoint Riemann sum, and/or a Trapezoidal approximation.
You may ask for a Riemann sum without the “extra” factor.
You may find a different Riemann sum problem and include an “extra” factor in it.
The integral is the integral for a radial density function. See the Density blog post cited above, example 2.
The radial density function looks like the integral for finding volumes by the method of cylindrical shells. This is more than a coincidence. Why?

Part (c): This part asked if the answer in (b) is an overestimate or an underestimate, with an explanation. For any approximation, some idea of its accuracy is important. In BC questions on power series approximations, a numerical estimate of the error bound is a common question.

Discussion and ideas for adapting this question:

Ask the same question for a different Riemann sum (left, midpoint, trapezoid).
The error in right and left Riemann sums estimates depend on whether the function is increasing or decreasing, and therefore on the first derivative. Midpoint and Trapezoidal approximation estimates are related to the concavity and therefore to the second derivative. See: Good Question 4)
A visual idea helps keep all this straight. Draw sketches showing the Riemann sum rectangles or trapezoids. Whether they lie above or below the graph of the function determines whether the approximation is an overestimate or underestimate.

Part (d): Typical of the Riemann sum table question is the final part with a related question based on a function and not based on the table.

Discussion and ideas for adapting this question:

This is a calculator allowed question. Students should not try to do the integration by hand.
The question asked for the average value of the function on an interval. Other questions you could ask are find the rate of change (derivative) at a point, the total mass $\int_{1}^{4}{{rf\left( r \right)}}dr$ (note “extra” r), the average rate of change on an interval, etc.

Next week 2021 AB 2.

I would be happy to hear your ideas for other ways to use these questions. Please use the reply box below to share your ideas.

Polar Equations for AP Calculus

Posted on January 26, 2021 by Lin McMullin

A recent thread on the AP Calculus Community bulletin boards concerned polar equations. One teacher observed that her students do not have a very solid understanding of polar graphs when they get to calculus. I expect this is a common problem. While ideally the polar coordinate system should be a major topic in pre-calculus courses, this is sometimes not the case. Some classes may even omit the topic entirely. Getting accustomed to a new coordinate scheme and a different way of graphing is a challenge. I remember not having that good an understanding myself when I entered college (where first-year calculus was a sophomore course). Seeing an animated version much later helped a lot.

This blog post will discuss the basics of polar equations and their graphs. It will not be as much as students should understand, but I hope the basics discussed here will be a help. There are also some suggestions for extending the study of polar function as the end.

Instead of using the Cartesian approach of giving every point in the plane a “name” by giving its distance from the y-axis and the x-axis as an ordered pair (x,y), polar coordinates name the point differently. Polar coordinates use the ordered pair (r, θ), where r, gives the distance of the point from the pole (the origin) as a function of θ, the angle that the ray from the pole (origin) to the point makes with the polar axis, (the positive half of the x-axis).

Start with this Desmos graph. It will help if you open it and follow along with the discussion below. The equation in the example is $\displaystyle r(\theta )=2+4\sin (\theta )$ You may change this to explore other graphs. (Because of the way Desmos graphs, you cannot have a slider for θ; the a-slider will move the line and the point on the graph. r(a) gives the value of r(θ).

Notice that as the angle changes the point at varying distance from the pole traces a curve.
Move the slider to π/6. Since sin(π/6) = 0.5, r(π/6) = 4. The red dot is at the point (4, π/6). Move the slider to other points to see how they work. For example, θ = π/2 gives the point (6,π/2).
When the slider gets to θ = 7π/6, r = 0 and the point is at the pole. After this the values of r are negative, and the point is now on the ray opposite to the ray pointing into the third and fourth quadrants. The dashed line turns red to remind you of this.
As we continue around, the point returns to the origin at θ = 11π/6, then values are again positive.
The graph returns to its starting point when θ = 2π. Note (2,0) is the same point as (2, 2π).
Even though this is the graph of a function, some points may be graphed more than once and the vertical line test does not apply.
If we continued around, the graph will retrace the same path. This often happens when the polar function contains trig functions with integer multiples of θ.
- This does not usually happen if no trig functions are involved – try the spiral r = θ.
- If you enter non-integer multiples of θ and extend the domain to large values, vastly different graphs will appear, often making nice designs. Try $\displaystyle r\left( \theta \right)=2+4\sin \left( {1.3\theta } \right)$ for $\displaystyle 0\le \theta \le 20\pi$ . This is an area for exploration (if you have time).

In pre-calculus courses several families of polar graphs are often studied and named. For example, there are cardioids, rose curves, spirals, limaçons, etc. The AP Exams do not refer to these names and students are not required to know the names. The exception is circles which have the following forms where R is the radius: θ=R, r = Rsin(θ) or r = Rsin(θ)

To change from polar to rectangular for use the equations $x=r\cos \left( \theta \right)$ and $y=r\sin \left( \theta \right)$ . This is simple right triangle trigonometry (draw a perpendicular from the point to the x-axis and from there to the pole).

To change from rectangular to polar form use $r=\sqrt{{{{x}^{2}}+{{y}^{2}}}}$ and $\displaystyle \theta =\arctan \left( {\tfrac{y}{x}} \right)$

AP Calculus Applications

There are two applications that are listed on the AP Calculus Course and Exam Description: using and interpreting the derivative of polar curves (Unit 9.7) and finding the area enclosed by a polar curve(s) (Units 9.8 and 9.9).

Since calculus is concerned with motion, AP Students should be able to analyze polar curves for how things are changing:

The rate of change of r away from or towards the pole is given by $\displaystyle \frac{{dr}}{{d\theta }}$
The rate of change of the point with respect to the x-direction is given by $\displaystyle \frac{{dx}}{{d\theta }}$ where $\displaystyle x=r\cos \left( \theta \right)$ from above.
The rate of change of the point with respect to the y-direction is given by $\displaystyle \frac{{dy}}{{d\theta }}$ where $\displaystyle y=r\sin \left( \theta \right)$ from above.
The slope of the tangent line at a point on the curve is $\displaystyle \frac{{dy}}{{dx}}=\frac{{dy/d\theta }}{{dx/d\theta }}$ . See 2018 BC5 (b)

Area

$\displaystyle \underset{{\Delta \theta \to 0}}{\mathop{{\lim }}}\,\sum\limits_{{i=1}}^{\infty }{{\tfrac{1}{2}}}{{r}_{i}}^{2}\Delta \theta =\tfrac{1}{2}\int_{{{{\theta }_{1}}}}^{{{{\theta }_{2}}}}{{{{r}^{2}}d\theta }}$

CAUTION: In using this formula, we need to be careful that the curve does not overlap itself. In the Desmos example, the smaller loop overlaps the larger loop; integrating from 0 to 2π counts the inner loop twice. Notice how this is handled by considering the limits of integration dividing the region into non-overlapping regions:

The area of the outer loop is $\displaystyle \tfrac{1}{2}\int_{{-\pi /6}}^{{7\pi /6}}{{{{{(2+4\sin (\theta ))}}^{2}}d\theta }}\approx 35.525$
The area of the inner loop is $\displaystyle \tfrac{1}{2}\int_{{7\pi /6}}^{{11\pi /6}}{{{{{(2+4\sin (\theta ))}}^{2}}d\theta }}\approx 2.174$
Integrating over the entire domain gives the sum of these two: $\displaystyle \tfrac{1}{2}\int_{0}^{{2\pi }}{{{{{(2+4\sin (\theta ))}}^{2}}d\theta }}=12\pi \approx 37.699$ . This is not the correct area of either part.

This problem can be avoided by considering the geometry before setting up the integral: make sure the areas do not overlap. Restricting r to only non-negative values is often required by the fine print of the theorem in textbooks, but this restriction is not necessary when finding areas and makes it difficult to find, say, the area of the smaller inner loop of the example. Here is another example:

$\displaystyle r\left( \theta \right)=\cos \left( {3\theta } \right)$ . Between 0 and $\displaystyle 2\pi$ this curve traces the same path twice.

Infinite Sequences and Series – Unit 10

Posted on January 19, 2021 by Lin McMullin

Unit 10 covers sequences and series. These are BC only topics (CED – 2019 p. 177 – 197). These topics account for about 17 – 18% of questions on the BC exam.

Topics 10.1 – 10.2

Topic 10.1: Defining Convergent and Divergent Series.

Topic 10. 2: Working with Geometric Series. Including the formula for the sum of a convergent geometric series.

Topics 10.3 – 10.9 Convergence Tests

The tests listed below are tested on the BC Calculus exam. Other methods are not tested. However, teachers may include additional methods.

Topic 10.3: The n^th Term Test for Divergence.

Topic 10.4: Integral Test for Convergence. See Good Question 14

Topic 10.5: Harmonic Series and p-Series. Harmonic series and alternating harmonic series, p-series.

Topic 10.6: Comparison Tests for Convergence. Comparison test and the Limit Comparison Test

Topic 10.7: Alternating Series Test for Convergence.

Topic 10.8: Ratio Test for Convergence.

Topic 10.9: Determining Absolute and Conditional Convergence. Absolute convergence implies conditional convergence.

Topics 10.10 – 10.12 Taylor Series and Error Bounds

Topic 10.10: Alternating Series Error Bound.

Topic 10.11: Finding Taylor Polynomial Approximations of a Function.

Topic 10.12: Lagrange Error Bound.

Topics 10.13 – 10.15 Power Series

Topic 10.13: Radius and Interval of Convergence of a Power Series. The Ratio Test is used almost exclusively to find the radius of convergence. Term-by-term differentiation and integration of a power series gives a series with the same center and radius of convergence. The interval may be different at the endpoints.

Topic 10.14: Finding the Taylor and Maclaurin Series of a Function. Students should memorize the Maclaurin series for $\displaystyle \frac{1}{{1-x}}$ , sin(x), cos(x), and e^x.

Topic 10.15: Representing Functions as Power Series. Finding the power series of a function by, differentiation, integration, algebraic processes, substitution, or properties of geometric series.

Timing

The suggested time for Unit 9 is about 17 – 18 BC classes of 40 – 50-minutes, this includes time for testing etc.

Previous posts on these topics:

Before sequences

Amortization Using finite series to find your mortgage payment. (Suitable for pre-calculus as well as calculus)

A Lesson on Sequences An investigation, which could be used as early as Algebra 1, showing how irrational numbers are the limit of a sequence of approximations. Also, an introduction to the Completeness Axiom.

Everyday Series

Convergence Tests

Reference Chart

Which Convergence Test Should I Use? Part 1 Pretty much anyone you want!

Which Convergence Test Should I Use? Part 2 Specific hints and a discussion of the usefulness of absolute convergence

Good Question 14 on the Integral Test

Sequences and Series

Graphing Taylor Polynomials Graphing calculator hints

Introducing Power Series 1

Introducing Power Series 2

Introducing Power Series 3

New Series from Old 1 substitution (Be sure to look at example 3)

New Series from Old 2 Differentiation

New Series from Old 3 Series for rational functions using long division and geometric series

Geometric Series – Far Out An instructive “mistake.”

A Curiosity An unusual Maclaurin Series

Synthetic Summer Fun Synthetic division and calculus including finding the (finite)Taylor series of a polynomial.

Error Bounds

Error Bounds Error bounds in general and the alternating Series error bound, and the Lagrange error bound

The Lagrange Highway The Lagrange error bound.

What’s the “Best” Error Bound?

Review Notes

Type 10: Sequences and Series Questions

Parametric Equations, Polar Coordinates, and Vector-Valued Functions – Unit 9

Posted on January 12, 2021 by Lin McMullin

Unit 9 includes all the topics listed in the title. These are BC only topics (CED – 2019 p. 163 – 176). These topics account for about 11 – 12% of questions on the BC exam.

Comments on Prerequisites: In BC Calculus the work with parametric, vector, and polar equations is somewhat limited. I always hoped that students had studied these topics in detail in their precalculus classes and had more precalculus knowledge and experience with them than is required for the BC exam. This will help them in calculus, so see that they are included in your precalculus classes.

Topics 9.1 – 9.3 Parametric Equations

Topic 9.1: Defining and Differentiation Parametric Equations. Finding dy/dx in terms of dy/dt and dx/dt

Topic 9.2: Second Derivatives of Parametric Equations. Finding the second derivative. See Implicit Differentiation of Parametric Equations this discusses the second derivative.

Topic 9.3: Finding Arc Lengths of Curves Given by Parametric Equations.

Topics 9.4 – 9.6 Vector-Valued Functions and Motion in the plane

Topic 9.4 : Defining and Differentiating Vector-Valued Functions. Finding the second derivative. See this A Vector’s Derivatives which includes a note on second derivatives.

Topic 9.5: Integrating Vector-Valued Functions

Topic 9.6: Solving Motion Problems Using Parametric and Vector-Valued Functions. Position, Velocity, acceleration, speed, total distance traveled, and displacement extended to motion in the plane.

Topics 9.7 – 9.9 Polar Equation and Area in Polar Form.

Topic 9.7: Defining Polar Coordinate and Differentiation in Polar Form. The derivatives and their meaning.

Topic 9.8: Find the Area of a Polar Region or the Area Bounded by a Single Polar Curve

Topic 9.9: Finding the Area of the Region Bounded by Two Polar Curves. Students should know how to find the intersections of polar curves to use for the limits of integration.

Timing

The suggested time for Unit 9 is about 10 – 11 BC classes of 40 – 50-minutes, this includes time for testing etc.

Previous posts on these topics :

Parametric Equations

Vector Valued Functions

Polar Form

Applications of Integration – Unit 8

Posted on November 17, 2020 by Lin McMullin

I haven’t missed Unit 7! This unit seems to fit more logically after the opening unit on integration (Unit 6). The Course and Exam Description (CED) places Unit 7 Differential Equations before Unit 8 probably because the previous unit ended with techniques of antidifferentiation. My guess is that many teachers will teach Unit 8: Applications of Integration immediately after Unit 6 and before Unit 7: Differential Equations. The order is up to you. Unit 7 will post next Tuesday.

Unit 8 includes some standard problems solvable by integration (CED – 2019 p. 143 – 161). These topics account for about 10 – 15% of questions on the AB exam and 6 – 9% of the BC questions.

Topics 8.1 – 8.3 Average Value and Accumulation

Topic 8.1 Finding the Average Value of a Function on an Interval Be sure to distinguish between average value of a function on an interval, average rate of change on an interval and the mean value

Topic 8.2 Connecting Position, Velocity, and Acceleration of Functions using Integrals Distinguish between displacement (= integral of velocity) and total distance traveled (= integral of speed)

Topic 8. 3 Using Accumulation Functions and Definite Integrals in Applied Contexts The integral of a rate of change equals the net amount of change. A really big idea and one that is tested on all the exams. So, if you are asked for an amount, look around for a rate to integrate.

Topics 8.4 – 8.6 Area

Topic 8.4 Finding the Area Between Curves Expressed as Functions of x

Topic 8.5 Finding the Area Between Curves Expressed as Functions of y

Topic 8.6 Finding the Area Between Curves That Intersect at More Than Two Points Use two or more integrals or integrate the absolute value of the difference of the two functions. The latter is especially useful when do the computation of a graphing calculator.

Topics 8.7 – 8.12 Volume

Topic 8.7 Volumes with Cross Sections: Squares and Rectangles

Topic 8.8 Volumes with Cross Sections: Triangles and Semicircles

Topic 8.9 Volume with Disk Method: Revolving around the x– or y-Axis Volumes of revolution are volumes with circular cross sections, so this continues the previous two topics.

Topic 8.10 Volume with Disk Method: Revolving Around Other Axes

Topic 8.11 Volume with Washer Method: Revolving Around the x– or y-Axis See Subtract the Hole from the Whole for an easier way to remember how to do these problems.

Topic 8.12 Volume with Washer Method: Revolving Around Other Axes. See Subtract the Hole from the Whole for an easier way to remember how to do these problems.

Topic 8.13 Arc Length BC Only

Topic 8.13 The Arc Length of a Smooth, Planar Curve and Distance Traveled BC ONLY

Timing

The suggested time for Unit 8 is 19 – 20 classes for AB and 13 – 14 for BC of 40 – 50-minute class periods, this includes time for testing etc.

Previous posts on these topics for both AB and BC include:

Average Value and Accumulation

Average Value of a Function and Average Value of a Function

Half-full or Half-empty

Accumulation: Need an Amount?

AP Accumulation Questions

Good Question 7 – 2009 AB 3 Accumulation, explain the meaning of an integral in context, unit analysis

Good Question 8 – or Not Unit analysis

Graphing with Accumulation 1 Seeing increasing and decreasing through integration

Graphing with Accumulation 2 Seeing concavity through integration

Area

Area Between Curves

Under is a Long Way Down Avoiding “negative area.”

Improper Integrals and Proper Areas BC Topic

Math vs. the “Real World” Improper integrals BC Topic

Volume

Volumes of Solids with Regular Cross-sections

Volumes of Revolution

Why You Never Need Cylindrical Shells

Visualizing Solid Figures 1

Visualizing Solid Figures 2

Visualizing Solid Figures 3

Visualizing Solid Figures 4

Visualizing Solid Figures 5

Painting a Point

Subtract the Hole from the Whole and Does Simplifying Make Things Simpler?

Other Applications of Integrals

Density Functions have been tested in the past, but are not specifically listed on the CED then or now.

Who’d a Thunk It? Some integration problems suitable for graphing calculator solution

Here are links to the full list of posts discussing the ten units in the 2019 Course and Exam Description.

2019 CED – Unit 1: Limits and Continuity

2019 CED – Unit 2: Differentiation: Definition and Fundamental Properties.

2019 CED – Unit 3: Differentiation: Composite , Implicit, and Inverse Functions

2019 CED – Unit 4 Contextual Applications of the Derivative Consider teaching Unit 5 before Unit 4

2019 – CED Unit 5 Analytical Applications of Differentiation Consider teaching Unit 5 before Unit 4

2019 – CED Unit 6 Integration and Accumulation of Change

2019 – CED Unit 7 Differential Equations Consider teaching after Unit 8

2019 – CED Unit 8 Applications of Integration Consider teaching after Unit 6, before Unit 7

2019 – CED Unit 9 Parametric Equations, Polar Coordinates, and Vector-Values Functions

2019 CED Unit 10 Infinite Sequences and Series

Riemann Sum & Table Problems (Type 5)

Posted on March 17, 2020 by Lin McMullin

AP Questions Type 5: Riemann Sum & Table Problems

Tables may be used to test a variety of ideas in calculus including analysis of functions, accumulation, theory and theorems, and position-velocity-acceleration, among others. Numbers and working with numbers is part of the Rule of Four and table problems are one way this is tested. This question often includes an equation in a latter part of the problem that refers to the same situation.

What students should be able to do:

Find the average rate of change over an interval
Approximate the derivative using a difference quotient. Use the two values closest to the number at which you are approximating. This amounts to finding the slope or rate of change. Show the quotient even if you can do the arithmetic in your head and even if the denominator is 1.
Use a left-, right-, or midpoint- Riemann sums or a trapezoidal approximation to approximate the value of a definite integral using values in the table (typically with uneven subintervals). The Trapezoidal Rule, per se, is not required; it is expected that students will add the areas of a small number of trapezoids without reference to a formula.
Average value, average rate of change, Rolle’s theorem, the Mean Value Theorem and the Intermediate Value Theorem. (See 2007 AB 3 – four simple parts that could be multiple-choice questions; the mean on this question was 0.96 out of a possible 9.)
These questions are usually presented in some context and answers should be in that context. The context may be something growing (changing over time) or linear motion.
Use the table to find a value based on the Mean Value Theorem (2018 AB 4(b)) or Intermediate Value Theorem.
One of the parts of this question asks a related question based on a function given by an equation.
Unit analysis.

Do’s and Don’ts

Do: Remember that you do not know what happens between the values in the table unless some other information is given. For example, do not assume that the largest number in the table is the maximum value of the function, or that the function is decreasing between two values just because a value is less than the preceding value.

Do: Show what you are doing even if you can do it in your head. If you’re finding a slope, show the quotient even if the denominator is 1.

Do Not do arithmetic: A long expression consisting entirely of numbers such as you get when doing a Riemann sum, does not need to be simplified in any way. If you a simplify correct answer incorrectly, you will lose credit.

Do Not leave expression such as R(3) – pull its numerical value from the table.

Do Not: Find a regression equation and then use that to answer parts of the question. While regression is perfectly good mathematics, regression equations are not one of the four things students may do with their calculator. Regression gives only an approximation of our function. The exam is testing whether students can work with numbers.

This question typically covers topics from Unit 6 of the 2019 CED but may include topics from Units 2, 3, and 4 as well.

Free-response examples:

2007 AB 3 (4 simple parts on various theorems, yet the mean score was 0.96 out of 9),
2017 AB 1/BC 1, and AB 6,
2016 AB 1/BC 1
2018 AB 4

Multiple-choice questions from non-secure exams:

2012 AB 8, 86, 91
2012 BC 8, 81, 86 (81 and 86 are the same on both the AB and BC exams)

Revised March 12, 2021

Teaching Calculus

The pleasure lies not in discovering the truth, but in searching for it.

Category Archives: Integration Applications

Adapting 2021 AB 2

2021 AB 2

Adapting 2021 AB 1 / BC 1

2021 AB 1 / BC 1

Polar Equations for AP Calculus