Category Archives: Integration Theory

Getting Ready to Integrate

Posted on by
Reply

Behind every definite integral is a Riemann sums. Students need to know about Riemann sums so that they can understand definite integrals (a shorthand notation for the limit if a Riemann sum) and the Fundamental theorem of Calculus. Theses posts help prepare students for Riemann sums.

Integration Itinerary  Some thoughts on the order of topics in your integration unit.

Some preliminary posts leading up to Riemann sums

  1. The Old Pump Where I start Integration
  2. Flying into Integrationland Continues the investigation in the Old Pump – the airplane problem
  3. Jobs, Jobs, Jobs Integration in real life.
  4. Working Towards Riemann Sums (12-10-2012)

While I prefer to teach antidifferentiation after students have learned about the Fundamental Theorem of Calculus, others prefer to discuss antidifferentiation firsts and the topic often precedes Riemann sums in textbooks. (See Integration Itinerary )  If you are among those, here are posts on antidifferentiation. If you teach this topic later, save this post for then.

ANTIDIFFERENTIATION

Antidifferentiation  (11-28-2012)

Why Muss with the “+C”? But still don’t forget it.

Arbitrary Ranges (2-9-2014) Integrating inverse trigonometric functions.

ANTIDIFFERENTIATION BY PARTS This is a BC topic, or you could use it after the exam in an AB course.

Integration by Parts 1 (2-2-2013) Basics

Integration by Parts 2 (2-4-2013) The Tabular Method

Modified Tabular Integration (7-24-2013) A quicker way

Parts and More Parts (8-5-2016) Reduction formulas (Not tested on the AP Calculus exams)

Good Question 12 – Parts with a Constant (12-13-2016) How come you don’t need the “+C”?

 

 

 

 

Good Question 15: 2018 BC 2(a)

Posted on by
Reply

My choices for the Good Question series are somewhat eclectic. Some are chosen because they are good, some because they are bad, some because I learned something from them, some because they can be extended, and some because they can illustrate some point of mathematics. This question and the next, Good Question 16, are in the latter group. They both concern units. They both are taken from this year’s AP calculus BC exam; both are suitable for AB classes. In this question 2018 BC 2(a) has some unusual units and in the next 2018 BC 2(b) the units help you figure out what to do. Part (c) concerns an improper integral and pard (d) is about parametric equation, neither of these are AB topics. 

2018 BC 2(a)

2018 BC 2 gave an equation that modeled the density p(h) of plankton in a sea in units of millions of cells per cubic meter, as a function of the depth, h, in meters.  Specifically, p\left( h \right)=0.2{{h}^{2}}{{e}^{{-0.0025{{h}^{2}}}}} for 0\le h\le 30. Part (a) asked for the value of {p}'\left( {25} \right) and also asked students “Using correct units, [to] interpret the meaning of {p}'\left( {25} \right) in the context of the problem.”

Plankton

This was a calculator active question, so the computation is easy enough: {p}'\left( {25} \right)=-1.17906

Now units of the derivative are always very easy to determine; this should be automatic. The derivative is the limit of a difference quotient, so its units are the units of the numerator divided by the units of the denominator. In this case that’s millions of cells per cubic meter per meter of depth.

While “millions of cells per meter to the fourth power” is technically correct and will probably earn credit, what is a meter to the fourth power?

It is similar to the better-known situation with velocity and acceleration. I never liked the idea of saying the acceleration is so many meters per square second. What’s a square second? Are there round seconds? Acceleration is the change in velocity in meters per second per second; that is, at a particular time the velocity is changing at the rate of so-many meters per second each second. 

Returning to the question, a cubic meter (volume) and a meter of depth (linear) are not things that you should combine. The notational convenience of writing meters to the fourth power hides the true meaning. So, a better interpretation is “At depth of  25 meters, the number cells is decreasing at the rate of 1.179 million cells per cubic meter per meter of depth.” or “The number of cells changing at the rate of -1.179 million cells per cubic meter per meter of depth.”

Had the model been given using volume units such as millions of cells per liter, then the units of the derivative would be millions of cells per liter per meter. That makes more sense.

But what does it mean?

Let’s look at the graph of the derivative. The window is 0 < h < 30 and –2.5 < p(x) < 2.5

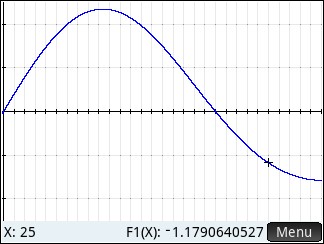
It means, that as we pass thru that thin (thickness \Delta h\to 0) film of water 25 meters down, there are approximately 1.179 million cells per cubic meter less than in the thin film right above it and more than in the thin film right below it.

For reference, p\left( {25} \right)\approx 26.2014 million cells per cubic meter. Of course, that thin (thickness \Delta h\to 0) film of water has very little volume; it is kind of difficult to think of a cubic meter exactly 25 meters below the surface (maybe a cube extending from 24.5 meters to 25.5 meters?). As \Delta h\to 0 does a cubic meter approach a square meter?

The cubic meter above h = 25 has \displaystyle \int_{{24}}^{{25}}{{p\left( h \right)(1)dh}}=26.763 cells and the cubic meter below has 25.586 million cells. This is a decrease of 1.1767 million cells. So, the derivative is reasonable.

(To make the units of 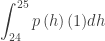\displaystyle \int_{{24}}^{{25}}{{p\left( h \right)(1)dh}} correct, I included a factor of 1 square meter, this multiplied by p(h) million cells per cubic meter and by dh in meters give a result of millions of cells. More on why this is necessary in Good Question 16 on density.)

Previous Good Questions can be found under the “Thru the Year” tab on the black navigation bar at the top of the page, or here.

Units

Posted on by
Reply

I had a question from a reader recently asking about how to determine the units for derivatives and integrals.

Derivatives: The units of the derivative are the units of dy divided by the units of dx, or the units of the dependent variable (f(x) or y) divided by the units of the independent variable (x). The reason for this comes from the definition of the derivative:

\displaystyle {f}'\left( x \right)=\underset{{\Delta x\to 0}}{\mathop{{\lim }}}\,\frac{{f\left( {x+\Delta x} \right)-f\left( x \right)}}{{\Delta x}}

In the quotient the numerator has the units of f and in the denominator the has the same units as x.

Definite Integrals: The units of a definite integral are the units of the integrand f(x) multiplied by the units of dx. This comes directly from the definition of a definite integral:

\displaystyle \int_{a}^{b}{{f\left( x \right)dx}}=\underset{{n\to \infty }}{\mathop{{\lim }}}\,\sum\limits_{{i=1}}^{n}{{f\left( {{{x}_{i}}^{*}} \right)\frac{{b-a}}{n}}}

The factor (b – a) has the same units a x, the independent variable, and the f(x) has whatever units it has. From the Riemann sum we can see that since these factors are multiplied, that product is the units of the definite integral.

The integrand is the derivative of its antiderivative (by the FTC) and so its units are often derivative units (miles per hour, furlongs per fortnight, etc.). When multiplied by (b – a)/n its units “cancel” the units of the denominator of f(x) and the result is the units of the numerator of f(x).  This is not always the case*, therefore, multiplying the units is safest.

*The definite integral \displaystyle \int_{{-2}}^{2}{{\sqrt{{4-{{x}^{2}}}}dx}} gives the area of a semi-circle of radius 2 feet. The units of the radical are feet and represent the vertical distance from the x-axis to a point in the semi-circle; the dx is the horizontal side of the Riemann sum rectangles also in feet. Both are measured in the same linear units and the area is their product: feet times feet or square feet.

 

 

 

 

 

Good Question 13

Posted on by
Reply

Let’s end the year with this problem that I came across a while ago in a review book:

Integrate \int{x\sqrt{x+1}dx}

It was a multiple-choice question and had four choices for the answer. The author intended it to be done with a u-substitution but being a bit rusty I tried integration by parts. I got the correct answer, but it was not among the choices. So I thought it would make a good challenge to work on over the holidays.

    1. Find the antiderivative using a u-substitution.
    2. Find the antiderivative using integration by parts.
    3. Find the antiderivative using a different u-substitution.
    4. Find the antiderivative by adding zero in a convenient form.

Your answers for 1, 3, and 4 should be the same, but look different from your answer to 2. The difference is NOT due to the constant of integration which is the same for all four answers. Show that the two forms are the same by

  1. “Simplifying” your answer to 2 and get a third form of the answer.
  2. “Simplifying” your answer to 1, 3, 4 and get that third form again.

Give it a try before reading on. The solutions are below the picture.

Method 1: u-substitution

Integrate \int{x\sqrt{x+1}dx}

u=x+1,x=u-1,dx=du

\int{x\sqrt{x+1}dx=}\int{\left( u-1 \right)\sqrt{u}}du=\int{{{u}^{3/2}}-{{u}^{1/2}}}du=\tfrac{5}{2}{{u}^{5/2}}-\tfrac{3}{2}{{u}^{3/2}}

\tfrac{2}{5}{{\left( x+1 \right)}^{5/2}}-\tfrac{2}{3}{{\left( x+1 \right)}^{3/2}}+C

Method 2: By Parts

Integrate \int{x\sqrt{x+1}dx}

u=x,du=dx

dv=\sqrt{x+1}dx,v=\tfrac{2}{3}{{\left( x+1 \right)}^{3/2}}

\int{x\sqrt{x+1}dx}=\tfrac{2}{3}x{{\left( x+1 \right)}^{3/2}}-\int{\tfrac{2}{3}{{\left( x+1 \right)}^{3/2}}dx}=

\tfrac{2}{3}x{{\left( x+1 \right)}^{3/2}}-\tfrac{4}{15}{{\left( x+1 \right)}^{5/2}}+C

Method 3: A different u-substitution

Integrate \int{x\sqrt{x+1}dx}

u=\sqrt{x+1},x={{u}^{2}}-1,

du=\tfrac{1}{2}{{\left( x+1 \right)}^{-1/2}}dx,dx=2udu

2{{\int{\left( {{u}^{2}}-1 \right){{u}^{2}}}}^{{}}}du=2\int{{{u}^{4}}-{{u}^{2}}}du=\tfrac{2}{5}{{u}^{5}}-\tfrac{2}{3}{{u}^{3}}=

\tfrac{2}{5}{{\left( x+1 \right)}^{5/2}}-\tfrac{2}{3}{{\left( x+1 \right)}^{3/2}}+C

This gives the same answer as Method 1.

Method 4: Add zero in a convenient form.

Integrate \int{x\sqrt{x+1}dx}

\int{x\sqrt{x+1}}dx=\int{x\sqrt{x+1}+\sqrt{x+1}-\sqrt{x+1} dx=}

\int{\left( x+1 \right)\sqrt{x+1}-\sqrt{x+1}}dx=

\int{{{\left( x+1 \right)}^{3/2}}-{{\left( x+1 \right)}^{1/2}}dx}=

\tfrac{2}{5}{{\left( x+1 \right)}^{5/2}}-\tfrac{2}{3}{{\left( x+1 \right)}^{3/2}}+C

This, also, gives the same answer as Methods 1 and 3.

So, by a vote of three to one Method 2 must be wrong. Yes, no, maybe?

No, all four answers are the same. Often when you get two forms for the same antiderivative, the problem is with the constant of integration. That is not the case here. We can show that the answers are the same by factoring out a common factor of {{\left( x+1 \right)}^{3/2}}. (Factoring the term with the lowest fractional exponent often is the key to simplifying expressions of this kind.)

Simplify the answer for Method 2:

\tfrac{2}{3}x{{\left( x+1 \right)}^{3/2}}-\tfrac{4}{15}{{\left( x+1 \right)}^{5/2}}+C=

\tfrac{2}{3}{{\left( x+1 \right)}^{3/2}}\left( x-\tfrac{2}{5}\left( x+1 \right) \right)+C=

\displaystyle \tfrac{2}{3}{{\left( x+1 \right)}^{3/2}}\left( \frac{5x-2x-2}{5} \right)+C=

\tfrac{2}{15}{{\left( x+1 \right)}^{3/2}}\left( 3x-2 \right)+C

Simplify the answer for Methods 1, 3, and 4:

\tfrac{2}{5}{{\left( x+1 \right)}^{5/2}}-\tfrac{2}{3}{{\left( x+1 \right)}^{3/2}}+C=

\tfrac{2}{15}{{\left( x+1 \right)}^{3/2}}\left( 3\left( x+1 \right)-5 \right)+C=

\tfrac{2}{15}{{\left( x+1 \right)}^{3/2}}\left( 3x-2 \right)+C

So, same answer and same constant.

Is this a good question? No and yes.

As a multiple-choice question, no, this is not a good question. It is reasonable that a student may use the method of integration by parts. His or her answer is not among the choices, but they have done nothing wrong. Obviously, you cannot include both answers, since then there will be two correct choices. Moral: writing a multiple-choice question is not as simple as it seems.

From another point of view, yes, this is a good question, but not for multiple-choice. You can use it in your class to widen your students’ perspective. Give the class a hint on where to start. Even better, ask the class to suggest methods; if necessary, suggest methods until you have all four (… maybe there is even a fifth). Assign one-quarter of your class to do the problem by each method. Then have them compare their results. Finally, have them do the simplification to show that the answers are the same.

My next post will be after the holidays.

Happy Holidays to Everyone!

.

Starting Integration

Posted on by
Reply

Behind every definite integral is a Riemann sums. Students need to know about Riemann sums so that they can understand definite integrals (a shorthand notation for the limit if a Riemann sun) and the Fundamental theorem of Calculus. Theses posts help prepare students for Riemann sums.

  1. The Old Pump Where I start Integration
  2. Flying into Integrationland Continues the investigation in the Old Pump – the airplane problem
  3. Working Towards Riemann Sums
  4. Definition of the Definite Integral and the FTC – a more exact demonstration from last Friday’s post and The Fundamental Theorem of Calculus –  an older demonstration
  5. More about the FTC The derivative of a function defined by an integral – the other half of the FTC.
  6. Good Question 11 Riemann Reversed – How to find the integral, given the Riemann sum
  7. Properties of Integrals
  8. Variation on a Theme – 2 Comparing Riemann sums
  9. Trapezoids – Ancient and Modern – some history

 

 

 

 

 

The Definite Integral and the FTC

Posted on by
Reply

The Definition of the Definite Integral.

The definition of the definite integrals is: If f is a function continuous on the closed interval [a, b], and a={{x}_{0}}<{{x}_{1}}<{{x}_{2}}<\cdots <{{x}_{{n-1}}}<{{x}_{n}}=b  is a partition of that interval, and x_{i}^{*}\in [{{x}_{{i-1}}},{{x}_{i}}], then

\displaystyle \underset{{\left| {\left| {\Delta x} \right|} \right|\to 0}}{\mathop{{\lim }}}\,\sum\limits_{{i=0}}^{n}{{f\left( {x_{i}^{*}} \right)}}\left( {{{x}_{i}}-{{x}_{{i-i}}}} \right)=\int\limits_{a}^{b}{{f\left( x \right)dx}}

The left side of the definition is, of course, any Riemann sum for the function f on the interval [a, b]. In addition to being shorter, the right side also tells you about the interval on which the definite integral is computed. The expression \left\| {\Delta x} \right\|  is called the “norm of the partition” and is the longest subinterval in the partition. Usually, all the subintervals are the same length, \frac{{b-a}}{n}, and this is the last you will hear of the norm. With all the subdivisions of the same length this can be written as

\displaystyle \underset{{n\to \infty }}{\mathop{{\lim }}}\,\sum\limits_{{i=0}}^{n}{{f\left( {x_{i}^{*}} \right)}}\frac{{b-a}}{n}=\int\limits_{a}^{b}{{f\left( x \right)dx}}

Other than that, there is not much more to the definition. It is simply a quicker and more efficient notation for the sum.

The Fundamental Theorem of Calculus (FTC).

First recall the Mean Value Theorem (MVT) which says: If a function is continuous on the closed interval [a, b] and differentiable on the open interval (a, b) then there exist a number, c, in the open interval (a, b) such that {f}'\left( c \right)\left( {b-a} \right)=f\left( b \right)-f\left( a \right).

Next, let’s rewrite the definition above with a few changes. The reason for this will become clear.

\int\limits_{a}^{b}{{{f}'\left( x \right)dx}}=\underset{{\left| {\left| {\Delta x} \right|} \right|\to 0}}{\mathop{{\lim }}}\,\sum\limits_{{i=0}}^{n}{{{f}'\left( {{{c}_{i}}} \right)\left( {{{x}_{i}}-{{x}_{{i-i}}}} \right)}}

Since every function is the derivative of another function (even though we may not know that function or be able to write a closed-form expression for it), I’ve expressed the function as a derivative, I’ve also chosen the point in each subinterval, {{c}_{i}}, to be the number in each subinterval guaranteed by the MVT for that subinterval.

Then, \displaystyle {f}'\left( {{{c}_{i}}} \right)\left( {{{x}_{i}}-{{x}_{{i-i}}}} \right)=f\left( {{{x}_{i}}} \right)-f\left( {{{x}_{{i-1}}}} \right). Making this substitution, we have

\int\limits_{a}^{b}{{{f}'\left( x \right)dx}}=\underset{{\left| {\left| {\Delta x} \right|} \right|\to 0}}{\mathop{{\lim }}}\,\sum\limits_{{i=0}}^{n}{{\left( {f\left( {{{x}_{i}}} \right)-f\left( {{{x}_{{i-1}}}} \right)} \right)}}

\displaystyle =f\left( {{{x}_{1}}} \right)-f\left( {{{x}_{0}}} \right)+f\left( {{{x}_{2}}} \right)-f\left( {{{x}_{1}}} \right)+f\left( {{{x}_{3}}} \right)-f\left( {{{x}_{2}}} \right)+\cdots +f\left( {{{x}_{n}}} \right)-f\left( {{{x}_{{n-1}}}} \right)

\displaystyle =f\left( {{{n}_{n}}} \right)-f\left( {{{x}_{0}}} \right)

And since {{x}_{0}}=a and  {{x}_{n}}=b,

\displaystyle \int_{a}^{b}{{{f}'\left( x \right)dx}}=f\left( b \right)-f\left( a \right)

This equation is called the Fundamental Theorem of Calculus. In words, it says that the integral of a function can be found by evaluating the function of which the integrand is the derivative at the endpoints of the interval and subtracting the values. This is a number that may be positive, negative, or zero depending on the function and the interval. The function of which the integrand is the derivative, is called the antiderivative of the integrand.

The real meaning and use of the FTC is twofold:

  1. It says that the integral of a rate of change (i.e. a derivative) is the net amount of change. Thus, when you want to find the amount of change – and you will want to do this with every application of the derivative – integrate the rate of change.
  2. It also gives us an easy way to evaluate a Riemann sum without going to all the trouble that is necessary with a Riemann sum; simply evaluate the antiderivative at the endpoints and subtract.

At this point I suggest two quick questions to emphasize the second point:

  1. Find \int_{3}^{7}{{2xdx}}.

Ask if anyone knows a function whose derivative is 2x? Your students will know this one. The answer is x2, so

\displaystyle \int_{3}^{7}{{2xdx}}={{7}^{2}}-{{3}^{2}}=40.

Much easier than setting up and evaluating a Riemann sum!

2. Then ask your students to find the area enclosed by the coordinate axes and the graph of cos(x) from zero to \frac{\pi }{2}. With a little help they should arrive at

\displaystyle \int_{0}^{{\pi /2}}{{\cos \left( x \right)dx}}.

Then ask if anyone knows a function whose derivative is cos(x). it’s sin(x), so

\displaystyle \int_{0}^{{\pi /2}}{{\cos \left( x \right)dx}}=\sin \left( {\frac{\pi }{2}} \right)-\sin \left( 0 \right)=1-0=1.

At this point they should be convinced that the FTC is a good thing to know.

There is another form of the FTC that is discussed in More About the FTC.

Good Question 12 – Parts with a Constant?

Posted on by
Reply

partsSomeone asked me about this a while ago and I thought I would share it with you. It may be a good question to get your students thinking about; see if they can give a definitive answer that will, of course, include a justification.

Integration by Parts is summarized in the equation

\displaystyle \int_{{}}^{{}}{udv}=uv-\int_{{}}^{{}}{vdu}

To use the equation, you choose part of a given integral (left side) to be u and part to be dv, both functions of x. Then you differentiate u and integrate dv and use them on the right side to obtain a simpler integral that you can integrate.

The question is this: When you integrate dv, should you, can you, have a constant of integration, the “+ C ” that you insist upon in other integration problems? Why don’t you use it here? Or can you?

Scroll down for my answer.

Answer: Let’s see what happens if we use a constant. Assume that \displaystyle \int_{{}}^{{}}{dv}=v+C. Then

\displaystyle \int_{{}}^{{}}{udv}=u\cdot \left( v+C \right)-\int_{{}}^{{}}{\left( v+C \right)du}

\displaystyle =uv+Cu-\left( \int_{{}}^{{}}{vdu}+\int_{{}}^{{}}{Cdu} \right)

\displaystyle =uv+Cu-\int_{{}}^{{}}{vdu}-Cu

\displaystyle =uv-\int_{{}}^{{}}{vdu}

So, you may use a constant if you want, but it will always add out of the expression.

For more on integration by parts see here for the basic idea, here for the tabular method, here for a quicker way than the tabular method, and here for more on the tabular method and reduction formulas.