Category Archives: Derivative Applications

Summer Fun

Posted on by
Reply

Every Spring I have a lot of fun proofreading Audrey Weeks’ new Calculus in Motion illustrations for the most recent AP Calculus Exam questions. These illustrations run on Geometers’ Sketchpad. In addition to the exam questions Calculus in Motion (and its companion Algebra in Motion) include separate animations illustrating most of the concepts in calculus and algebra. This is a great resource for your classes.

The proofreading and the cross-country conversations with Audrey give me a chance to learn more about the questions.

This year, I really got into 2018 AB 6, the differential equation question. I wrote an exploration (or as the kids would say “worksheet”) on a function very similar to the differential equation in that question. The exploration, which is rather long, includes these topics:

  • Finding the general solution of the differential equation by separating the variables
  • Checking the solution by substitution
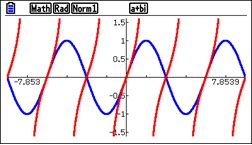
  • Using a graphing utility to explore the solutions for all values of the constant of integration, C
  • Finding the solutions’ horizontal and vertical asymptotes
  • Finding several particular solutions
  • Finding the domains of the particular solutions
  • Finding the extreme value of all solutions in terms of C
  • Finding the second derivative (implicit differentiation)
  • Considering concavity
  • Investigating a special case or two

I also hope that in working through this exploration students will learn not so much about this particular function, but how to use the tools of algebra, calculus, and technology to fully investigate any function and to find all its foibles.

Students will need to have studied calculus through differential equations before they start the exploration. I will repost it next January for them.

The exploration is here for you to try. Try it before you look at the solutions. It will give you something to do over the summer – well not all summer, only an hour or so.

As always, I appreciate your feedback and comments. Please share them with me using the reply box below.

There will be only occasional, very occasional, posts over the Summer. More regular posting will begin again in August. Enjoy the Explorations, and, more important, enjoy the Summer!

.

A Note on Speed

Posted on by
2

A quick note on speed.

The idea of differentiating speed to determine where it is increasing or decreasing is perfectly reasonable.

\displaystyle \text{Speed}=s(t)=\left| {v\left( t \right)} \right|=\sqrt{{{{{\left( {v(t)} \right)}}^{2}}}}. Then,

\displaystyle {s}'\left( t \right)=\frac{{2v\left( t \right){v}'\left( t \right)}}{{2\sqrt{{{{{\left( {v(t)} \right)}}^{2}}}}}}=\frac{{v\left( t \right)a\left( t \right)}}{{\sqrt{{{{{\left( {v(t)} \right)}}^{2}}}}}}

Since the denominator is positive, \displaystyle {s}'\left( t \right)>0 and speed is increasing when \displaystyle v\left( t \right) and \displaystyle a\left( t \right) have the same sign, and \displaystyle {s}'\left( t \right)<0 and speed is decreasing when they have different signs.

As a practical matter, this is the “long way.” It requires you to calculate the sign of the velocity and acceleration and some other stuff. So, the traditional way, without the other stuff, is faster. On the other hand, it carries over nicely to higher dimensions where the velocity and acceleration vectors do not have signs, per se. 

See also a previous post on Speed here.

(This occurred to me in the shower this morning; I don’t think I ever realized it before – TMI.)

Other Derivative Applications

Posted on by
Reply

Some final applications of derivatives

L’Hospital’s Rule 

Locally Linear L’Hospital’s Demonstration of the proof

L’Hospital Rules the Graph

Good Question An AP Exam question that can be used to delve deeper into L’Hospital’s Rule (2008 AB 6)

Related Rate problems

Related Rates Problems 1 

 Related Rate Problems II

Good Question 9  Baseball and Related Rates

Painting a Point  Mostly integration, but with a Related Rate tie-in.

 

 

 

 

 

The Mean Value Theorem

Posted on by
1

Another application of the derivative is the Mean Value Theorem (MVT). This theorem is very important. One of its most important uses is in proving the Fundamental Theorem of Calculus (FTC), which comes a little later in the year. Here are some previous post on the MVT:

Fermat’s Penultimate Theorem   A lemma for Rolle’s Theorem: Any function extreme value(s) on an open interval must occur where the derivative is zero or undefined.

Rolle’s Theorem   A lemma for the MVT: On an interval if a function is continuous on a closed interval [a, b] and differentiable on the open interval (a, b) and f(a) = f(b), there must exist a number c in the open interval (a, b) where f ‘(c) = 0.

Mean Value Theorem I   Proof

Mean Value Theorem II   Graphical Considerations

Darboux’s Theorem   The Intermediate Value Theorem for derivatives.

Mean Tables

 

 

 

 

 

Extreme Values and Linear Motion

Posted on by
Reply

Two more applications of differentiation are finding extreme values and the analysis of linear motion.

Extreme Values

The Marble and the Vase

Extremes without Calculus

A Standard Problem

Far Out!

Linear Motion – Motion on a Line 

Type 2 Problems

Motion Problems: Same Thing, Different Context

The Ubiquitous Particle Motion Problem  – a PowerPoint Presentation and its Handout

Brian Leonard’s Particle Motion Game Velocity Game  and answers Velocity game Answers

Matching Motion – an activity

Speed

 

 

 

 

Derivative Applications – Graphing

Posted on by
Reply

Graphing and the analysis of graphs given (1) the equation, (2) a graph, or (3) a table of values of a function and its derivative(s) makes up the largest group of questions on the AP exams. Most of the other applications of the derivative depend on understanding the relationship between a function and its derivatives.

Here is a list of posts on these topics. Since this list is rather long and the topic takes more than a week to (un)cover, I will leave it as the lede post for the next two weeks.

Tangents and Slopes

Concepts Related to Graphs

The Shapes of a Graph 

Open or Closed?  Concerning intervals on which a function increases or decreases.

Extreme Values

Concavity

Joining the Pieces of a Graph

Using the Derivative to Graph the Function

Real “Real life” Graph Reading

Comparing the Graph of a Function and its Derivative  Activities on comparing the graphs using Desmos.

Writing on the AP Calculus Exams   Justifying features of the graph of a function is a major point-earner on the AP Exams.

Reading the Derivative’s Graph Summary and my most read post!

Who’d a thunk it?

Posted on by
Reply

Cubic Symmetry

Some things are fairly obvious. For example, if you look at the graphs of a few cubic equations, you might think that each is symmetric to a point and on closer inspection the point of symmetry is the point of inflection.

This is true and easy to prove. You can find the point of inflection, and then show that any point a certain distance horizontally on one side is the same distance above (or below) the point of inflection as a point the same distance horizontally on the other side is below (or above). Another way is to translate the cubic so that the point of inflection is at the origin and then show the resulting function is an odd function (i.e. symmetric to the origin).

But some other properties are not at all obvious. How someone thought to look for them is not even clear.

Tangent Line.

If you have cubic function with real roots of x = a, x = b, and x = c not necessarily distinct, if you draw a tangent line at a point where x is the average of any two roots, x = ½(a + b), , then this tangent line intersects the cubic on the x-axis at exactly the third root, x = c. Here is a Desmos graph illustrating this idea.

Here is a proof done with a CAS. The first line is a cubic expressed in terms of its roots.  The third line asks where the tangent line at x = m intersects the x-axis. The last line is the answer: x = c or whenever a = b (i.e. when the two roots are the same, in which case the tangent line is the x-axis and of course also contains x = c.

Areas
Even harder to believe is this: Draw a tangent line anywhere on a cubic. This tangent will intersect the cubic at a second point and the line and the cubic will define a region whose area is A1. From the second point draw a tangent what intersects the cubic at a third point and defines a region whose area is A2. The ratio of the areas A2/A1 = 16. I have no idea why this should be so, but it is.

Here is a proof, again by CAS: The last line marked with a square bullet is the computation of the ratio and the answer, 16, is in the lower right,

And if that’s not strange enough, inserting two vertical lines defines other regions whose areas are in the ratios shown in the figure below.

Who’d a thunk it?

.