Unit 6 develops the ideas behind integration, the Fundamental Theorem of Calculus, and Accumulation. (CED – 2019 p. 109 – 128). These topics account for about 17 – 20% of questions on the AB exam and 17 – 20% of the BC questions.
Topics 6.1 – 6.4 Working up to the FTC
Topic 6.1 Exploring Accumulations of Change Accumulation is introduced through finding the area between the graph of a function and the x-axis. Positive and negative rates of change, unit analysis.
Topic 6.2 Approximating Areas with Riemann Sums Left-, right-, midpoint Riemann sums, and Trapezoidal sums, with uniform partitions are developed. Approximating with numerical methods, including use of technology are considered. Determining if the approximation is an over- or under-approximation.
Topic 6.3 Riemann Sums, Summation Notation and the Definite Integral. The definition integral is defined as the limit of a Riemann sum.
Topic 6.4 The Fundamental Theorem of Calculus (FTC) and Accumulation Functions Functions defined by definite integrals and the FTC.
Topic 6.5 Interpreting the Behavior of Accumulation Functions Involving Area Graphical, numerical, analytical, and verbal representations.
Topic 6.6 Applying Properties of Definite Integrals Using the properties to ease evaluation, evaluating by geometry and dealing with discontinuities.
Topic 6.7 The Fundamental Theorem of Calculus and Definite Integrals Antiderivatives. (Note: I suggest writing the FTC in this form 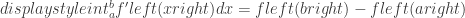 because it seem more efficient then using upper case and lower case f.)
because it seem more efficient then using upper case and lower case f.)
Topics 6.5 – 6.14 Techniques of Integration
Topic 6.8 Finding Antiderivatives and Indefinite Integrals: Basic Rules and Notation. Using basic differentiation formulas to find antiderivatives. Some functions do not have closed-form antiderivatives. (Note: While textbooks often consider antidifferentiation before any work with integration, this seems like the place to introduce them. After learning the FTC students have a reason to find antiderivatives. See Integration Itinerary
Topic 6.9 Integration Using Substitution The u-substitution method. Changing the limits of integration when substituting.
Topic 6.10 Integrating Functions Using Long Division and Completing the Square
Topic 6.11 Integrating Using Integration by Parts (BC ONLY)
Topic 6.12 Integrating Using Linear Partial Fractions (BC ONLY)
Topic 6.13 Evaluating Improper Integrals (BC ONLY) Showing the work requires students to show correct limit notation.
Topic 6.14 Selecting Techniques for Antidifferentiation This means practice, practice, practice.
Timing
The suggested time for Unit 6 is 18 – 20 classes for AB and 15 – 16 for BC of 40 – 50-minute class periods, this includes time for testing etc.
Previous posts on these topics include:
Introducing Integration
Integration Itinerary
The Old Pump and Flying to Integrationland Two introductory explorations
Working Towards Riemann Sums
Riemann Sums
The Definition of the Definite Integral
Foreshadowing the FTC
The Fundamental Theorem of Calculus
More About the FTC
Y the FTC?
Area Between Curves
Under is a Long Way Down
Properties of Integrals
Trapezoids – Ancient and Modern On Trapezoid sums
Good Question 9 – Riemann Reversed Given a Riemann sum can you find the Integral it converges to? A common and difficult AP Exam problem
Adapting 2021 AB 1 / BC 1
Adapting 2021 AB 4 / BC 4
Accumulation
Accumulation: Need an Amount?
Good Question 7 – 2009 AB 3
Good Question 8 – or Not? Unit analysis
AP Exams Accumulation Question A summary of accumulation ideas.
Graphing with Accumulation 1
Graphing with Accumulation 2
Accumulation and Differential Equations
Painting a Point
Techniques of Integrations (AB and BC)
Antidifferentiation
Why Muss with the “+C”?
Good Question 13 More than one way to skin a cat.
Integration by Parts – a BC Topic
Integration by Parts 1
Integration by Part 2
Parts and More Parts
Good Question 12 – Parts with a Constant?
Modified Tabular Integration
Improper Integrals and Proper Areas
Math vs the Real World Why  does not converge.
does not converge.
Here are links to the full list of posts discussing the ten units in the 2019 Course and Exam Description.
2019 CED – Unit 1: Limits and Continuity
2019 CED – Unit 2: Differentiation: Definition and Fundamental Properties.
2019 CED – Unit 3: Differentiation: Composite , Implicit, and Inverse Functions
2019 CED – Unit 4 Contextual Applications of the Derivative Consider teaching Unit 5 before Unit 4
2019 – CED Unit 5 Analytical Applications of Differentiation Consider teaching Unit 5 before Unit 4
2019 – CED Unit 6 Integration and Accumulation of Change
2019 – CED Unit 7 Differential Equations Consider teaching after Unit 8
2019 – CED Unit 8 Applications of Integration Consider teaching after Unit 6, before Unit 7
2019 – CED Unit 9 Parametric Equations, Polar Coordinates, and Vector-Values Functions
2019 CED Unit 10 Infinite Sequences and Series
