Matching Motion

Posted on September 16, 2015 by Lin McMullin

Here’s a little matching quiz. In the function column there is a list of properties of functions and in the motion column are a list of terms describing the motion of a particle. The two lists are very similar. Match the terms in the function list with the corresponding terms in the Linear Motion list (some may be used more than once). The answers are below. For more on this idea see my previous post Motion Problems: Same Thing, Different Context.

Function Linear Motion

1. Value of a function at x A. acceleration

2. First derivative B. “at rest”

3. Second derivative C. farthest left

4. Function is increasing D. farthest right

5. Function is decreasing E. moving to the left or down

6. Absolute Maximum F. moving to the right or up

7. Absolute Minimum G. object changes direction

8. y ʹ = 0 H. position at time t

9. y ʹ changes sign I. speed

10. Increasing & concave up J. speed is decreasing

11. Increasing & concave down K. speed is increasing

12. Decreasing & concave up L. velocity

13. Decreasing & concave down

14. Absolute value of velocity

Answers: 1. H, 2. L, 3. A, 4. F, 5. E, 6. D, 7. C, 8. B, 9. G, 10. K, 11. J, 12. J, 13. K, 14. I

Using the Derivative to Graph the Function

Posted on September 9, 2015 by Lin McMullin

In my last post I showed how to use a Desmos graph to discover, by looking at the tangent line as it moved along the graph of the function, the properties of the derivative of a function. This post goes in the opposite direction. Now, instead of discovering the properties of the derivative from the graph of the function, we will use that knowledge to identify important information about the function from the graph of its derivative. We are not discovering anything here; rather we are putting our previous discoveries to use.

One of the uses of the derivative is to deduce properties of its antiderivative, i.e. the function of which it is the derivative. This is an important skill for students to be able to use. It is also a type of question that appears on every Advanced Placement Calculus exam in both the free-response sections and the multiple-choice sections. My previous post on this topic, Reading the Derivative’s Graph, is the most read post on this blog. This post expands on the concepts in that post and shows how to use the Desmos file to help students develop the skills necessary to answer this type of question.

Desmos is free. You and your students can set up their own account and save their own work there. There are also free Desmos apps for tablets and smart phones.

Click on the graph above. Here’s what you should see:

The first equation on the left side is f(x). This is the function whose antiderivative we will be trying to create. You may change this to any function you wish.
The second equation is F(x) the antiderivative of f(x). That is F ‘(x) = f(x). Desmos cannot compute an antiderivative so you will need to enter it yourself. Your students need not trust you on this: have them check your equation by differentiating. Of course, at this point they will not be ready to find the analytic form of the antiderivative except for the simplest functions. This comes later in the year.
Note the “+C” is included and later we will manipulate this with a slider.
The antiderivative is multiplied by $\frac{\sqrt{a-x}}{\sqrt{a-x}}$ . This is a way of controlling the “a” slider and should always be multiplied by antiderivative. This is just a syntax trick to make the graph work and is not part of the antiderivative. When x is to the left of a, (x < a) the fraction is 1 and the graph will be seen; when x is to the right of a, (x > a) the expression is undefined, and nothing will graph. As you change “a” with the slider the graph of an antiderivative will be drawn.
The third equation x = a graphs a dashed vertical to help you line up the corresponding points on the two graphs.
The next two lines are the “a” and “C” sliders. Make C = 0 for now and move the “a” slider.

At this point students should know things about the relationship between a function and its first and second derivatives. This includes the things they discovered in the previous post such as when the function is increasing the derivative is non-negative, and when the tangent line is above the graph the slope (derivative) is decreasing and the graph of the function is concave down. All of these concepts are really “if, and only if” situations. So we now consider them in reverse and deduce properties of the antiderivative from the properties of the graph of the derivative.

Using the “a” slider starting at the left side of the graph ask the students what the derivative tells them about the function in this part of the domain. Is the function increasing or decreasing? Is it concave up or down? etc. Go slowly from left to right asking what happens next, and why (that is, how do you know? What feature of the derivative tells you this?) This is preparing them to write the justifications required on the AP exams.

Certain points on the graph of the derivative are important. The zeros of the derivative and whether the derivative changes from positive to negative, negative to positive, or neither are important. Likewise, the extreme values of the derivative point to important features of the function – points of inflection.

Once you have a complete graph of the antiderivative move the “C” slider.

Remind students that the derivative of a constant is zero and therefore, the C does not show up in the derivative.
Discuss is why changing the antiderivative does not change the derivative.
Ask, how many functions have the same derivative?
Point out is that by changing “C” the graph of an antiderivative can be made to go through any (every, all) point in the plane.

Switch to a different function and its derivative to reinforce the concepts. Yo will have to enter both the derivative and the antiderivative.Do this as often as necessary. You could also give students or groups of students the graph of a derivative (on paper) and challenge them to sketch the antiderivative.

A disclaimer: A function and its derivative should not be graphed on the same axes, because the two have different units. Nevertheless, I have done it here, and it is commonly done everywhere, to compare the graphs of a function and its derivative so that the important features of the two can be lined up and easily compared.

Soda Cans

Posted on May 13, 2015 by Lin McMullin

A typical calculus optimization question asks you to find the dimensions of a cylindrical soda can with a fixed volume that has a minimum surface area (and therefore is cheaper to manufacture).

Let r be the radius of the cylinder and h be its height. The volume, V, is constant and $V=\pi {{r}^{2}}h$ . The surface area including the top and bottom is given by

$S=2\pi rh+2\pi {{r}^{2}}$

Since $\displaystyle h=\frac{V}{\pi {{r}^{2}}}$ , the surface area, S, can be expressed as

$S=2V{{r}^{-1}}+2\pi {{r}^{2}}$

To find the value of r that will give the smallest surface area we find the derivative, set it equal to zero and solve for r:

$\displaystyle \frac{dS}{dr}=-2V{{r}^{-2}}+4\pi r$

This will equal zero when $\displaystyle r=\sqrt[3]{\frac{V}{2\pi }}$ and substituting into the expression above $\displaystyle h=\sqrt[3]{\frac{4V}{\pi }}$ .

Then $\displaystyle \frac{h}{r}=\sqrt[3]{\frac{\frac{4V}{\pi }}{\frac{V}{2\pi }}}=2$ , so $h=2r$ . In the optimum can the height is equal to the diameter.

The thing is that very few cans, especially beverage cans are anywhere near this “square “ shape. The closest I could find in my pantry was a tomato sauce can holding 8 oz. or 277 mL. The inside dimensions are about 65 cm. by 75cm. Compare this to the 12 oz. soda can holding 355 mL. The usual reason given for this departure from the mathematically best shape is the taller can is easier to hold especially for children.

What got me interested in this was the video below. While there is no overt calculus mentioned, there is a lot of math. There are also STEM considerations, specifically engineering. As you watch look for the math and engineering ideas that are mentioned and discuss them with your class. Here are a few:

Geometry: Why a cylinder? Why not a sphere or a cube?
Engineering: When cutting circles out of rectangular sheets of aluminum there is a lot of unused metal. Why is all this waste not a problem? This goes to materials engineering; steel is more difficult to recycle than aluminum.
Math: Efficient packing is also a consideration. Check the calculations in the video as to the most efficient way (least empty space) to pack containers. Why do they not use the most efficient?
Geometry: The (spherical) dome is a very strong shape. In what other places are domes used? Why?
Engineering: How does pressurizing the cans make them stronger?
Geometry and Engineering: The elongated ridges on the sides of non-pressurized steel cans strengthen the sides. How are these ridges similar to the dome or circular arch?
Physics: Look for a discussion of first- and second-class leavers.
Engineering: What other advantages are there to using the very thin aluminum can.

At the end of the video 6 other videos are mentioned. These are also interesting and show the same process in cartoon form and in video of the machines making cans. The links to these are here:

Rexam: http://www.youtube.com/watch?v=7dK1VV…
How It’s Made: http://www.youtube.com/watch?v=V7Y0zA…
Anim1: https://www.youtube.com/watch?v=WU_iS…
Anim2:https://www.youtube.com/watch?v=hcsDx…
Drawing: https://www.youtube.com/watch?v=DF4v-…
Redrawing: http://www.youtube.com/watch?v=iUAijp…

The Marble and the Vase

Posted on October 23, 2014 by Lin McMullin

A fairly common max/min problem asks the student to find the point on the parabola $f\left( x \right)={{x}^{2}}$ that is closest to the point $A\left( 0,1 \right)$ . The solution is not too difficult. The distance, L(x), between A and the point $\left( x,{{x}^{2}} \right)$ on the parabola is given by

$\displaystyle L\left( x \right)=\sqrt{{{\left( x-0 \right)}^{2}}+{{\left( {{x}^{2}}-1 \right)}^{2}}}=\sqrt{{{x}^{4}}-{{x}^{2}}+1}$

And the minimum distance can be found when

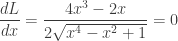
$\displaystyle \frac{dL}{dx}=\frac{4{{x}^{3}}-2x}{2\sqrt{{{x}^{4}}-{{x}^{2}}+1}}=0$

This occurs when $x=0,\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}$ . The local maximum is occurs when x = 0. The (global) minimums are the other two values located symmetrically to the y-axis.

_________________________

Somewhere I saw this problem posed in terms of a marble dropped into a vase shaped like a parabola. So I think of it that way. This accounts for the title of the post. The problem is, however, basically a two-dimensional situation.

In this post I would like to expand and explore this problem. The exploration will, I hope, give students some insight and experience with extreme values, and the relationship between a graph and its derivative. I will pose a series of questions that you could give to your students to explore. I will answer the questions as I go, but you, of course, should not do that until your students have had some time to work on the questions.

Graphing technology and later Computer Algebra Systems (CAS) will come in handy.

_________________________

1. Consider a general point $A\left( 0,a \right)$ on the y-axis. Find the x-coordinates of the closest point on the parabola in terms of a.

The distance is now given by

$\displaystyle L\left( x \right)=\sqrt{{{\left( x-0 \right)}^{2}}+{{\left( {{x}^{2}}-a \right)}^{2}}}=\sqrt{{{x}^{4}}+\left( 1-2a \right){{x}^{2}}+{{a}^{2}}}$

$\displaystyle \frac{dL}{dx}=\frac{2{{x}^{3}}+\left( 1-2a \right)x}{\sqrt{{{x}^{4}}+2\left( 1-2a \right){{x}^{2}}+{{a}^{2}}}}$

And $\frac{dL}{dx}=0$ when $x=0,\frac{\sqrt{2\left( 2a-1 \right)}}{2},-\frac{\sqrt{2\left( 2a-1 \right)}}{2}$

The (local) maximum is at x = 0. The other values are the minimums. The CAS computation is shown at the end of the post. This is easy enough to do by hand.

2. Discuss the equation ${{L}^{2}}={{x}^{2}}+{{\left( x-a \right)}^{2}}$ in relation to this situation.

This is the equation of a circle with center at A with radius of L. At the minimum distance this circle will be tangent to the parabola.

3. What happens when $a=\tfrac{1}{2}$ and when $a<\tfrac{1}{2}$ ?

When $a=\tfrac{1}{2}$ , the three zeroes are the same. The circle is tangent to the parabola at the origin and a is the minimum distance.

When $a<\tfrac{1}{2}$ , the circle does not intersect the parabola. Notice that in this case two of the roots of $\frac{dL}{dt}=0$ are not Real numbers.

4. Consider the distance, L(x), from point A to the parabola. As x moves from left to right describe how this length changes. Be specific. Sketch the graph of this distance y = L(x). Where are its (local) maximum and minimum values, relative to the parabola and the circle tangent to the parabola?

The clip below illustrates the situation. The two segments marked L(x) are congruent. The graph of y = L(x) is a“w” shape similar to but not quartic polynomial. The minimums occur directly under the points of tangency of the circle and the parabola. The local maximum is directly over the origin. Is it coincidence that the graph goes through the center of the circle? Explain.

5. Graph $y=\frac{dL}{dx}$ and compare its graph with the graph of $y=L(x)$

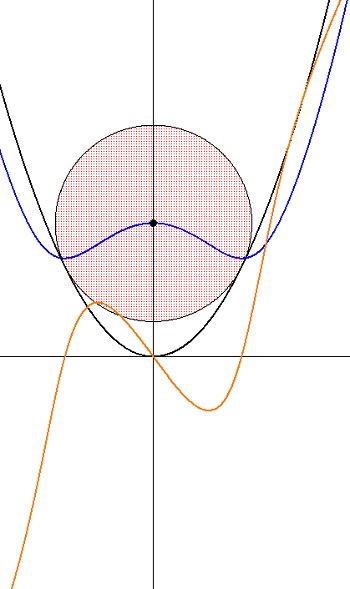
L(x) is the blue graph and and L'(x) is the orange graph.
Notice the concavity of L'(x)

6. The graph of $y=\frac{dL}{dx}$ appears be concave up, then down, then (after passing the origin) up, and then down again. There are three points of inflection. Find their x-coordinates in terms of a. How do these points relate to y = L(x) ? (Use a CAS to do the computation)

The points of inflection of the derivative can be found from the second derivative of the derivative (the third derivative of the L(x)). The abscissas are $x=-\sqrt{a},x=0,\text{ and }\sqrt{a}$ . The CAS computation is shown below

CAS Computation for questions 1 and 6.

Mean Numbers

Posted on September 25, 2013 by Lin McMullin

Here is a problem for you and your students. The numbers are mean until you get to the end when they all become very nice and well-behaved.

You could give this to your students individually or as a group exploration. Give each person or group a different function and/or different intervals. Choose a function that has several (3 – 5) turning points in the interval. The function should be differentiable on the open interval and continuous on the closed interval.

It is intended that the work be done on a graphing calculator; you will need to carry 6 or 7 decimal places in their work.

Here is a typical problem. A link to the solution is given at the end.

Consider the function $f\left( x \right)=\sin \left( x \right)$ on the closed interval [1, 12].

Write an equation of a line, $y\left( x \right)$ , between the endpoints of the function. Give the decimal value of its slope and give a graph of the function and the line.
Write the equation of a function $h\left( x \right)$ that gives the vertical distance between $f\left( x \right)$ and $y\left( x \right)$ . Since f may be both above and below y this function may have positive and negative values.
Graph h and find its critical values. What are these places with respect to the graph of h?
Calculate the derivative of f at the critical values of h.
Interpret your result graphically.

Click here for the solution.

More Gold

Posted on July 17, 2013 by Lin McMullin

Last week I discussed Lin McMullin’s Theorem (that would be me). The theorem finds where the Golden Ratio shows up in any fourth-degree polynomial. Shortly after that began making the rounds, I got an e-mail from David Tschappat who was then a senior in college. He is now a doctoral student working for an online learning solutions provider.

He related the discovery of a similar appearance of the Golden Ratio in cubic polynomials! Here is his theorem and two other related facts about cubic polynomials (lemmas really) as developed by me.

All cubic polynomials are symmetric to their point of inflection. Therefore, we can simplify matters by translating any cubic so that its point of inflection is at the origin. The general equation will then be $f\left( x \right)=k{{x}^{3}}-3{{h}^{2}}kx$ .

I choose this rather unusual form so that the x-coordinates of the extreme points will be “nice” variables, namely h and –h the zeros of ${f}'\left( x \right)=3k{{x}^{2}}-3{{h}^{2}}k=3k\left( x-h)(x+h \right)$ . The leading coefficient k will eventually divide out and not be a concern.

Now consider two other values x = –2h and x = 2h. So, assuming h > 0, there are five evenly spaced values $-2h<-h<0<h<2h$ that we will consider.

The first two results I will leave as an exercise, as they say:

$f\left( -2h \right)=f\left( h \right)$ and $f\left( -h \right)=f\left( 2h \right)$ . This means that the extreme values are the same as a point on the graph 3h units away on the other side of the y-axis. This is mildly interesting in itself. The reason it is mentioned id that we will use these points soon.
${f}'\left( -2h \right)={f}'\left( 2h \right)$ which is really true for any points at equal distances on opposite sides of the origin. This is obvious from the symmetry of the cubic.

Now comes the interesting and strange part. An equation of a line through one extreme point with a slope equal to that at the point with the same y-coordinate on the other side of the origin (or for that matter the point h units farther away on the same side of the y-axis) is

$y=f\left( -h \right)+{f}'\left( 2h \right)\left( x-\left( -h \right) \right)$

$y=\left( k{{\left( -h \right)}^{3}}-3{{h}^{2}}k\left( -h \right) \right)+\left( 3k{{\left( 2h \right)}^{2}}-3{{h}^{2}}k \right)\left( x+h \right)$

$y=k\left( 11{{h}^{3}}+9{{h}^{2}}x \right)$

Now find where this line intersect the original cubic by solving $y=f\left( x \right)$ . The equation can be solved by hand. We know that x = h is one solution. Synthetic division will give a quadratic and the quadratic formula will do the rest.

$k\left( 11{{h}^{3}}+9{{h}^{2}}x \right)=k{{x}^{3}}-3{{h}^{2}}kx$

$0={{x}^{3}}-12{{h}^{2}}x-11{{h}^{3}}$

$0=\left( x-h \right)\left( {{x}^{2}}+hx-11{{h}^{2}} \right)$

$\displaystyle x=h,\frac{1+3\sqrt{5}}{2}h,\frac{1-3\sqrt{5}}{2}h$

What? You were expecting the Golden Ratio? Not to worry; it’s there!

$\displaystyle \Phi \left( -h \right)+\phi \left( 2h \right)=\frac{1+\sqrt{5}}{2}\left( -h \right)+\frac{1-\sqrt{5}}{2}\left( 2h \right)=\frac{1-3\sqrt{5}}{2}h$

$\displaystyle \Phi \left( 2h \right)+\phi \left( -h \right)=\frac{1+\sqrt{5}}{2}\left( 2h \right)+\frac{1-\sqrt{5}}{2}\left( -h \right)=\frac{1+3\sqrt{5}}{2}h$

Where $\displaystyle \Phi =\frac{1+\sqrt{5}}{2}$ is the Golden Ratio and $\displaystyle \phi ={{\Phi }^{-1}}=\frac{1-\sqrt{5}}{2}$ is the reciprocal of the Golden Ratio.

A similar computation using the other extreme point gives similar results.

Yes, the Golden Ratio is there; I don’t know why it should be there, but it is.

Thank you, David.

Variations on a Theme by ETS

Posted on June 14, 2013 by Lin McMullin

Experienced AP calculus teacher use as many released exam questions during the year as they can. They are good questions and using them gets the students used to the AP style and format. They can be used “as is”, but many are so rich that they can be tweaked to test other concepts and to make the students think wider and deeper.

Below is a multiple-choice question from the 2008 AB calculus exam, question 9.

The graph of the piecewise linear function f is shown in the figure above. If $\displaystyle g\left( x \right)=\int_{-2}^{x}{f\left( t \right)\,dt}$ , which of the following values is the greatest?

(A) g(-3) (B) g(-2) (C) g(0) (D) g(1) (E) g(2)

I am now going to suggest some ways to tweak this question to bring out other ideas. Here are my suggestions. Some could be multiple-choice others simple short constructed response questions. A few of these questions, such as 3 and 4, ask the same thing in different ways.

1. 1. Require students to show work or justify their answer even on multiple-choice questions. So for this question they should write, “The answer is (D) g(1) since x = 1 is the only place where ${g}'\left( x \right)=f\left( x \right)$ changes from positive to negative.”
  2. Ask, “Which of the following values is the least?” (Same choices)
  3. Find the five values listed.
  4. Put the five values in order from smallest to largest.
  5. If $\displaystyle g\left( x \right)=g\left( -2 \right)+\int_{-2}^{x}{f\left( t \right)dt}$ and the maximum value of g is 7, what is the minimum value?
  6. If $\displaystyle g\left( x \right)=g\left( -2 \right)+\int_{-2}^{x}{f\left( t \right)dt}$ and the minimum value of g is 7, what is the maximum value?
  7. Pick any number (not just an integers) in the interval [–3, 2] to be a and change the stem to read, “If $\displaystyle g\left( x \right)=g\left( a \right)+\int_{a}^{x}{f\left( t \right)dt}$ ….” And then ask any of the questions above – some answers will be different, some will be the same. Discussing which will not change and why makes a worthwhile discussion.
  8. Change the equation in the stem to $\displaystyle g\left( x \right)=3x+\int_{-2}^{x}{f\left( t \right)dt}$ and ask the questions above. Again most of the answers will change. Also this question and the next start looking like some free-response questions. Compare them with 2011 AB 4 and 2010 AB 5(c)
  9. Change the equation in the stem to $\displaystyle g\left( x \right)=-\tfrac{3}{2}x+\int_{-2}^{x}{f\left( t \right)dt}$ and ask the questions above. This time most of the answers will change.
  10. Change the graph and ask the same questions.