Curves with Extrema?

Posted on October 19, 2015 by Lin McMullin

We spend a lot of time in calculus studying curves. We look for maximums, minimums, asymptotes, end behavior, and on and on, but what about in “real life”?

For some time, I’ve been trying to find a real situation determined or modeled by a non-trigonometric curve with more than one extreme value. I’ve not been very successful. I knew of only one and discovered a second in writing this post. Here is an example that illustrates what I mean.

Example 1: This is a very common calculus example. Squares are cut from the corners of a cardboard sheet that measures 20 inches by 40 inches. The remaining sides are folded up to make a box. How large should the squares be to make a box of the largest possible volume?

If we let x = the length of the side of the square, then the volume of the box is given by V = x (20 –2 x)(40 – 2x)

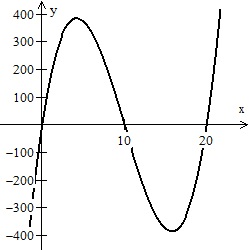
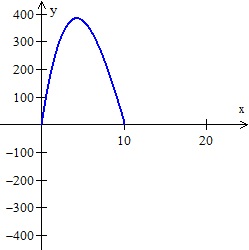
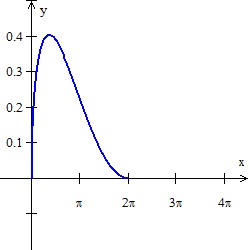
The graph of the volume is shown in Figure 1 and sure enough we have a polynomial curve that has two extreme values. But wait. Do we really have two extreme values? The domain of the equation appears to be all real numbers, but in fact it is 0 < x < 10, since x cannot be negative, and if x > 10, then the (20 –2 x) side is negative and that won’t work either. Figure 2 shows the true situation. There is only one extreme value.

: Figure 1

: Figure 2

Example 2: This is also an optimization problem, but a bit more difficult. A sector is cut from a circular paper disk of radius 1. The remaining part of the disk is formed into a cone. How long should the curved part of the sector be so that the cone has the maximum volume? You might want to try this before you read further.

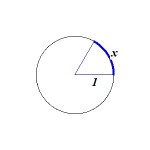
Let x be the length of curved part of the sector See Figure 3.

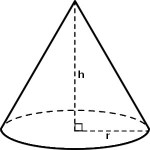
The radius of the disk becomes the slant height of the cone. The circumference of the disk is $2\pi \left( 1 \right)$ and so the circumference of the base of the cone is $C=2\pi \left( 1 \right)-x$ and its radius is $\displaystyle r=\frac{2\pi -x}{2\pi }=1-\frac{x}{2\pi }$ . The height, h of the cone is $\displaystyle h=\sqrt{1-{{\left( \frac{x}{2\pi } \right)}^{2}}}$ . See figure 4.

: Figure 3

: Figure 4

The volume of the cone is . $\displaystyle V=\frac{\pi }{3}{{\left( 1-\frac{x}{2\pi } \right)}^{2}}\sqrt{{{1}^{2}}-{{\left( 1-\frac{x}{2\pi } \right)}^{2}}}$

The graph of this equation is shown in Figure 5, and has two maximum values and a minimum. The domain appears to be $0<x<4\pi$ . But if $x>2\pi$ the piece you cut out will be larger than the original disk (and the expression under the radical will be negative). So our domain will be $0<x<2\pi$ (the endpoints correspond to not cutting any sector or cutting away the entire disk. The graph is shown in Figure 6 with, alas, only one extreme value.

: Figure 5

: Figure 6

(For the original expression the minimums are at $x=0,\ 2\pi ,\text{ and }4\pi$ and the maximums are at $x\approx 1.153\text{ and }x\approx 11.413$ . A CAS will help with these calculations or just use a graphing calculator.)

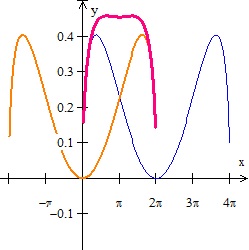
Extension 1: Find the value of x that will make the largest volume when the piece cut out is formed into a cone. Compare the two graphs and explain their congruence. See Figure 7.
Extension 2: Here I finally found what I was after. – a situation with more than one extreme value. Find the value of x that will make the largest total volume formed when the volume of the original cone and the cone formed by the piece cut out. Compare the first two graphs and the graph of this volume. See figure 8 – the magenta graph.

: Figure 7

: Figure 8

The Mae West Curve

There is at least one real situation that is modeled by a function with several extreme values. Spud’s blog gives the following explanation and illustration.

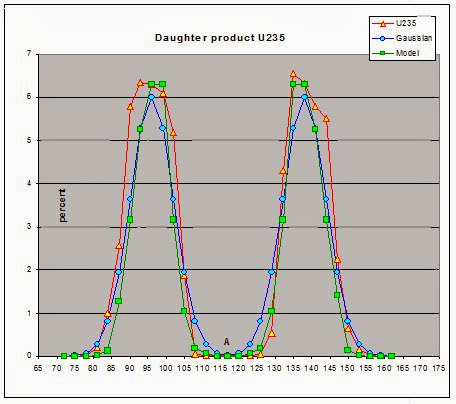
“When a Uranium (or Plutonium) atom fission, or splits, you end up with two much lighter atoms, called fission products, or daughter nuclides. The U-235 nucleus can split into a myriad of combinations, but some combinations are more likely than others.

“[Figure 9 below] shows the percentage of fission products by [atomic] mass[, A]. [This is] called the Mae West curve. … Note that the more likely fission products have two peaks at a mass of about 95 and 135.”

Thus we have a real life illustration of a model that has three extreme values in its domain.

The model graphed in Figure 9 is known as the “Mae West Curve,” named after Mae West (1893 – 1980) and actress, playwright and screenwriter.

: Figure 9: The “Mae West” Curve

If you know of any other real situations with more than one extreme, please let us know. Use the “comment” button below.

Soda Cans

Posted on May 13, 2015 by Lin McMullin

A typical calculus optimization question asks you to find the dimensions of a cylindrical soda can with a fixed volume that has a minimum surface area (and therefore is cheaper to manufacture).

Let r be the radius of the cylinder and h be its height. The volume, V, is constant and $V=\pi {{r}^{2}}h$ . The surface area including the top and bottom is given by

$S=2\pi rh+2\pi {{r}^{2}}$

Since $\displaystyle h=\frac{V}{\pi {{r}^{2}}}$ , the surface area, S, can be expressed as

$S=2V{{r}^{-1}}+2\pi {{r}^{2}}$

To find the value of r that will give the smallest surface area we find the derivative, set it equal to zero and solve for r:

$\displaystyle \frac{dS}{dr}=-2V{{r}^{-2}}+4\pi r$

This will equal zero when $\displaystyle r=\sqrt[3]{\frac{V}{2\pi }}$ and substituting into the expression above $\displaystyle h=\sqrt[3]{\frac{4V}{\pi }}$ .

Then $\displaystyle \frac{h}{r}=\sqrt[3]{\frac{\frac{4V}{\pi }}{\frac{V}{2\pi }}}=2$ , so $h=2r$ . In the optimum can the height is equal to the diameter.

The thing is that very few cans, especially beverage cans are anywhere near this “square “ shape. The closest I could find in my pantry was a tomato sauce can holding 8 oz. or 277 mL. The inside dimensions are about 65 cm. by 75cm. Compare this to the 12 oz. soda can holding 355 mL. The usual reason given for this departure from the mathematically best shape is the taller can is easier to hold especially for children.

What got me interested in this was the video below. While there is no overt calculus mentioned, there is a lot of math. There are also STEM considerations, specifically engineering. As you watch look for the math and engineering ideas that are mentioned and discuss them with your class. Here are a few:

Geometry: Why a cylinder? Why not a sphere or a cube?
Engineering: When cutting circles out of rectangular sheets of aluminum there is a lot of unused metal. Why is all this waste not a problem? This goes to materials engineering; steel is more difficult to recycle than aluminum.
Math: Efficient packing is also a consideration. Check the calculations in the video as to the most efficient way (least empty space) to pack containers. Why do they not use the most efficient?
Geometry: The (spherical) dome is a very strong shape. In what other places are domes used? Why?
Engineering: How does pressurizing the cans make them stronger?
Geometry and Engineering: The elongated ridges on the sides of non-pressurized steel cans strengthen the sides. How are these ridges similar to the dome or circular arch?
Physics: Look for a discussion of first- and second-class leavers.
Engineering: What other advantages are there to using the very thin aluminum can.

At the end of the video 6 other videos are mentioned. These are also interesting and show the same process in cartoon form and in video of the machines making cans. The links to these are here:

Rexam: http://www.youtube.com/watch?v=7dK1VV…
How It’s Made: http://www.youtube.com/watch?v=V7Y0zA…
Anim1: https://www.youtube.com/watch?v=WU_iS…
Anim2:https://www.youtube.com/watch?v=hcsDx…
Drawing: https://www.youtube.com/watch?v=DF4v-…
Redrawing: http://www.youtube.com/watch?v=iUAijp…

The Marble and the Vase

Posted on October 23, 2014 by Lin McMullin

A fairly common max/min problem asks the student to find the point on the parabola $f\left( x \right)={{x}^{2}}$ that is closest to the point $A\left( 0,1 \right)$ . The solution is not too difficult. The distance, L(x), between A and the point $\left( x,{{x}^{2}} \right)$ on the parabola is given by

$\displaystyle L\left( x \right)=\sqrt{{{\left( x-0 \right)}^{2}}+{{\left( {{x}^{2}}-1 \right)}^{2}}}=\sqrt{{{x}^{4}}-{{x}^{2}}+1}$

And the minimum distance can be found when

$\displaystyle \frac{dL}{dx}=\frac{4{{x}^{3}}-2x}{2\sqrt{{{x}^{4}}-{{x}^{2}}+1}}=0$

This occurs when $x=0,\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}$ . The local maximum is occurs when x = 0. The (global) minimums are the other two values located symmetrically to the y-axis.

_________________________

Somewhere I saw this problem posed in terms of a marble dropped into a vase shaped like a parabola. So I think of it that way. This accounts for the title of the post. The problem is, however, basically a two-dimensional situation.

In this post I would like to expand and explore this problem. The exploration will, I hope, give students some insight and experience with extreme values, and the relationship between a graph and its derivative. I will pose a series of questions that you could give to your students to explore. I will answer the questions as I go, but you, of course, should not do that until your students have had some time to work on the questions.

Graphing technology and later Computer Algebra Systems (CAS) will come in handy.

_________________________

1. Consider a general point $A\left( 0,a \right)$ on the y-axis. Find the x-coordinates of the closest point on the parabola in terms of a.

The distance is now given by

$\displaystyle L\left( x \right)=\sqrt{{{\left( x-0 \right)}^{2}}+{{\left( {{x}^{2}}-a \right)}^{2}}}=\sqrt{{{x}^{4}}+\left( 1-2a \right){{x}^{2}}+{{a}^{2}}}$

$\displaystyle \frac{dL}{dx}=\frac{2{{x}^{3}}+\left( 1-2a \right)x}{\sqrt{{{x}^{4}}+2\left( 1-2a \right){{x}^{2}}+{{a}^{2}}}}$

And $\frac{dL}{dx}=0$ when $x=0,\frac{\sqrt{2\left( 2a-1 \right)}}{2},-\frac{\sqrt{2\left( 2a-1 \right)}}{2}$

The (local) maximum is at x = 0. The other values are the minimums. The CAS computation is shown at the end of the post. This is easy enough to do by hand.

2. Discuss the equation ${{L}^{2}}={{x}^{2}}+{{\left( x-a \right)}^{2}}$ in relation to this situation.

This is the equation of a circle with center at A with radius of L. At the minimum distance this circle will be tangent to the parabola.

3. What happens when $a=\tfrac{1}{2}$ and when $a<\tfrac{1}{2}$ ?

When $a=\tfrac{1}{2}$ , the three zeroes are the same. The circle is tangent to the parabola at the origin and a is the minimum distance.

When $a<\tfrac{1}{2}$ , the circle does not intersect the parabola. Notice that in this case two of the roots of $\frac{dL}{dt}=0$ are not Real numbers.

4. Consider the distance, L(x), from point A to the parabola. As x moves from left to right describe how this length changes. Be specific. Sketch the graph of this distance y = L(x). Where are its (local) maximum and minimum values, relative to the parabola and the circle tangent to the parabola?

The clip below illustrates the situation. The two segments marked L(x) are congruent. The graph of y = L(x) is a“w” shape similar to but not quartic polynomial. The minimums occur directly under the points of tangency of the circle and the parabola. The local maximum is directly over the origin. Is it coincidence that the graph goes through the center of the circle? Explain.

5. Graph $y=\frac{dL}{dx}$ and compare its graph with the graph of $y=L(x)$

L(x) is the blue graph and and L'(x) is the orange graph.
Notice the concavity of L'(x)

6. The graph of $y=\frac{dL}{dx}$ appears be concave up, then down, then (after passing the origin) up, and then down again. There are three points of inflection. Find their x-coordinates in terms of a. How do these points relate to y = L(x) ? (Use a CAS to do the computation)

The points of inflection of the derivative can be found from the second derivative of the derivative (the third derivative of the L(x)). The abscissas are $x=-\sqrt{a},x=0,\text{ and }\sqrt{a}$ . The CAS computation is shown below

CAS Computation for questions 1 and 6.

Why Radians?

Posted on October 12, 2012 by Lin McMullin

Calculus is always done in radian measure. Degree (a right angle is 90 degrees) and gradian measure (a right angle is 100 grads) have their uses. Outside of the calculus they may be easier to use than radians. However, they are somewhat arbitrary. Why 90 or 100 for a right angle? Why not 10 or 217?

Radians make it possible to relate a linear measure and an angle measure. A unit circle is a circle whose radius is one unit. The one-unit radius is the same as one unit along the circumference. Wrap a number line counterclockwise around a unit circle starting with zero at (1, 0). The length of the arc subtended by the central angle becomes the radian measure of the angle.

This keeps all the important numbers like the sine and cosine of the central angle, on the same scale. When you graph y = sin(x) one unit in the x-direction is the same as one unit in the y-direction. When graphing using degrees, the vertical scale must be stretched a lot to even see that the graph goes up and down. Try graphing on a calculator y = sin(x) in degree mode in a square window and you will see what I mean.

But the utility of radian measure is even more obvious in calculus. To develop the derivative of the sine function you first work with this inequality (At the request of a reader I have added an explanation of this inequality at the end of the post):

$\displaystyle \frac{1}{2}\cos \left( \theta \right)\sin \left( \theta \right)\le \frac{1}{2}\theta \le \frac{1}{2}\tan \left( \theta \right)$

From this inequality you determine that $\displaystyle \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \left( \theta \right)}{\theta }=1$

The middle term of the inequality is the area of a sector of a unit circle with central angles of $\theta$ radians. If you work in degrees, this sector’s area is $\displaystyle \frac{\pi }{360}\theta$ and you will find that $\displaystyle \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \left( \theta \right)}{\theta }=\frac{\pi }{180}$ .

This limit is used to find the derivative of the sin(x). Thus, with x in degrees, $\displaystyle \frac{d}{dx}\sin \left( x \right)=\frac{\pi }{180}\cos \left( x \right)$ . This means that with the derivative or antiderivative of any trigonometric function that $\displaystyle \frac{\pi }{180}$ is there getting in the way.

Who needs that?

Do your calculus in radians.

Revision December 7, 2014: The inequality above is derived this way. Consider the unit circle shown below.

1. The central angle is $\theta$ and the coordinates of A are $\left( \cos (\theta ),\sin (\theta ) \right)$ .

Then the area of triangle OAB is $\frac{1}{2}\cos \left( \theta\right)\sin \left( \theta\right)$

2. The area of sector $OAD=\frac{\theta}{2\pi }\pi {{\left( 1 \right)}^{2}}=\frac{1}{2}\theta$ . The sector’s area is larger than the area of triangle OAB.

3. By similar triangles $\displaystyle \frac{AB}{OB}=\frac{\sin \left( \theta\right)}{\cos \left( \theta\right)}=\tan \left( \theta\right)=\frac{CD}{1}=CD$ .

Then the area of $\Delta OCD=\frac{1}{2}CD\cdot OD=\frac{1}{2}\tan \left( \theta \right)$ This is larger than the area of the sector, which establishes the inequality above.

Multiply the inequality by $\displaystyle \frac{2}{\sin \left( \theta \right)}$ and take the reciprocal to obtain $\displaystyle \frac{1}{\cos \left( \theta \right)}\ge \frac{\sin \left( \theta \right)}{\theta }\ge \cos \left( \theta \right)$ .

Finally, take the limit of these expression as $\theta \to 0$ and the limit $\displaystyle \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \left( \theta \right)}{\theta }=1$ is established by the squeeze theorem.