Why Radians?

Lin McMullin / October 12, 2012

Calculus is always done in radian measure. Degree (a right angle is 90 degrees) and gradian measure (a right angle is 100 grads) have their uses. Outside of the calculus they may be easier to use than radians. However, they are somewhat arbitrary. Why 90 or 100 for a right angles? Why not 10 or 217?

Radians make it possible to relate a linear measure and an angle measure. A unit circle is a circle whose radius is one unit. The one unit radius is the same as one unit along the circumference. Wrap a number line counterclockwise around a unit circle starting with zero at (1, 0). The length of the arc subtended by the central angle becomes the radian measure of the angle.

This keeps all the important numbers like the sine and cosine of the central angle, on the same scale. When you graph y = sin(x) one unit in the x-direction is the same as one unit in the y-direction. When graphing using degrees, the vertical scale must be stretched a lot to even see that the graph goes up and down. Try graphing on a calculator y = sin(x) in degree mode in a square window and you will see what I mean.

But the utility of radian measure is even more obvious in calculus. To develop the derivative of the sine function you first work with this inequality (At the request of a reader I have added an explanation of this inequality at the end of the post):

$\displaystyle \frac{1}{2}\cos \left( \theta \right)\sin \left( \theta \right)\le \frac{1}{2}\theta \le \frac{1}{2}\tan \left( \theta \right)$

From this inequality you determine that $\displaystyle \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \left( \theta \right)}{\theta }=1$

The middle term of the inequality is the area of a sector of a unit circle with central angles of $\theta$ radians. If you work in degrees, this sector’s area is $\displaystyle \frac{\pi }{360}\theta$ and you will find that $\displaystyle \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \left( \theta \right)}{\theta }=\frac{\pi }{180}$ .

This limit is used to find the derivative of the sin(x). Thus, with x in degrees, $\displaystyle \frac{d}{dx}\sin \left( x \right)=\frac{\pi }{180}\cos \left( x \right)$ . This means that with the derivative or antiderivative of any trigonometric function that $\displaystyle \frac{\pi }{180}$ is there getting in the way.

Who needs that?

Do your calculus in radians.

Revision December 7, 2014: The inequality above is derived this way. Consider the unit circle shown below.

1. The central angle is $\theta$ and the coordinates of A are $\left( \cos (\theta ),\sin (\theta ) \right)$ .

Then the area of triangle OAB is $\frac{1}{2}\cos \left( \theta\right)\sin \left( \theta\right)$

2. The area of sector $OAD=\frac{\theta}{2\pi }\pi {{\left( 1 \right)}^{2}}=\frac{1}{2}\theta$ . The sector’s area is larger than the area of triangle OAB.

3. By similar triangles $\displaystyle \frac{AB}{OB}=\frac{\sin \left( \theta\right)}{\cos \left( \theta\right)}=\tan \left( \theta\right)=\frac{CD}{1}=CD$ .

Then the area of $\Delta OCD=\frac{1}{2}CD\cdot OD=\frac{1}{2}\tan \left( \theta \right)$ This is larger than the area of the sector, which establishes the inequality above.

Multiply the inequality by $\displaystyle \frac{2}{\sin \left( \theta \right)}$ and take the reciprocal to obtain $\displaystyle \frac{1}{\cos \left( \theta \right)}\ge \frac{\sin \left( \theta \right)}{\theta }\ge \cos \left( \theta \right)$ .

Finally, take the limit of these expression as $\theta \to 0$ and the limit $\displaystyle \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \left( \theta \right)}{\theta }=1$ is established by the squeeze theorem.

24 thoughts on “Why Radians?”

Baron says:

August 14, 2021 at 01:48

Hello Lin,

Thank you so much for this article. I’ve been searching and searching over the internet to understand a concept for my Surveying Class. Yet, even with your amazing description, I’m still finding it hard to understand an equation. I was wondering if you’re able to help?

In Surveying, we use the Whole Circle Bearing (WCB) or Polar Coordinates, for all of our traverse calculations and convert that to rectangular coordinates to get the precise location of a point. Our lecturer gave us an assignment to create an excel traverse calculation sheet, which I’ve successfully completed. However, he then went on to say, explain how the equation: distance*COS(Radians(WCB angle)) & distance*SIN(Radians(WCB angle)), works to give us the rectangular coordinates.

I have researched the unit circle and and how COS and SIN form a relationship with Radians in that unit circle, as you have described, in your own words above: “Radians make it possible to relate a linear measure and an angle measure”, which really helped me relate the two to a sense. But, I seem to keep falling short of the exact way in which the two work together to create the rectangular coordinate.

What I think I’ve understood so far is that, the equation is effectively: distance*COS((π/180°)*WCB angle). I’ll leave out the “WCB” portion, from here on, to make it tidier. By working through the formula, using the BODMAS method, and completing π/180°*angle first (Radians setting on in calculator), it gives us the Radian conversion of the angle.

Using the following sample numbers:
Distance: 63.25m & Angle: 85°, the equation is: 63.25*COS((π/180°)*85°)
Therefore, (π/180°)*85° = 1.483529864 Radians, (180°/π = 57.29577951°)
=> (change calculator to degrees) 63.25*(COS(57.29577951°*1.483529864 Rad)) = 5.512mN = x coordinate (rounding to 3 decimal places using the even rounding system)
Repeat the above using SIN to get the y coordinate: 63.009mE (rounding to 3 decimal places using the even rounding system)

Taking just the portion of the equations:
(COS(57.29577951°*1.483529864 Rad)) or COS(84.99999998°) = 0.08715574302 radians or 4.993656235° and,
(SIN(57.29577951°*1.483529864 Rad)) or SIN(84.99999998°) = 0.9961946981 radians or 57.07775177°,
before multiplying it by the distance, it is here that I’ve reached an impass of understanding where these values fit. I.E. – I’ve drawn the above in AutoCAD yet, I’m unable to place the triangles, of the Pythagoras Theorum (SOH & CAH), when COS is multiplied with 84.99999998° and yet SIN is as well.

I feel like I’m missing something really simple.

Your help would be much appreciated

LikeLike

Reply
- Lin McMullin says:
  
  August 16, 2021 at 11:40
  
  Hi Baron. Thanks for writing.
  
  In Polar Coordinates a point is designated by the pair (r, θ) where r = the distance from the origin (a/k/a the pole) and θ is the angle measured counterclockwise from the positive part of the x-axis (a/k/a the polar axis).
  
  Consider a point in the first quadrant (r, θ). Drop a perpendicular from the point to the x-axis. This forms a right triangle with hypotenuse of r. By right triangle trigonometry the length of this segment is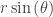 $r\sin \left( \theta \right)$ and the distance from the pole to the foot of the perpendicular is . $r\cos \left( \theta \right)$ . So the x-y-coordinates of (r, θ) are
  
  $x=r\cos \left( \theta \right)$
  $y=r\sin \left( \theta \right)$
  
  These same equations work for points in other quadrants and for angles with a negative measure (i.e., measured clockwise), because the signs of the sine and cosine for angles outside the first quadrant will take care of that.
  
  To change from an angle measure in degrees to the same angle measured in radians multiply the degrees by π/180.
  
  Calculations may be done in degrees or radians as long as the calculator or computer you are using is set in the proper mode. If your calculator or computer is set for degrees, there is no need to convert to radians. If your angles are measured in degrees, use degree mode on your device.
  
  If your distance is 63.25 meters and your angle is 85 degrees, then here is how to do the calculations. Your examples are correct, but unduly long. There is no need to do things step by step; any calculator or computer or spreadsheet will do the work for you. That is, there is no need to change back and forth between degrees and radians.
  
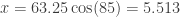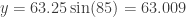  With your calculator in degree mode: $x=63.25\cos (85)=5.513$ and $y=63.25\sin (85)=63.009$ .
  
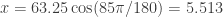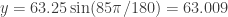  With your calculator in radian mode enter $x=63.25\cos (85\pi /180)=5.513$ and $y=63.25\sin (85\pi /180)=63.009$ .
  
  Either way, the point in polar form (63.25, 85 degrees) is (5.513, 63.009) in rectangular form.
  I hope this answers your questions. If not, write again.
  
  BTW I worked for my four years in college for a land surveyor. Work I very much enjoyed. Of course, back then we used optical transits (theodolites) reading the angles with a vernier scale and measured distance with a steel tape.
  
  LikeLike
  
  Reply
- Baron says:
  
  August 31, 2021 at 19:33
  
  Hello Lin,
  Thank you so very much for your fantastic reply. I’ve been trying to respond for a while now but was having issues getting WordPress to accept my login.
  
  The equation that our tutor gave us: distance x cos(radians(angle)) did make me wonder why we were going back and forth as you stated below “Your examples are correct, but unduly long. There is no need to do things step by step; any calculator or computer or spreadsheet will do the work for you. That is, there is no need to change back and forth between degrees and radians.”
  
  I don’t know why he asked us to use that formula. In the beginning I thought it was due to excel needing the formula that way in order to work, but I think that’s not true.
  
  “BTW I worked for my four years in college for a land surveyor. Work I very much enjoyed. Of course, back then we used optical transits (theodolites) reading the angles with a vernier scale and measured distance with a steel tape.”
  That is so cool. Before we were progressed to the new theodolites (Total Stations with laser) we had to do a levelling run using the old dumpy or automatic level and a staff/stave. That was quite fun to do.
  
  Thanks again for your reply and help. Very much appreciated.
  
  Baron
  
  LikeLike
  
  Reply
  - Lin McMullin says:
    
    September 1, 2021 at 13:34
    
    Baron
    Apparently Excel is set to work in radians. To use degrees you do have to use the formulas your teachers gave you: sin (pi( )/180) etc. I cannot find a setting that changes the default input to degrees, which, if it’s really not there, I think is kind of strange, since engineers and surveyors etc. work in degrees and use Excel.
    Leveling rods: I remember them. Real 16.5 foot rods just like they told us in high school. 4 rods = 1 chain (66 feet). Ten square chains = 1 acre = 43,560 square feet. Of course by then our steel chains were 100 feet, marked in decimal feet, not inches – some improvement. You can buy real 66 foot chains on Ebay!
    
    LikeLike
Mina says:

February 8, 2020 at 18:39

I disagree with having the inequality with equal sign. It must be 1/2 * cos(x) * sin(x) < 1/2 * x < 1/2 * tan(x) not 1/2 * cos(x) * sin(x) <= 1/2 * x <= 1/2 * tan(x)

LikeLike

Reply
- Lin McMullin says:
  
  February 11, 2020 at 10:44
  
  When you later apply the squeeze theorem and the two outside expressions become 1, you need the = sign to conclude that the middle expression also goes to 1. Also, the inequalities muust hold when x = 0, when all three parts become zero and are equal.
  
  LikeLike
  
  Reply
Pingback: Trigonometric Recipes for SwiftUI - The SwiftUI Lab
Brian Vincent Walker says:

September 18, 2018 at 09:53

The limit of (Sin x)/x as x goes to 0 is still 1 even if degrees are used. You just get the extra pi/180 factor in the numerator and denominator and they cancel. This is easily seen by using L’Hospital’s rule.

LikeLike

Reply
- Lin McMullin says:
  
  September 18, 2018 at 13:11
  
  I don’t think so. By using (pi/180*x) in both the numerator and denominator you’ve changed the problem to radians and, yes, the limit is then 1. BUT you’ve changed the problem; it’s not the one you started with. With x in degrees d/dx(sin x) = (pi/180)cos(x) but the derivative of x is still 1, so the limit as x goes to 0 of sin(x)/x is (pi/180). You can verify this by Putting your grapher in DEGREE MODE and graphing. Zoom in and you will see the limit is pi/180 or about 0.017
  
  Look at the proof of d/dx(sin(x)) which is done in radians. If instead you use x in degrees you will see the factor of pi/180 in the part of the proof where the sector area formula (in degrees) is used.
  
  Another approach is to graph sin(x) and x separately. Look at the graph near the origin in radians and you will see the graphs are on top of each other and the y-coordinates are nearly the same; hence their ratio is 1 (as is the ratio of their slopes as per L’Hospital’s rule). If you then graph in degrees you will see the graphs and their slopes are quite different.
  
  HTH
  
  LikeLike
  
  Reply
Pingback: Why Radians? – Musings of a maths teacher
themannster says:

October 14, 2017 at 11:42

Reblogged this on The Maths Mann.

LikeLike

Reply
mrreja says:

July 10, 2017 at 06:26

Reblogged this on mrreja and commented:
হুম

LikeLike

Reply
sathasivam says:

September 3, 2016 at 23:57

Lin,can you explain how d(sinx)/dx where x in degree is 180(cosx)/pi

LikeLike

Reply
- Lin McMullin says:
  
  September 4, 2016 at 12:13
  
  Sathasivam
  It is not 180(cosx)/pi, rather pi*cos(x)/180.
  
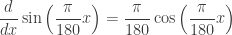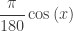  1. If x is in degrees, then to differentiate a trig function you must change the degrees to radians. So with x in degrees $\displaystyle \sin \left( x \right)=\sin \left( \frac{\pi }{180}x \right)$ with the argument now in radians. Then differentiate $\displaystyle \frac{d}{dx}\sin \left( \frac{\pi }{180}x \right)=\frac{\pi }{180}\cos \left( \frac{\pi }{180}x \right)$ or $\displaystyle \frac{\pi }{180}\cos \left( x \right)$ returning the argument to degrees.
  
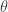  2. If you wanted to work entirely in degrees from the start, then the middle term of the inequality in the post would be $\displaystyle \frac{2\pi \theta }{360}$ using the formula for arc length with $\theta$ in degrees. Then the 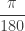$\displaystyle \frac{\pi }{180}$ will work its way through the inequalities resulting in $\displaystyle \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \left( \theta \right)}{\theta }=\frac{\pi }{180}$ and from there into the derivative formulas.
  
  3. Try graphing $y=\sin \left( x \right)$ with x in degrees and your calculator set to degree mode. In a square window (that is, with equal units on both axes) the graph will appear to be very flat – almost linear. Thus, you would expect the slopes (derivatives) to be much smaller than when working in radians. The factor $\displaystyle \frac{\pi }{180}\approx 0.001745...$ takes care of that “flattening.”
  
  LikeLike
  
  Reply
Pingback: What are Radians? Where Do They Come From? - Quirky Science
RJ Davis says:

December 14, 2015 at 21:30

Could you do this same example with Cos (x) instead of Sin (x)?

LikeLike

Reply
- Lin McMullin says:
  
  December 15, 2015 at 09:36
  
  Is this what you mean? With x in degrees you must change the argument to radians and then differentiate using the Chain Rule:
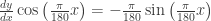
  $\frac{dy}{dx}\cos \left( \frac{\pi }{180}x \right)=-\frac{\pi }{180}\sin \left( \frac{\pi }{180}x \right)$
  This works the same way with any trig function.
  
  LikeLike
  
  Reply
  - RJ Davis says:
    
    December 15, 2015 at 10:11
    
    That is want I meant. I just wanted to make sure that the pi/180 would stay constant throughout and the chain rule would then be applicable. Thanks!
    
    LikeLike
Ranjay says:

December 7, 2014 at 02:49

Hi Lin,
I like the way you have explained for easy understanding. However, please expalain (or give reference) of the inequality you have used for the explanation.

LikeLike

Reply
- Lin McMullin says:
  
  December 7, 2014 at 12:30
  
  Hi Ranjay
  I have added an explanation of the inequality at the end of the post. Thanks for writing; you were probably not the only one who was wondering about this.
  
  LikeLike
  
  Reply
Jim says:

October 1, 2014 at 10:15

Yes, if one were to use anything other than radian measure than one would get constants popping up upon differentiating trig functions and once they appeared these constants would mestasize. For the same reason one uses e as exponential base rather than the seemly more simple choice of say 10. Differentiating 10^x and the constant ln(10) appears. This must be nipped in the bud.

In elementary geometry where one is not using calculus the use of degrees or grads is perfectly OK.

LikeLike

Reply
Bill Mahanna 6908 23 Ave W.,Bradenton, FL 34209 says:

August 1, 2013 at 08:51

The radian is a linear measure of an angle, and it works best if you have your delta x and delta y in the same units. Degrees are a made up unit. Try plotting a sine wave using radians vs degrees for the x-axis. The y-axis will be the amplitude. A linear measurement. I’m sure more could be said but this might get your foot in the door.
Bill Retired math/physics teacher

LikeLike

Reply
Steve Pulford says:

October 22, 2012 at 18:59

Hi Lin,
Small typo – “a unit circles is a circle…”
Love your stuff!
Steve

LikeLike

Reply
- Lin McMullin says:
  
  October 22, 2012 at 19:01
  
  Thanks. I fixed it. Glad you like the blog.
  
  LikeLike
  
  Reply