Author Archives: Lin McMullin

The Calculus of Inverses

Posted on by
3

Today we will consider computing the derivative of the inverse of a function. This is pretty standard and is in all the textbooks.

The usual suspects are the inverse trigonometric functions. So let’s start with y={{\sin }^{-1}}\left( x \right) and then rewrite this as x=\sin \left( y \right). Differentiating this gives

\displaystyle 1=\cos \left( y \right)\frac{dy}{dx}
\displaystyle \frac{dy}{dx}=\frac{1}{\cos \left( y \right)}

Since we would like this in terms of x we can proceed two ways.

The denominator is the cosine of the number whose sine is x. So using the relationship

\cos \left( y \right)=\sqrt{1-{{\sin }^{2}}\left( y \right)}=\sqrt{1-{{x}^{2}}}

we find that

\displaystyle \frac{dy}{dx}=\frac{1}{\sqrt{1-{{x}^{2}}}}.

That tends to be confusing so another method is to draw a right triangle with an acute angle of y and arrange the side so that

\displaystyle \sin \left( y \right)=\frac{x}{1}=\frac{\text{opposite}}{\text{hypotenuse}}


From this we can find all the trigonometric functions of y, specifically:

\displaystyle \cos \left( y \right)=\frac{\text{adjacent}}{\text{hypotenuse}}-\frac{\sqrt{1-{{x}^{2}}}}{1}=\sqrt{1-{{x}^{2}}} and \displaystyle \frac{dy}{dx}=\frac{1}{\sqrt{1-{{x}^{2}}}}.

A second example: Find the derivative of y={{\sec }^{-1}}\left( x \right). The domain of this function is \left| x \right|\ge 1 and the range is [0,\tfrac{\pi }{2})\cup (\tfrac{\pi }{2},\pi ], the function is increasing on both parts of its domain; we will need to know this.

Proceeding as above we will find that

\displaystyle \frac{dy}{dx}=\frac{1}{\sec \left( y \right)\tan \left( y \right)}.

Drawing a triangle as above and arranging the side so that sec(y) = x:

Then \displaystyle \frac{dy}{dx}=\frac{1}{x\sqrt{1+{{x}^{2}}}},

But wait! It may be that x < 0, but {{\sec }^{-1}}\left( x \right) is increasing and the derivative should always be positive. So, this needs to be adjusted to

\displaystyle \frac{d}{dx}{{\sec }^{-1}}\left( x \right)=\frac{1}{\left| x \right|\sqrt{1+{{x}^{2}}}}

These can be a bit tricky.

Next: the fifth and last posting in this series will look at the graphical and numerical aspects of the derivatives of a function and its inverse.

The Range of the Inverse

Posted on by
Reply

The last two post discussed inverse functions and some concerns about them. We continue that today be considering that fact that sometimes the inverse of a function is not a function, and what can be done in that case.

Since the square of both 3 and –3 is 9. Which number should you get when you unsquare 9? Is the result, 3 or –3?

Mathematicians want, for practical reasons, inverses to be functions. If the original function is not strictly monotonic then the inverse will not be a function. That is, if there are places on the original function that have the same y-values then the inverse (set of ordered pairs found by reversing the function’s ordered pairs) will not be a function. If some horizontal line intersects the graph of the function more than once, the inverse will not be a function.

While it may seem a bit too convenient, what is done is that the range of the inverse is restricted so that the inverse is a function. So for f (x) = x2 the range of the inverse is restricted to non-negative values. So f -1(9) = 3 and f -1(10) = \sqrt{10}  where it is understood that this represents a non-negative number. This is why {{f}^{-1}}\left( {{a}^{2}} \right)=\sqrt{{{a}^{2}}}=\left| a \right|. So that if a = –4, \sqrt{{{a}^{2}}}=\left| -4 \right|=4.

The restriction is arbitrary. It would be just as possible to make the range all non-positive numbers. While arbitrary, the restriction is not unreasonable. After all, once we understand this, we can easily find the other value if we need it. This is also necessary for calculators to work; the process they use to compute the value can only return one value. The (restricted) ranges of the common functions are what mathematicians feel are the most useful.

None of the trigonometric functions pass the horizontal line test; none of their inverses are functions until the ranges have been restricted. These restrictions are in the textbooks. For example: The domain of sin-1(x) is -1\le x\le 1, these are the output values of the sin(x); the range is restricted to \displaystyle -\tfrac{\pi }{2}\le {{\sin }^{-1}}\left( x \right)\le \tfrac{\pi }{2}. Because the signs of the trig functions are different outside of the first quadrant and in order to make as many of the inverses as possible continuous, each inverse trig function has a different range. You will find these in your textbook. They are built into calculators and computers. This can be a little confusing for students, but there is not much that can be done about that.

This is the third of 5 posts on inverses. The next post: The Calculus of Inverses.

Writing Inverses

Posted on by
Reply

In my last post I identified two “problems” related to inverses. The first of these is that there may be no string of operations, no algebra or arithmetic, which tells us how to evaluate the inverse function.

For simple functions you can find the inverse function by switching the x and the y and then solving for y. If you can do that, this produces a nice expression for the inverse. Alas usually you cannot do that.

What to do?

What you can do is invent a name and/or a symbol for the new function. So if f(x) = x2, we write f -1(x) = \sqrt{x} and we think we have solved the problem. We have not. While I can write \sqrt{x}, what arithmetic can I do to express this number as a decimal? There is an algorithm for this; (you can find it on the internet by searching for “square root algorithm”). You can use a calculator or look in a table as we did back in the “old days.” But that is not the same as performing a series of arithmetic or algebraic operations.

And if \sqrt{10} does not slow you down, how about sin-1(0.12345)? The only hope in some cases is to try to solve something like x2 = 10 or sin(y) = 0.12345, not much hope there. We are left with using technology of some sort if we need a number (decimal); calculators have buttons for square roots and inverse sines. But sometimes writing \sqrt{10} or  sin-1(0.12345) is good enough.

Making up a new function or symbol to “solve” a problem, even if that function cannot be written as a string of operations is actually fairly common. The sin(x) is defined as the y-coordinate of a point on the unit circle. Except for some special numbers you cannot find y-coordinates that easily. You have seen others already. All the trigonometric functions and their inverses as well as logarithmic functions are of this sort. Mathematics is full of them.

The next post will discuss the other problem: the inverse of a function may not be a function. Since there are two numbers whose square is 9, what is the “unsquare” of 9; is it 3 or –3?

This is the second of 5 posts on inverses.

Inverses

Posted on by
Reply

The next few posts will concern functions and their inverses. Today we will just get into the basics which, hopefully, students know from their work prior to calculus. Of course, they will have forgotten some of this and claim they never learned it. (Which may be correct, but one hopes they were taught it.) This is one of the places where a brief review just before teaching the calculus of inverses might be useful.

When starting out with functions we are given a value of the input or independent variable, x, and are asked to compute the output value or the dependent variable, y. Then, to mix things up, you may be given an output value and asked to find the input value that produces it. With the beginning functions this is not too difficult; that is, there are algebraic techniques that can be used. If you have to do a number of these, you can easily write an expression solved for x that you can use to find the y’s.

To streamline all this mathematicians use the concept of the inverse of a function. If a function is a set of ordered pairs (a, b) or (x, f (x)) then the inverse is defined as the set with these ordered pairs with the coordinates reversed; (b, a) or (f (x), x). Since this last looks a bit strange we define a new notation f -1(x) to denote the inverse of f(x). That is f -1(x) is the inverse function of the original function f(x). The ordered pairs are now (x, f -1(x)).

For very simple functions the inverse can be found by switching the x and y in the original and the solving for y. So if f (x) = 2x + 3 we write x = 2y + 3 and solve to get y = ½(x – 3). So f -1(x) = (½)(x– 3).

Notice that f (f -1(x)) = 2(½(x – 3))+3 = x.

Several things to note at this point:

  • Inverses occur in pairs. The inverse of the inverse is the original function.
  • The inverse undoes whatever the function did and returns the original input value. In symbols this is  f -1(f (x)) = f (f -1(x))=x.
  • The points (a, b) and (b, a) are symmetric to the line y = x and therefore the inverse of a function has a graph that is the reflection of the function’s graph across the line y = x. The function and its inverse are symmetric to this line.
  • The domain and range switch places: the domain of the inverse is the range of the function, and the range of the inverse is the domain of the function.

There are also several problems that need to be addressed.

  • There may be no string of operations, no “algebra”, which will produce the output for the inverse function. We cannot write an algebraic expression to find the number whose seventh power is 10. What do we do in this case?
  • The inverse of a function may not be a function. Since there are two numbers whose square is 9, what is the “unsquare” of 9; is it 3 or –3? When does this happen? Since it is really useful for the inverse to be a function, what can be done about this?

These two “problems” will be the subjects of my next two post.

(This started out as one post and has grown to a series 5.)

Open or Closed?

Posted on by
2

About this time of year you find someone, hopefully one of your students, asking, “If I’m finding where a function is increasing, is the interval open or closed?”

Do you have an answer?

This is a good time to teach some things about definitions and theorems.

The place to start is to ask what it means for a function to be increasing. Here is the definition:

A function is increasing on an interval if, and only if, for all (any, every) pairs of numbers x1 < x2 in the interval, f(x1) < f(x2).

(For decreasing on an interval, the second inequality changes to f(x1) > f(x2). All of what follows applies to decreasing with obvious changes in the wording.)

  1. Notice that functions increase or decrease on intervals, not at individual points. We will come back to this in a minute.
  2. Numerically, this means that for every possible pair of points, the one with the larger x-value always produces a larger function value.
  3. Graphically, this means that as you move to the right along the graph, the graph is going up.
  4. Analytically, this means that we can prove the inequality in the definition.

For an example of this last point consider the function f(x) = x2. Let x2 = x1 + h where h > 0. Then in order for  f(x1) < f(x2) it must be true that

{{x}_{1}}^{2}<{{\left( {{x}_{1}}+h \right)}^{2}}
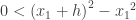
0<{{\left( {{x}_{1}}+h \right)}^{2}}-{{x}_{1}}^{2}
0<{{x}_{1}}^{2}+2h{{x}_{1}}+{{h}^{2}}-{{x}_{1}}^{2}
0<h\left( 2{{x}_{1}}+h \right)

This can only be true if 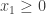{{x}_{1}}\ge 0, Thus, x2 is increasing only if x\ge 0.

Now, of course, we rarely, if ever, go to all that trouble. And it is even more trouble for a function that increases on several intervals.  The usual way of finding where a function is increasing is to look at its derivative.

Notice that the expression {{\left( {{x}_{1}}+h \right)}^{2}}-{{x}_{1}}^{2} looks a lot like the numerator of the original limit definition of the derivative of x2 at x = x1, namely \displaystyle {f}'\left( {{x}_{1}} \right)=\underset{h\to 0}{\mathop{\lim }}\,\frac{{{\left( {{x}_{1}}+h \right)}^{2}}-{{x}_{1}}^{2}}{h}. If h > 0, where the function is increasing the numerator is positive and the derivative is positive also. Turning this around we have a theorem that says, If 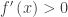{f}'\left( x \right)>0 for all x in an interval, then the function is increasing on the interval. That makes it much easier to find where a function is increasing: we simplify find where its derivative is positive.

There is only a slight problem in that the theorem does not say what happens if the derivative is zero somewhere on the interval. If that is the case, we must go back to the definition of increasing on an interval or use some other method. For example, the function x3 is increasing everywhere, even though its derivative at the origin is zero.

Let’s consider another example. The function sin(x) is increasing on the interval \left[ -\tfrac{\pi }{2},\tfrac{\pi }{2} \right] (among others) and decreasing on \left[ \tfrac{\pi }{2},\tfrac{3\pi }{2} \right]. It bothers some that \tfrac{\pi }{2} is in both intervals and that the derivative of the function is zero at x = \tfrac{\pi }{2}. This is not a problem. Sin(\tfrac{\pi }{2}) is larger than all the other values is both intervals, so by the definition, and not the theorem, the intervals are correct.

It is generally true that if a function is continuous on the closed interval [a,b] and increasing on the open interval (a,b) then it must be increasing on the closed interval [a,b] as well. (There is a proof by Lou Talman of this fact click here .)

Returning to the first point above: functions increase or decrease on intervals not at points. You do find questions in books and on tests that ask, “Is the function increasing at x = a.” The best answer is to humor them and answer depending on the value of the derivative at that point. Since the derivative is a limit as h approaches zero, the function must be defined on some interval around x = a in which h is approaching zero. So answer according to the value of the derivative on that interval.

You can find more on this here.

Case Closed.

Far Out!

Posted on by
1

A monster problem for Halloween.

A while ago I suggested you look at \displaystyle \underset{x\to \infty }{\mathop{\lim }}\,\frac{\ln \left( {{x}^{5}} \right)}{{{x}^{0.02}}} , which using the dominance idea is zero. Of course your students may try graphing or a table. Here’s the graph done by a TI-Nspire CAS. Note the scales.

This is not the way to go. Since the function is increasing near the origin, but the limit at infinity is zero there must be a maximum point where the function starts decreasing. And as the expression can never be negative once x > 1, there must be a point of inflection where the graph becomes concave up and can thereafter approach the x-axis from above as a horizontal asymptote. The maximum can be found by hand which makes for some great algebra manipulation practice:

\displaystyle \frac{d}{dx}\left( \frac{\ln \left( {{x}^{5}} \right)}{{{x}^{0.02}}} \right)=\frac{{{x}^{0.02}}\tfrac{5{{x}^{4}}}{{{x}^{5}}}-\ln \left( {{x}^{5}} \right)\left( 0.02{{x}^{-0.98}} \right)}{{{x}^{0.04}}}

\displaystyle \frac{d}{dx}\left( \frac{\ln \left( {{x}^{5}} \right)}{{{x}^{0.02}}} \right)=\frac{{{x}^{-0.98}}\left( 5-\left( 0.10 \right)\ln \left( x \right) \right)}{{{x}^{0.04}}}=\frac{50-\ln \left( x \right)}{10{{x}^{1.02}}}

Setting this equal to zero and solving gives x={{e}^{50}}\approx 5.185\times {{10}^{21}}

The second derivative is \displaystyle \frac{{{d}^{2}}}{d{{x}^{2}}}\left( \frac{\ln \left( {{x}^{5}} \right)}{{{x}^{0.02}}} \right)=\frac{-510+10.2\ln \left( x \right)}{100{{x}^{2.02}}}

and is zero when x = \displaystyle {{e}^{\frac{520}{10.2}}}\approx 1.382\times {{10}^{22}}

Okay, I skipped a few steps here, but you can challenge your students with that. Since we’re really interested in the solution here more than the solving ,this is really a good place to use a CAS calculator.

The first line in the figure above defines the function to save typing it each time. The second line finds the x-coordinate of the maximum point (how do we know this is a maximum?) and the third finds the x-coordinate of the point of inflection.  Much simpler this way!

Take a minute to consider the numbers. They are BIG! In fact, if the units on our graph paper are centimeters, then the maximum point is a little over 5,480 light-years away from the origin! The point of inflection is about 2.665 times farther at more than 14,607 light-years away!

Meanwhile the maximum value is only 91.9699 cm. That’s right centimeters, less than a meter. And the y-coordinate of the point of inflection is about 91.9524 cm. A drop of 0.0175 cm. in a horizontal distance of a little over 9,127 light-years.

Some problems are a lot less scary if done with technology.

Real “Real-life” Graph Reading

Posted on by
Reply

A few days ago, Paul Krugman wrote a blog about the job situation in the US.   Evan J. Romer, a mathematics teacher from Conklin, NY, used it as the basis for a great exercise on reading the graph of the derivative, the subject of my last post. He posted the questions to the AP Calculus Learning Community.  I liked them so much I have included them on my blog with Evan’s kind permission. The questions and solutions are here and on the Resources Tab above.

He used the graph below which shows the change in the number of non-farm jobs per month; in other words, the graph of a derivative of the number of people employed. The jagged graph is the data; the smooth graph is a model approximating the data.

The model is \displaystyle C\left( t \right)=\frac{1000{{t}^{2}}}{{{t}^{2}}+40}-800

From this Mr. Romer developed a series of questions very similar to AP questions.  Don’t overlook the last note which discusses a “classic AP calculus mistake” made by the first person to reply to Krugman’s blog.

The first of Romer’s questions are integration questions, which you may not yet have gotten to with your class. Below is another graph of nearly the same data displayed as a bar graph. (Around February 2010 this was dubbed the “Bikini Graph” – if you look at the graph before that date you will see why.) It may be helpful in explaining the first of Romer’s questions to your class since each bar represents the change in the number of jobs for that month and leads into the concept of accumulation and the integral as the area between the graph and the axis. You can return to this when you introduce integration.

Thank You Evan.