Good Question 12 – Parts with a Constant?

Posted on December 13, 2016 by Lin McMullin

Someone asked me about this a while ago and I thought I would share it with you. It may be a good question to get your students thinking about; see if they can give a definitive answer that will, of course, include a justification.

Integration by Parts is summarized in the equation

$\displaystyle \int_{{}}^{{}}{udv}=uv-\int_{{}}^{{}}{vdu}$

To use the equation, you choose part of a given integral (left side) to be u and part to be dv, both functions of x. Then you differentiate u and integrate dv and use them on the right side to obtain a simpler integral that you can integrate.

The question is this: When you integrate dv, should you, can you, have a constant of integration, the “+ C ” that you insist upon in other integration problems? Why don’t you use it here? Or can you?

Scroll down for my answer.

Answer: Let’s see what happens if we use a constant. Assume that $\displaystyle \int_{{}}^{{}}{dv}=v+C$ . Then

$\displaystyle \int_{{}}^{{}}{udv}=u\cdot \left( v+C \right)-\int_{{}}^{{}}{\left( v+C \right)du}$

$\displaystyle =uv+Cu-\left( \int_{{}}^{{}}{vdu}+\int_{{}}^{{}}{Cdu} \right)$

$\displaystyle =uv+Cu-\int_{{}}^{{}}{vdu}-Cu$

$\displaystyle =uv-\int_{{}}^{{}}{vdu}$

So, you may use a constant if you want, but it will always add out of the expression.

For more on integration by parts see here for the basic idea, here for the tabular method, here for a quicker way than the tabular method, and here for more on the tabular method and reduction formulas.

Subtract the Hole from the Whole.

Posted on December 6, 2016 by Lin McMullin

Sometimes I think textbooks are too rigorous. Behind every Riemann sum is a definite integral. So, authors routinely show how to solve an application of integration problem by developing the method starting from the Riemann sum and proceeding to an integral that give the result that is summarized in a “formula.” There is nothing wrong with that except that often the formula is all the students remember and are lost when faced with a similar situation that the formula does not handle. .

The volume of solid figure problems are developed from the idea that if a solid figure has a regular cross-section (that is, when cut perpendicular to a line, each face is similar – in the technical sense – to all the others). They are all squares, or equilateral triangles, or whatever. The last shape considered is usually a “washer”, that is, an annulus or two concentric circles. This is formed by revolving the region between two curves around a line. Authors develop a formula for such volumes: $\displaystyle \pi \int_{a}^{b}{{{\left( R\left( x \right) \right)}^{2}}-{{\left( r\left( x \right) \right)}^{2}}dx}$ .

Now there is nothing wrong with that, but I like to give the students their chance to show off. They can usually figure out the answer without Riemann sums. Here is my suggestion. After students have had some practice with circular cross-sections (“Disk” method”) I give them a series of three volumes to find.

Example 1: The curve $f\left( x \right)=\sin \left( \pi x \right)$ on the interval [0, ½] is revolved around the x-axis to form a solid figure. Find the volume of this figure.

Solution: $\displaystyle V=\int_{0}^{1}{\pi {{\left( \sin \left( \pi x \right) \right)}^{2}}dx}=\frac{\pi }{4}$

Example 2: The curve $g\left( x \right)=8{{x}^{3}}$ on the interval [0, ½] is revolved around the x-axis to form a solid figure. Find the volume of this figure.

Solution: $\displaystyle V=\int_{0}^{1/2}{\pi {{\left( 8{{x}^{3}} \right)}^{2}}dx=}\frac{\pi }{14}$

These they find easy. Then, leaving the first two examples in plain view, I give them:

Example 3: The region in the first quadrant between the graphs of $f\left( x \right)=\sin \left( \pi x \right)$ and $g\left( x \right)=8{{x}^{3}}$ is revolved around the x-axis. Find the volume of the resulting figure.

A little thinking and (rarely) a hint and they have it. $\displaystyle V=\frac{\pi }{4}-\frac{\pi }{14}$

What did they do? Easy, they subtracted the hole from the whole. We discuss this and why they think it is correct. We try one or two others. And now they are set to do any “washer” method problem without another formula to memorize.

Extensions:

1. In symbols, when rotation around a horizontal line, if R(x) is the distance from the curve farthest from the line of rotation and r(x) the distance from the closer curve to the line of rotation the result can be summarized in the formula

$\displaystyle V = \int_{a}^{b}{\pi {{\left( R\left( x \right) \right)}^{2}}dx}-\int_{a}^{b}{\pi {{\left( r\left( x \right) \right)}^{2}}dx}$ .

Notice, that I like to keep the $\pi$ inside the integral sign so that each integrand looks like the formula for the area of a circle. What the students need to know is to subtract the volume hole from the outside volume. With that idea and the disk method they can do any volume by washers problem.

2. You should show the students how this equation above can be rearranged into the formula in their books,

$\displaystyle V = \pi \int_{a}^{b}{{{\left( R\left( x \right) \right)}^{2}}-{{\left( r\left( x \right) \right)}^{2}}dx}$ .

This is so that they understand that the formulas are the same, and not think you’ve forgotten to tell them something important. It is also a good exercise in working with the notation. (see MPAC 5 – Notational fluency)

3. Next discuss what ${{\left( \pi R\left( x \right) \right)}^{2}}-\pi {{\left( r\left( x \right) \right)}^{2}}$ is the area of and how it relates to this problem. See if the students can understand what the textbook is doing; what shape the book is using.. Discuss the Riemann sum approach. (MPAC 1 Reasoning with definitions and theorems, and MPAC 5 Notational fluency)

4. With the idea of subtracting the “hole” try a problem like this. Example 4: The region in the first quadrant between x-axis and the graphs of $f\left( x \right)=\sqrt{x}$ and $g\left( x \right)=\sqrt{2x-4}$ is revolved around the x-axis. Find the volume of the resulting figure.

Solution: $\displaystyle V=\int_{0}^{4}{\pi {{\left( \sqrt{x} \right)}^{2}}dx}-\int_{2}^{4}{\pi {{\left( \sqrt{2x-4} \right)}^{2}}dx}=4\pi$

(Notice the limits of integration.)

Traditionally, this is done by the method of cylindrical shells, but you don’t need that. You could divide the region into two parts with a vertical line at x = 2 and use disks on the left and washers on the right, but you don’t need to do that either. Just subtract the hole from the whole.

Good Question 11 – Riemann Reversed

Posted on November 29, 2016 by Lin McMullin

Good Question 11 – or not.

The question below appears in the 2016 Course and Exam Description (CED) for AP Calculus (CED, p. 54), and has caused some questions since it is not something included in most textbooks and has not appeared on recent exams. The question gives a Riemann sum and asks for the definite integral that is its limit. Another example appears in the 2016 “Practice Exam” available at your audit website; see question AB 30. This type of question asks the student to relate a definite integral to the limit of its Riemann sum. These are called reversal questions since you must work in reverse of the usual order. Since this type of question appears in both the CED examples and the practice exam, the chances of it appearing on future exams look good.

To the best of my recollection the last time a question of this type appeared on the AP Calculus exams was in 1997, when only about 7% of the students taking the exam got it correct. Considering that by random guessing about 20% should have gotten it correct, this was a difficult question. This question, the “radical 50” question, is at the end of this post.

Example 1

Which of the following integral expressions is equal to $\displaystyle \underset{n\to \infty }{\mathop{\lim }}\,\sum\limits_{k=1}^{n}{\left( \sqrt{1+\frac{3k}{n}}\cdot \frac{1}{n} \right)}$ ?

There were 4 answer choices that we will consider in a minute.

The first key to answering the question is to recognize the limit as a Riemann sum. In general, a right-side Riemann sum for the function f on the interval [a, b] with n equal subdivisions, has the form:

$\displaystyle \underset{n\to \infty }{\mathop{\lim }}\,\sum\limits_{k=1}^{n}{\left( f\left( a+\frac{b-a}{n}\cdot k \right)\cdot \frac{b-a}{n} \right)}=\int_{a}^{b}{f\left( x \right)dx}$

To evaluate the limit and express it as an integral, we must identify, a, b, and f. I usually begin by looking for $\displaystyle \frac{b-a}{n}$ . Here $\displaystyle \frac{b-a}{n}=\frac{1}{n}$ and from this conclude that b – a = 1, so b = a + 1.

Usually, you can start by considering a = 0 , which means that the 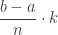$\displaystyle \frac{b-a}{n}\cdot k$ becomes the “x.”. Then rewriting the radicand as $\displaystyle 1+3\frac{1}{n}k=1+3\left( a+\frac{1}{n}\cdot k \right)$ , it appears the function is $\sqrt{1+3x}$ and the limit is $\displaystyle \int_{0}^{1}{\sqrt{1+3x}}dx=\frac{14}{9}$ .

The answer choices are

(A) $\displaystyle \int_{0}^{1}{\sqrt{1+3x}}dx$ (B) $\displaystyle \int_{0}^{3}{\sqrt{1+x}}dx$ (C) $\displaystyle \int_{1}^{4}{\sqrt{x}}dx$ (D) $\displaystyle \tfrac{1}{3}\int_{0}^{3}{\sqrt{x}}dx$

The correct choice is (A), but notice that choices B, C, and D can be eliminated as soon as we determine that b = a + 1. That is not always the case.

Let’s consider another example:

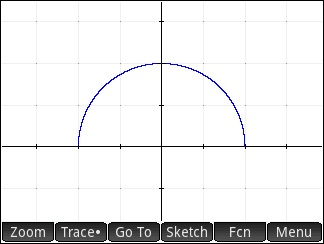
Example 2: $\displaystyle \underset{n\to \infty }{\mathop{\lim }}\,\sum\limits_{k=1}^{n}{\left( {{\left( 2+\frac{3}{n}k \right)}^{2}}\left( \frac{3}{n} \right) \right)}=$

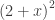As before consider $\displaystyle \frac{b-a}{n}=\frac{3}{n}$ , which implies that b = a + 3. With a = 0, the function appears to be ${{\left( 2+x \right)}^{2}}$ on the interval [0, 3], so the limit is $\displaystyle \int_{0}^{3}{{{\left( 2+x \right)}^{2}}}dx=39$

BUT

What if we take a = 2? If so, the limit is $\displaystyle \int_{2}^{5}{{{x}^{2}}dx}=39$ .

And now one of the “problems” with this kind of question appears: the answer written as a definite integral is not unique!

Not only are there two answers, but there are many more possible answers. These two answers are horizontal translations of each other, and many other translations are possible, such as 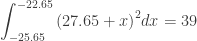$\displaystyle \int_{-25.65}^{-22.65}{{{\left( 27.65+x \right)}^{2}}dx}=39$ .

The same thing can occur in other ways. Returning to example 1,and using something like a u-substitution, we can rewrite the original limit as $\displaystyle \frac{1}{3}\cdot \underset{n\to \infty }{\mathop{\lim }}\,\sum\limits_{k=1}^{n}{\left( \sqrt{1+\frac{3k}{n}}\cdot \frac{3}{n} \right)}$ .

Now b = a + 3 and the limit could be either 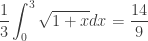$\displaystyle \frac{1}{3}\int_{0}^{3}{\sqrt{1+x}}dx=\frac{14}{9}$ or $\displaystyle \frac{1}{3}\int_{1}^{4}{\sqrt{x}}dx=\frac{14}{9}$ , among others.

My opinions about this kind of question.

The real problem with the answer choices to Example 1 is that they force the student to do the question in a way that gets one of the answers. It is perfectly reasonable for the student to approach the problem a different way, and get a different correct answer that is not among the choices. This is not good.

The problem could be fixed by giving the answer choices as numbers. These are the numerical values of the 4 choices:(A) 14/9 (B) 14/3 (C) 14/3 (D) 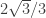$2\sqrt{3}/3$ . As you can see that presents another problem. Distractors (wrong answers) are made by making predictable calculus mistakes. Apparently, two predictable mistakes give the same numerical answer; therefore, one of them must go.

A related problem is this: The limit of a Riemann sum is a number; a definite integral is a number. Therefore, any definite integral, even one totally unrelated to the Riemann sum, which has the correct numerical value, is a correct answer.

I’m not sure if this type of question has any practical or real-world use. Certainly, setting up a Riemann sum is important and necessary to solve a variety of problems. After all, behind every definite integral there is a Riemann sum. But starting with a Riemann sum and finding the function and interval does not seem to me to be of practical use.

The CED references this question to MPAC 1: Reasoning with definitions and theorems, and to MPAC 5: Building notational fluency. They are appropriate,and the questions do make students unpack the notation.

My opinions notwithstanding, it appears that future exams will include questions like these.

These questions are easy enough to make up. You will probably have your students write Riemann sums with a small value of n when you are teaching Riemann sums leading up to the Fundamental Theorem of Calculus. You can make up problems like these by stopping after you get to the limit, giving your students just the limit, and having them work backwards to identify the function(s) and interval(s). You could also give them an integral and ask for the associated Riemann sum. Question writers call questions like these reversal questions since the work is done in reverse of the usual way.

Here is the question from 1997, for you to try. The answer is below.

Answer B. Hint n = 50

Revised 5-5-2022

Graphing Integrals

Posted on November 15, 2016 by Lin McMullin

The sixth in the Graphing Calculator / Technology series

The topic of integration is coming up soon. Here are some notes and ideas about the integration operation on graphing calculators. The entries are the same or very similar for all calculator brands.

The basic problem of evaluating a definite integral on a graphing calculator is done without finding an antiderivative; that is, the calculator uses a numerical algorithm to produce the result. The calculator provides a template,and you fill in the 4 squares so that the expression looks exactly like what you write by hand. Then the calculator computes the result. (Older models require a one-line input requiring, in order, the integrand, the independent variable, the lower limit of integration and the upper limit in that order, separated by commas.) The first interesting thing is that the variable in the integrand does to have to be x. As the first figure illustrates using x or a or any other letter gives the same result.

This is because the variable of integration is just a place holder. Sometimes called a “dummy variable”, this letter can be anything at all, including x. On the home or calculation screen you might as well always use x, so the entry will look like what you have on your paper. As we will see, when graphing it may be less confusing to use a different letter.

The antiderivative, F, of any function, f, can be written as a function defined by an integral where there is a point on the antiderivative of f , which is with F ’ = f. The point (a, F(a)) is the initial condition. (In the following we will use F(a) = 0 as the initial condition – the graph will contain the origin. As a further investigation, try changing the lower limit to different numbers and see how that changes the graph.)

The integration operation can be used to graph the antiderivative of a function without finding the antiderivative. You may graph the antiderivative when teaching antiderivatives. Have students look at the graph of the antiderivative and guess what that function is.

When graphing use x as the upper limit of integration and a different letter for the variable in the rest of the template. The calculator will use different values of x to calculate the points to be graphed.

The set-up shown in the next figure shows how to enter a function defined by an integral (blue line) and the same function obtained by antidifferentiating (red squares). As you can see the results are the same.

In this way, you can explore the functions and their indefinite integrals by graphing.

The Fundamental Theorem of Calculus

Another use of using the graph of an integral is to investigate both parts of the Fundamental Theorem of Calculus (FTC). Roughly speaking, the FTC says that the integral of a derivative of a function is that function, and the derivative of an integral is the integrand.

In the figure below, the same function is entered both ways; the graphs are the same. (Note the x’s in the second line must be x in all four places.)

Good Question 10 – The Cone Problem

Posted on November 8, 2016 by Lin McMullin

Today’s good question is an optimization problem, but its real point is choosing how to do the computation. As such it relates to MPAC 3a and 3b: “Students can … select appropriate mathematical strategies [and] sequence algebraic/computational processes logically.” The algebra required to solve this questions can be quite daunting, unless you get clever. Here’s the question.

A sector of arc length x is removed from a circle of radius 10 cm. The remaining part of the circle is formed into a cone of radius r and height h,

Find the value of x so that the cone has the maximum possible volume.

The sector that was removed is also formed into a cone. Find the value of x that makes this cone have it maximum possible volume. (Hint: This is an easy problem.)

In the context of the problem, the expression for the volume of the cone in part a. has a domain of $0\le x\le 20\pi$ . Why? Ignore the physical situation and determine the domain of the expression for the volume from a. Graph the function. Discuss.

Solutions:

Part a: As usual, we start by assigning some variables.

Let r be the radius of the base of the cone and let h be its height. The circumference of the cone is $2\pi r=20\pi -x$ , so $r=10-\frac{x}{2\pi }$ and $h=\sqrt{{{10}^{2}}-{{r}^{2}}}$ . The volume of the cone is

$\displaystyle V=\frac{\pi }{3}{{r}^{2}}h=\frac{\pi }{3}{{r}^{2}}\sqrt{{{10}^{2}}-{{r}^{2}}}=\frac{\pi }{3}{{\left( 10-\frac{x}{2\pi } \right)}^{2}}\sqrt{{{10}^{2}}-{{\left( 10-\frac{x}{2\pi } \right)}^{2}}}$

To find the maximum, the next step is to differentiate the volume. The expression on the right above looks way complicated and its derivative will be even worse. Simplifying it is also a lot of trouble, and, in fact, does not make things easier.* Here’s where we can be clever and avoid a lot of algebra. Let’s just work from $\displaystyle V=\frac{\pi }{3}{{r}^{2}}\sqrt{{{10}^{2}}-{{r}^{2}}}$

To find the maximum differentiate the volume with respect to x using the chain rule.

$\displaystyle \frac{dV}{dx}=\frac{dV}{dr}\cdot \frac{dr}{dx}=\frac{\pi }{3}\left( {{r}^{2}}\frac{-2r}{2\sqrt{{{10}^{2}}-{{r}^{2}}}}+2r\sqrt{{{10}^{2}}-{{r}^{2}}} \right)\left( -\frac{1}{2\pi } \right)$

Setting this equal to zero and simplifying (multiply by $-6\sqrt{{{10}^{2}}-{{r}^{2}}}$ ) gives

$-{{r}^{3}}+2r\left( 100-{{r}^{2}} \right)=200r-3{{r}^{3}}=0$

$\displaystyle r=0,r=\sqrt{\frac{200}{3}}=\frac{10\sqrt{6}}{3}$

The minimum is obviously r = 0, so the maximum occurs when $\displaystyle r=10-\frac{x}{2\pi }=\frac{10\sqrt{6}}{3}$ . Then, solving for x gives

$\displaystyle x=2\pi \left( 10-\frac{10\sqrt{6}}{3} \right)\approx 11.52986$

Aside: We often see questions saying, if y = f(u) and u = g(x), find dy/dx. Here we have put that idea to practical use to save doing a longer computation.

Part b: The arc of the piece cut out is the circumference, x, of a cone with a radius of $\displaystyle {{r}_{1}}=\frac{x}{2\pi }$ and a height of $\displaystyle {{h}_{1}}=\sqrt{{{10}^{2}}-{{r}_{1}}^{2}}$ . Its volume is

$\displaystyle V=\frac{\pi }{3}{{r}_{1}}^{2}\sqrt{{{10}^{2}}-{{r}_{1}}^{2}}$

This is the same as the expression we used in part a. and can be handled the same way, except that here $\displaystyle \frac{d{{r}_{1}}}{dx}=+\frac{1}{2\pi }$ . The computation and result will be the same. The result will be the same. The maximum occurs at

$\displaystyle x=2\pi \left( 10-\frac{10\sqrt{6}}{3} \right)\approx 11.52986$

This should not be a surprise. The piece cut out and the piece that remains are otherwise indistinguishable, so the maximum volume should be the same for both.

Part c: From part a we have $\displaystyle V=\frac{\pi }{3}{{r}^{2}}\sqrt{{{10}^{2}}-{{r}^{2}}}=\frac{\pi }{3}{{\left( 10-\frac{x}{2\pi } \right)}^{2}}\sqrt{{{10}^{2}}-{{\left( 10-\frac{x}{2\pi } \right)}^{2}}}$ . To graph there is no need to simplify the expression in x:

$Tthe x scale marks are at multiples of $latex 5\pi $$

The x-scale marks are at multiples of $5\pi$

The domain is determined by the expression under the radical so

$-10\le r\le 10$

$-10\le 10-\frac{x}{2\pi }\le 10$

$0\le x\le 40\pi$

This is the “natural domain” of the function without regard to the physical situation given in the original problem. I cannot think of a reason for the difference.

________________

*Fully simplified in terms of x the volume is $\displaystyle V=\frac{1}{24{{\pi }^{2}}}{{\left( 20\pi -x \right)}^{2}}\sqrt{40\pi x-{{x}^{2}}}$ . This isn’t really easier to differentiate and solve.

From One Side or the Other.

Posted on November 1, 2016 by Lin McMullin

Recently, a reader wrote and suggested my post on continuity would be improved if I discussed one-sided continuity. This, along with one-sided differentiability, is today’s topic.

The definition of continuity requires that for a function to be continuous at a value x = a in its domain $\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=f\left( a \right)$ and that both values are finite. That is, the limit as you approach the point in question be equal to the value at that point. This limit is a two-sided limit meaning that the limit is the same as x approaches a from both sides. That definition is extended to open intervals, by requiring that for a function to be continuous on an open interval, that it is continuous at every point of the interval

How do you check every point? One way is to prove the limit in the definition in general for any point in the open interval. Another is to develop a list of theorems that allow you to do this. For example, f(x) = x can be shown to be continuous at every number. Then sums, differences, and products, of this function allows you to extend the property to polynomials and then other functions.

But what about a function that has a domain that is not the entire number line? Something like $f\left( x \right)=\sqrt{4-{{x}^{2}}},-2\le x\le 2$ . Here, $f\left( -2 \right)=f\left( 2 \right)=0$ ; the function is defined at the endpoints. A look at the graph shows a semi-circle that appears to contain the endpoints (–2, 0) and (2, 0). The function is continuous on the open interval (–2, 2) but cannot be continuous under the regular definition since the limit at the endpoints does not exist. The limit does not exist because the limit from the left at the left-endpoint, and the limit from the right at the right endpoint do not exist. What to do?

What is done is to require only that the one-sides limits from inside the domain exist. Here they do: $\underset{x\to -2+}{\mathop{\lim }}\,f\left( x \right)=0$ and the $\underset{x\to 2-}{\mathop{\lim }}\,f\left( x \right)=0$ and since the limits equal the values we say the function is continuous on the closed interval [–2, 2]. In general, when you say a function is continuous on a closed interval, you mean that the one-sided limits from inside the interval exist and equal the endpoint values.

You can determine that the limits exist by finding them as in the example above. Another way is to realize that if a < b < c < d and the function is continuous on the open (or closed) (a, d) then it is continuous on the closed interval [b c].

Why bother?

The reason we take this trouble is because for some reason the proof of the theorem under consideration requires that the endpoint value not only exist but hooks up with the function to make it continuous. Thus, the continuity on a closed interval is included in the hypotheses of theorem where this property is required. For example, the Intermediate Value Theorem would not work on a function that had no endpoints for $f\left( c \right)$ to be between. Also, the Mean Value Theorem requires you to find the slope between the endpoints, so the endpoint needs to be not only defined, but attached to the rest of the function.

One-sided differentiability

The definition of the derivative at a point also requires a two-sided limit to exist at the point. Most of the early theorems in calculus require only that the function be differentiable on an open interval.

Is it possible to define differentiability at the endpoint of an interval? Yes. It’s done in the same way by using a one-sided limit. If x = a is the left endpoint of an interval, then the derivative from the right at that point is defined as

$\displaystyle {f}'\left( a \right)=\underset{h\to 0+}{\mathop{\lim }}\,\frac{f\left( a+h \right)-f\left( a \right)}{h}$ .

By letting h approach 0 only from the right, you never consider values outside the interval. (At the right endpoint a similar definition is used with $h\to 0-$ ).

So why don’t we ever see one-sided derivatives? Because the theorems do not need them to prove their result. Hypotheses of theorems should be the minimum requirements needed, so if there is no need for the function to be differentiable at an endpoint, this is not listed in the hypotheses. This makes the hypothesis less restrictive and, therefore, covers more situations.

One theorem, beyond what is usually covered in beginning calculus, where endpoint differentiability is needed is Darboux’s Theorem. Darboux’s Theorem is sometime called the Intermediate Value Theorem for derivatives. It says that the derivative takes on all values between the derivatives at the endpoints, and thus needs the one-sided derivatives at the endpoints to exist. Interestingly, Darboux’s Theorem does not require the function to be continuous on the open interval between the endpoints.

MPAC 6 Communicating

Posted on October 25, 2016 by Lin McMullin

Saving the best, or perhaps the most important, until last, MPAC 6 is the verbal part of the Rule of Four. Problems and real-life situations are “translated” from ideas or words into symbols, equations, graphs, and tables where they are examined and manipulated to find solutions. Once the solutions are found, they must be communicated along with the reasoning involved. The aspects of good mathematical communications are those listed in this MPAC.

MPAC 6: Communicating

Students can:

a. clearly present methods, reasoning, justifications, and conclusions;

b. use accurate and precise language and notation;

c. explain the meaning of expressions, notation, and results in terms of a context (including units);

d. explain the connections among concepts;

e. critically interpret and accurately report information provided by technology; and

f. analyze, evaluate, and compare the reasoning of others.

— AP^® Calculus AB and AP^® Calculus BC Course and Exam Description Effective Fall 2016, The College Board, New York © 2016. Full text is here.

Justifying answers and explaining reasoning in words has long been required on AP calculus exams. The exams have also required students to explain the meaning of expression involving definite integrals and the value of a derivative in the context of the questions.

How/where can you make sure students use these ideas in your classes.

Since to write mathematics well textbook authors do the things listed under this MPAC, but they rarely require students to write about or explain mathematics. They do not show students how to write good explanations of their work and solutions nor, do they provide exercises requiring explanations. Therefore, teachers must do it.

When you get to the end of the year and start working on old AP calculus exams for review you find many questions requiring students to communicate their methods and reasoning, the meanings of their work and results, the connections among different concepts, interpreting what their technology has shown them.

But waiting until the end of the year is way too late. This kind of work should be included in students’ mathematical work from the beginning, before Algebra 1. It can and should be done at every level. By the time they get to calculus, students should not be at all surprised at being asked to explain verbally and in writing what they are doing and why they chose to do it that way.

Find or provide opportunities for students to consider the reasoning of others (MPAC 6f) as well as explain their reasoning to each other. This can be accomplished with group projects, study groups, checking each other’s work, etc. You can also provide templates hits and tips for writing well.The Course and Exam Description includes an entire section on “Representative Instructional Strategies” (pp. 33 – 37). Among the suggestions are various ways to have students work together and separately on improving their communication skills. The following section (pp. 37 – 38) discusses what a “quality response will include:

a logical sequence of steps
an argument that explains why those steps are appropriate, and
an accurate interpretation of the solution (with units) in the context of the situation”

Provide less than perfect answers for students to critique and improve. (Hint: Use the sample student responses that are released each year along with the exams to show good and not-so-good answers and reasoning.

When AP exam questions are written the writers reference them to the LOs, EKs and MPACs. The released 2016 Practice Exam given out at summer institutes this summer is in the new format and contains very detailed solutions for both the multiple-choice and free-response questions that include these references. (This version is not available online as far as I know.) None of the multiple-choice question, but all six free-response questions on both AB and BC exam reference MPAC 6 (although see 2014 AB 18 for an idea of how MPAC 6f may be tested).

Here are some previous posts on these subjects:

Teaching How to Read Mathematics

Writing on the AP Calculus Exams

The Opposite of Negative

What’s a Mean Old Average Anyway?

Others

PLEASE NOTE: I have no control over the advertising that appears on this blog. It is provided by WordPress and I would have to pay a great deal to not have advertising. I do not endorse anything advertised here. I noticed that ads for one of the presidential candidates occasionally appears; I certainly do not endorse him.

Teaching Calculus

The pleasure lies not in discovering the truth, but in searching for it.

Author Archives: Lin McMullin

Good Question 12 – Parts with a Constant?

Subtract the Hole from the Whole.

Good Question 11 – Riemann Reversed

Graphing Integrals

Good Question 10 – The Cone Problem

From One Side or the Other.

MPAC 6 Communicating

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this: