Tag Archives: solid of revolution

Why Applications?

Posted on by
Reply

I guess the obvious answer is so you will have something to use your new knowledge of the definite integral on. This unit is a collection of the first applications. There are many more.

The whole idea is based on the fact that a definite integral is a sum. Thus, they can be used to add things. Complicated shapes can be divided into simple shapes, like rectangles, and their areas can be added.

Here are the first uses.

AVERAGE VALUE OF A FUNCTION ON AN INTERVAL

You know that to average two numbers you add them and divide the total by two. To average a larger set of numbers you add them and divide the sum by the number of numbers. Now you will learn how to average the infinite number of y-values of a function over an interval. To do it you use a definite integral.

HINT: Average value of a function, average rate of change of a function, and the mean value theorem all sound kind of the same. Furthermore, the formulas all look kind of the same. Don’t mix them up. Use their full name, not just “average,” and use the right one.

There is an interesting result found some years ago by a tenth-grade student who took AB Calculus in eighth grade and BC in ninth. He proved that Most Triangles Are Obtuse! using the average value integral.

LINEAR MOTION

This application extends your previous work on objects moving on a line. By adding, with a definite integral, you will be able to determine how far the object moves in a given time. Knowing that and where the object starts, you will be able to find its current position. BC students will also learn how to find the length of a curve in the plane.

THE AREA BETWEEN TWO CURVES

This application extends what you know about finding the area between a curve and the x-axis to finding the area between two curves.

VOLUME OF A SOLID FIGURE WITH A REGULAR CROSS-SECTION

Some solid objects, when sliced in the right way, have regular cross-section. That means, the cut surface is a square, a rectangle, a right triangle, a semi-circle and so on. Think of cutting a piece of butter from a stick of butter – each piece is a square with a little thickness, like a very small pizza box. By using an integral to add their volumes you can find the volume of the original figure. .

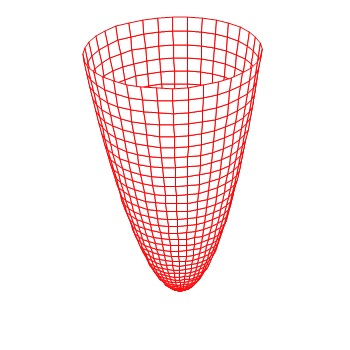
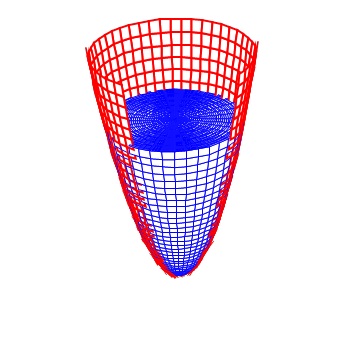
VOLUME OF A SOLID OF REVOLUTION – DISK METHOD

A region in the plane is revolved aroud a line resulting in a solid figure. Finding its volume is just a special case of a solid with regular cross section where the cross section is a circle. Each little piece is a disk. By adding their volumes with an integral you can calculate the volume.

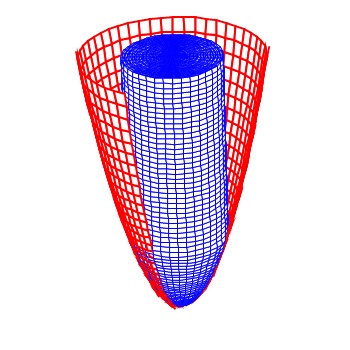
VOLUME OF A SOLID OF REVOLUTION – WASHER METHOD

Some solids of revolution have holes through them. These are formed by revolving a plane figure (usually the region between two curves) around an edge or a line outside the figure. The line is often the x– or y-axis. There is a formula for doing this, but understanding what you are doing – doing two disk problems – will help you with doing this. (See Subtract the Hole from the Whole.)

One last hint: You will want to know what the solid figure looks like. In addition to the illustrations in your textbook, there are various places online where you can find pictures of the figures. You can build models of them. There is an excellent iPad app called A Little Calculus that does a good job of illustrating and animating solid figures (and lots of other calculus stuff).

Course and Exam Description Unit 8

Area and Volume Problems (Type 4)

Posted on by
2

AP Type Questions 4: Area and Volume

Given equations that define a region in the plane students are asked to find its area, the volume of the solid formed when the region is revolved around a line, and/or the region is used as a base of a solid with regular cross-sections. This standard application of the integral has appeared every year since year one (1969) on the AB exam and almost every year on the BC exam. You can be fairly sure that if a free-response question on areas and volumes does not appear, the topic will be tested on the multiple-choice section.

What students should be able to do:

  • Find the intersection(s) of the graphs and use them as limits of integration (calculator equation solving). Write the equation followed by the solution; showing work is not required. Usually, no credit is earned until the solution is used in context (e.g., as a limit of integration). Students should know how to store and recall these values to save time and avoid copy errors.
  • Find the area of the region between the graph and the x-axis or between two graphs.
  • Find the volume when the region is revolved around a line, not necessarily an axis or an edge of the region, by the disk/washer method. See “Subtract the Hole from the Whole”
  • The cylindrical shell method will never be necessary for a question on the AP exams but is eligible for full credit if properly used.
  • Find the volume of a solid with regular cross-sections whose base is the region between the curves. For an interesting variation on this idea see 2009 AB 4(b)
  • Find the equation of a vertical line that divides the region in half (area or volume). This involves setting up an integral equation where the limit is the variable for which the equation is solved.
  • For BC only – find the area of a region bounded by polar curves: \displaystyle A=\frac{1}{2}{{\int_{{{{\theta }_{1}}}}^{{{{\theta }_{2}}}}{{\left( {r\left( \theta \right)} \right)}}}^{2}}d\theta
  • For BC only – Find perimeter using arc length integral

If this question appears on the calculator active section, it is expected that the definite integrals will be evaluated on a calculator. Students should write the definite integral with limits on their paper and put its value after it. It is not required to give the antiderivative and if a student gives an incorrect antiderivative, they will lose credit even if the final answer is (somehow) correct.

There is a calculator program available that will give the set-up and not just the answer so recently this question has been on the no calculator allowed section. (The good news is that in this case the integrals will be easy, or they will be set-up-but-do-not-integrate questions.)

Occasionally, other type questions have been included as a part of this question. See 2016 AB5/BC5 which included an average value question and a related rate question along with finding the volume.

Shorter questions on this concept appear in the multiple-choice sections. As always, look over as many questions of this kind from past exams as you can find.

For some previous posts on this subject see January 9, 11, 2013 and “Subtract the Hole from the Whole” of December 6, 2016.

The Area and Volume question covers topics from Unit 6 of the CED .

Free-response questions:

  • Variations: 2009 AB 4, Don’t overlook this one, especially part (b)
  • 2016 AB5/BC5,
  • 2017 AB 1 (using a table),
  • 2018 AB 5 – average rate of change, L’Hospital’s Rule
  • 2019 AB 5
  • Perimeter parametric curves 2011 BC 3 and 2014 BC 5
  • Area in polar form 2017 BC 5, 2018 BC 5, 20129 BC 2
  • 2021 AB 3/ BC 3
  • 2022 AB2 – area, volume, inc/dec analysis, and related rate.
  • 2023 BC 5 – Area, Improper integral, Integration by Parts (No area problem on 2023 AB exam)

Multiple-choice questions from non-secure exams:

  • 2008 AB 83 (Use absolute value),
  • 2012 AB 10, 92
  • 2012 BC 87, 92 (Polar area)

Updated March 12, 2012, March 22, 2022, May 4, 2023, June 4, 2023

…but what does it look like?

Posted on by
1

It will soon be time to teach about finding the volumes of solid figures using integration techniques. Here is a list of links to posts that will help your students what these figures look like and how they are generated.

Visualizing Solid Figures 1 Here are ideas for making physical models of solid figures. These make good projects for students.

A Little Calculus is an iPad app that does an excellent job in helping students visualize many of the concepts of the calculus. Volumes with regular cross section, disk method, washer method, cylindrical shells are all illustrated.

The first illustrations show square cross sections on a semicircular base. The base is in the lower part and the solid in the upper. By using the plus and minus button (lower right) you can increase or decrease the number of sections in real time and see the figures change. The upper figure may be rotated by moving your finger on the screen.

The illustration below shows a washer situation.

The following older posts show how to use Winplot to generate and explore solid figures. Unfortunately, Winplot seems to have gone out of favor. I’m not sure why; it is one of the best. I still use it and like it. You may download Winplot here for free (PC only).

Visualizing Solid Figures 2 This post demonstrates how to use Winplot to generate solids with regular cross sections and solids of rotation.

Visualizing Solid Figures 3 The washer method is illustrated using Winplot. These post all relate to finding volumes by washers: Subtract the Hole from the Whole and Does Simplifying Make Things Simpler?

Visualizing Solid Figures 4 Using Winplot to see the method cylindrical shells. Note that this method is not tested on either the AB or BC Calculus exams, so you do not have to teach it. Many teachers present this topic after the exams are given. As a footnote you may also find Why You Never Need Cylindrical Shells interesting. (However, this is not the reason it is not tested on the AP Calculus exams.)

Visualizing Solid Figures 5 An exercise demonstrating how “half” can mean different things and shows that how the figures are generated makes a difference.

Area and Volume Problems (Type 4)

Posted on by
3

AP Type Questions 4: Area and Volume

Given equations that define a region in the plane students are asked to find its area, the volume of the solid formed when the region is revolved around a line, and/or the region is used as a base of a solid with regular cross-sections. This standard application of the integral has appeared every year since year one (1969) on the AB exam and almost every year on the BC exam. You can be pretty sure that if a free-response question on areas and volumes does not appear, the topic will be tested on the multiple-choice section.

What students should be able to do:

  • Find the intersection(s) of the graphs and use them as limits of integration (calculator equation solving). Write the equation followed by the solution; showing work is not required. Usually no credit is earned until the solution is used in context (as a limit of integration). Students should know how to store and recall these values to save time and avoid copy errors.
  • Find the area of the region between the graph and the x-axis or between two graphs.
  • Find the volume when the region is revolved around a line, not necessarily an axis or an edge of the region, by the disk/washer method. See “Subtract the Hole from the Whole”
  • The cylindrical shell method will never be necessary for a question on the AP exams, but is eligible for full credit if properly used.
  • Find the volume of a solid with regular cross-sections whose base is the region between the curves. For an interesting variation on this idea see 2009 AB 4(b)
  • Find the equation of a vertical line that divides the region in half (area or volume). This involves setting up an integral equation where the limit is the variable for which the equation is solved.
  • For BC only – find the area of a region bounded by polar curves: A=\tfrac{1}{2}\int\limits_{{{\theta }_{1}}}^{{{\theta }_{2}}}{{{\left( r\left( \theta  \right) \right)}^{2}}}d\theta
  • For BC only – Find perimeter using arc length integral

If this question appears on the calculator active section, it is expected that the definite integrals will be evaluated on a calculator. Students should write the definite integral with limits on their paper and put its value after it. It is not required to give the antiderivative and if a student gives an incorrect antiderivative they will lose credit even if the final answer is (somehow) correct.

There is a calculator program available that will give the set-up and not just the answer so recently this question has been on the no calculator allowed section. (The good news is that in this case the integrals will be easy or they will be set-up-but-do-not-integrate questions.)

Occasionally, other type questions have been included as a part of this question. See 2016 AB5/BC5 which included an average value question and a related rate question along with finding the volume.

Shorter questions on this concept appear in the multiple-choice sections. As always, look over as many questions of this kind from past exams as you can find.

For some previous posts on this subject see January 9, 11, 2013 and “Subtract the Hole from the Whole” of December 6, 2016.

The Area and Volume question covers topics from Unit 6 of the 2019 CED .

Free-response questions:

  • Variations: 2009 AB 4, Don’t overlook this one, especially part (b)
  • 2016 AB5/BC5,
  • 2017 AB 1 (using a table),
  • 2018 AB 5 – average rate of change, L’Hospital’s Rule
  • 2019 AB 5
  • Perimeter parametric curves 2011 BC 3 and 2014 BC 5
  • Area in polar form 2017 BC 5, 2018 BC 5, 20129 BC 2

Multiple-choice questions from non-secure exams:

  • 2008 AB 83 (Use absolute value),
  • 2012 AB 10, 92
  • 2012 BC 87, 92 (Polar area)

 

 

 

 

 

 

Revised March 12, 2012

 

2019 CED Unit 8: Applications of Integration

Posted on by
Reply

This unit seems to fit more logically after the opening unit on integration (Unit 6). The Course and Exam Description (CED) places Unit 7 Differential Equations before Unit 8 probably because the previous unit ended with techniques of antidifferentiation. My guess is that many teachers will teach Unit 8: Applications of Integration immediately after Unit 6 and before Unit 7: Differential Equations. The order is up to you. 

Unit 8 includes some standard problems solvable by integration (CED – 2019 p. 143 – 161). These topics account for about 10 – 15% of questions on the AB exam and 6 – 9% of the BC questions.

Topics 8.1 – 8.3 Average Value and Accumulation

Topic 8.1 Finding the Average Value of a Function on an Interval Be sure to distinguish between average value of a function on an interval, average rate of change on an interval and the mean value

Topic 8.2 Connecting Position, Velocity, and Acceleration of Functions using Integrals Distinguish between displacement (= integral of velocity) and total distance traveled (= integral of speed)

Topic 8. 3 Using Accumulation Functions and Definite Integrals in Applied Contexts The integral of a rate of change equals the net amount of change. A really big idea and one that is tested on all the exams. So, if you are asked for an amount, look around for a rate to integrate.

Topics 8.4 – 8.6 Area

Topic 8.4 Finding the Area Between Curves Expressed as Functions of x

Topic 8.5 Finding the Area Between Curves Expressed as Functions of y

Topic 8.6 Finding the Area Between Curves That Intersect at More Than Two Points Use two or more integrals or integrate the absolute value of the difference of the two functions. The latter is especially useful when do the computation of a graphing calculator.

Topics 8.7 – 8.12 Volume

Topic 8.7 Volumes with Cross Sections: Squares and Rectangles

Topic 8.8 Volumes with Cross Sections: Triangles and Semicircles

Topic 8.9 Volume with Disk Method: Revolving around the x– or y-Axis Volumes of revolution are volumes with circular cross sections, so this continues the previous two topics.

Topic 8.10 Volume with Disk Method: Revolving Around Other Axes

Topic 8.11 Volume with Washer Method: Revolving Around the x– or y-Axis See Subtract the Hole from the Whole for an easier way to remember how to do these problems.

Topic 8.12 Volume with Washer Method: Revolving Around Other Axes. See Subtract the Hole from the Whole for an easier way to remember how to do these problems.

Topic 8.13  Arc Length BC Only

Topic 8.13 The Arc Length of a Smooth, Planar Curve and Distance Traveled  BC ONLY

Timing

The suggested time for Unit 8 is  19 – 20 classes for AB and 13 – 14 for BC of 40 – 50-minute class periods, this includes time for testing etc.

Previous posts on these topics for both AB and BC include:

Average Value and Accumulation

Average Value of a Function and Average Value of a Function

Half-full or Half-empty

Accumulation: Need an Amount?

AP Accumulation Questions

Good Question 7 – 2009 AB 3 Accumulation, explain the meaning of an integral in context, unit analysis

Good Question 8 – or Not Unit analysis

Graphing with Accumulation 1 Seeing increasing and decreasing through integration

Graphing with Accumulation 2 Seeing concavity through integration

Area

Area Between Curves

Under is a Long Way Down  Avoiding “negative area.”

Improper Integrals and Proper Areas  BC Topic

Math vs. the “Real World”  Improper integrals  BC Topic

Volume

Volumes of Solids with Regular Cross-sections

Volumes of Revolution

Why You Never Need Cylindrical Shells

Visualizing Solid Figures 1

Visualizing Solid Figures 2

Visualizing Solid Figures 3

Visualizing Solid Figures 4

Visualizing Solid Figures 5

Painting a Point

Subtract the Hole from the Whole and Does Simplifying Make Things Simpler?

Other Applications of Integrals

Density Functions have been tested in the past, but are not specifically listed on the CED then or now.

Who’d a Thunk It? Some integration problems suitable for graphing calculator solution

Here are links to the full list of posts discussing the ten units in the 2019 Course and Exam Description.

2019 CED – Unit 1: Limits and Continuity

2019 CED – Unit 2: Differentiation: Definition and Fundamental Properties.

2019 CED – Unit 3: Differentiation: Composite , Implicit, and Inverse Functions

2019 CED – Unit 4 Contextual Applications of the Derivative  Consider teaching Unit 5 before Unit 4

2019 – CED Unit 5 Analytical Applications of Differentiation  Consider teaching Unit 5 before Unit 4

2019 – CED Unit 6 Integration and Accumulation of Change

2019 – CED Unit 7 Differential Equations  Consider teaching after Unit 8

2019 – CED Unit 8 Applications of Integration   Consider teaching after Unit 6, before Unit 7

2019 – CED Unit 9 Parametric Equations, Polar Coordinates, and Vector-Values Functions 

2019 CED Unit 10 Infinite Sequences and Series

 

 

 

 

 

 

Applications of integrals, part 2: Volume problems

Posted on by
Reply

One of the major applications of integration is to find the volumes of various solid figures.

Volume of Solids with Regular Cross-sections  This is where to start with volume problems. After all, solids of revolution are just a special case of solids with regular cross-sections.

Volumes of Revolution

Subtract the Hole from the Whole and Does Simplifying Make Things Simpler?

Visualizing Solid Figures

Area and Volume (Type 4)  also Area and Volume Question review notes.

Why you Never Need Cylindrical Shells

Painting a Point

 

 

 

 

 

Visualizing Solid Figures 5

Posted on by
Reply

To end this series of posts on visualizing solid figures, we will look at a problem that relates to how volumes of solid figures are formed. It has 5 parts which will be presented first. Then the solution will be given.

Consider the region in the first quadrant bounded by the graphs of the parabola y={{x}^{2}} and the line y=9 both for 0\le x\le 3.

half A

This region is revolved around the y-axis to form a solid figure.

half B

  1. Use the disk/washer method to find the volume of this figure.
  2. Use the method of cylindrical shells to find the volume of this figure.
  3. Use the disk/washer method to find a number j , such that when x = j the volume of the figure is one-half that of the original figure.
  4. Use the method of cylindrical shells to find a number k , such that when x = k the volume of the figure is one-half that of the original figure.
  5. The answers to parts a) and b) should be the same, but the answers to parts c) and d) are different. Explain why they are different.

 

Solutions:

1. The volume by the disk/washer method is

\displaystyle V=\int_{0}^{9}{\pi {{x}^{2}}dy}=\int_{0}^{9}{\pi ydy}=\frac{81}{2}\pi \approx 127.235

     2. The volume by the method of cylindrical shells is

\displaystyle \int_{0}^{3}{2\pi x\left( 9-y \right)dx}=\int_{0}^{3}{2\pi x\left( 9-{{x}^{2}} \right)dx}=\frac{81}{2}\pi \approx 127.235

     3. The value is be found by solving the equation for j:

\displaystyle \int_{0}^{{{j}^{2}}}{\pi y\,dy}=\frac{81}{4}\pi , so j\approx 2.52269

     4. The value is be found by solving the equation for k:

\displaystyle \int_{0}^{k}{2\pi x\left( 9-{{x}^{2}} \right)dx}=\frac{81}{4}\pi  and k\approx 1.62359

     5. The reason the values are not the same is this. Think of the revolved parabola as a bowl. If you pour water into the bowl until it is half full, the bowl looks like the figure below. The water is pooled in the bottom of the bowl as you would expect. This is what happens when using the disk/washer method. The washers stack up starting in the bottom of the bowl until it is half full.

half C

On the other hand, the method of cylindrical shells sort of wraps the water in layers (the shells) around the y-axis. Picture the water being sprayed on the y-axes and frozen there. Each new layer (shell) increases the amount and you end up half of the total volume arranged as a cylinder with a rounded (paraboloid shaped) bottom as shown in the figure below. Both bowls contain the same amount of water, arranged differently.

Half D