Tag Archives: area

Who’d a thunk it?

Posted on by
Reply

Cubic Symmetry

Some things are fairly obvious. For example, if you look at the graphs of a few cubic equations, you might think that each is symmetric to a point and on closer inspection the point of symmetry is the point of inflection.

This is true and easy to prove. You can find the point of inflection, and then show that any point a certain distance horizontally on one side is the same distance above (or below) the point of inflection as a point the same distance horizontally on the other side is below (or above). Another way is to translate the cubic so that the point of inflection is at the origin and then show the resulting function is an odd function (i.e. symmetric to the origin).

But some other properties are not at all obvious. How someone thought to look for them is not even clear.

Tangent Line.

If you have cubic function with real roots of x = a, x = b, and x = c not necessarily distinct, if you draw a tangent line at a point where x is the average of any two roots, x = ½(a + b), , then this tangent line intersects the cubic on the x-axis at exactly the third root, x = c. Here is a Desmos graph illustrating this idea.

Here is a proof done with a CAS. The first line is a cubic expressed in terms of its roots.  The third line asks where the tangent line at x = m intersects the x-axis. The last line is the answer: x = c or whenever a = b (i.e. when the two roots are the same, in which case the tangent line is the x-axis and of course also contains x = c.

Areas
Even harder to believe is this: Draw a tangent line anywhere on a cubic. This tangent will intersect the cubic at a second point and the line and the cubic will define a region whose area is A1. From the second point draw a tangent what intersects the cubic at a third point and defines a region whose area is A2. The ratio of the areas A2/A1 = 16. I have no idea why this should be so, but it is.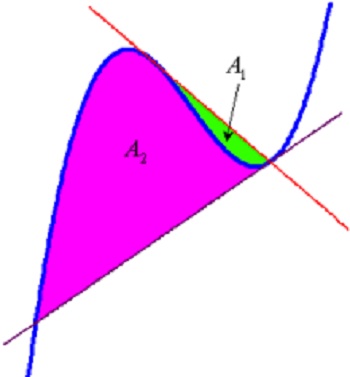

Here is a proof, again by CAS: The last line marked with a square bullet is the computation of the ratio and the answer, 16, is in the lower right,

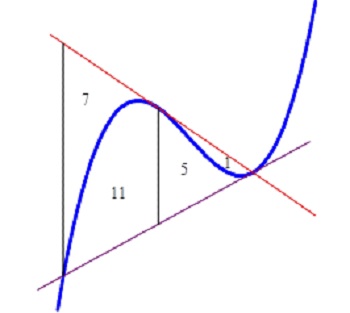
And if that’s not strange enough, inserting two vertical lines defines other regions whose areas are in the ratios shown in the figure below.

Who’d a thunk it?

.

Area & Volume (Type 4)

Posted on by
1

Given equations that define a region in the plane students are asked to find its area and the volume of the solid formed when the region is revolved around a line or used as a base of a solid with regular cross-sections. This standard application of the integral has appeared every year since 1969 on the AB exam and all but one year on the BC exam.

What students should be able to do:

  • Find the intersection(s) of the graphs and use them as limits of integration (calculator equation solving). Write the equation followed by the solution; showing work is not required. Usually no credit is earned until the solution is used in context (as a limit of integration). Students should know how to store and recall these values to save time and avoid copy errors.
  • Find the area of the region between the graph and the x-axis or between two graphs.
  • Find the volume when the region is revolved around a line, not necessarily an axis or an edge of the region, by the disk/washer method.
  • The cylindrical shell method will never be necessary for a question on the AP exams, but is eligible for full credit if properly used.
  • Find the volume of a solid with regular cross-sections whose base is the region between the curves. For an interesting variation on this idea see 2009 AB 4(b)
  • Find the equation of a vertical line that divides the region in half (area or volume). This involves setting up and solving an integral equation where the limit is the variable for which the equation is solved.
  • For BC only – find the area of a region bounded by polar curves: A=\tfrac{1}{2}\int\limits_{{{\theta }_{1}}}^{{{\theta }_{2}}}{{{\left( r\left( \theta  \right) \right)}^{2}}}d\theta

If this question appears on the calculator active section, it is expected that the definite integrals will be evaluated on a calculator. Students should write the definite integral with limits on their paper and put its value after it.  It is not required to give the antiderivative and if a student gives an incorrect antiderivative they will lose credit even if the final answer is (somehow) correct.

There is a calculator program available that will give the set-up and not just the answer so recently this question has been on the no calculator allowed section. (The good news is that in this case the integrals will be easy or they will be set-up-but-do-not-integrate questions.)

Occasionally, other type questions have been included as a part of this question. See 2016 AB5/BC5 which included an average value question and a related rate question along with finding the volume.

Shorter questions on this concept appear in the multiple-choice sections. As always, look over as many questions of this kind from past exams as you can find.

For some previous posts on this subject see January 9, 11, 2013

Next Posts:

Friday March 17: Table and Riemann sums (Type 5)

Tuesday Match 21: Differential Equations (Type 6)

Friday March 24: Others (Type 7: related rates, implicit differentiation, etc.)

Tuesday March 28: for BC Parametric Equation (Type 8)

Variations on a Theme by ETS

Posted on by
1

Experienced AP calculus teacher use as many released exam questions during the year as they can. They are good questions and using them gets the students used to the AP style and format.  They can be used “as is”, but many are so rich that they can be tweaked to test other concepts and to make the students think wider and deeper.  

Below is a multiple-choice question from the 2008 AB calculus exam, question 9.

 2008 mc9The graph of the piecewise linear function f  is shown in the figure above. If \displaystyle g\left( x \right)=\int_{-2}^{x}{f\left( t \right)\,dt}, which of the following values is the greatest?

(A)  g(-3)         (B)  g(-2)         (C)  g(0)         (D)  g(1)         (E)  g(2)

I am now going to suggest some ways to tweak this question to bring out other ideas. Here are my suggestions. Some could be multiple-choice others simple short constructed response questions. A few of these questions, such as 3 and 4, ask the same thing in different ways.

      1. Require students to show work or justify their answer even on multiple-choice questions. So for this question they should write, “The answer is (D) g(1) since x = 1 is the only place where {g}'\left( x \right)=f\left( x \right) changes from positive to negative.” 
      2. Ask, “Which of the following values is the least?” (Same choices)
      3. Find the five values listed.
      4. Put the five values in order from smallest to largest.
      5. If \displaystyle g\left( x \right)=g\left( -2 \right)+\int_{-2}^{x}{f\left( t \right)dt} and the maximum value of g is 7, what is the minimum value?
      6. If \displaystyle g\left( x \right)=g\left( -2 \right)+\int_{-2}^{x}{f\left( t \right)dt} and the minimum value of g is 7, what is the maximum value?
      7. Pick any number (not just an integers) in the interval [–3, 2] to be a and change the stem to read, “If \displaystyle g\left( x \right)=g\left( a \right)+\int_{a}^{x}{f\left( t \right)dt} ….” And then ask any of the questions above – some answers will be different, some will be the same. Discussing which will not change and why makes a worthwhile discussion.
      8. Change the equation in the stem to \displaystyle g\left( x \right)=3x+\int_{-2}^{x}{f\left( t \right)dt} and ask the questions above. Again most of the answers will change. Also this question and the next start looking like some free-response questions. Compare them with 2011 AB 4 and 2010 AB 5(c)
      9. Change the equation in the stem to \displaystyle g\left( x \right)=-\tfrac{3}{2}x+\int_{-2}^{x}{f\left( t \right)dt} and ask the questions above. This time most of the answers will change.
      10. Change the graph and ask the same questions.

Not all questions offer as many variations as this one. For some about all you can do is use them “as is” or just change the numbers.

Any other adaptations you can think of?

What is your favorite question for tweaking?

 Math in the News Combinatorics and UPS

Revised: August 24, 2014

Area and Volume Questions

Posted on by
Reply

AP Type Questions 4

Given equations that define a region in the plane students are asked to find its area and the volume of the solid formed when the region is revolved around a line or used as a base of a solid with regular cross-sections. This standard application of the integral has appeared every year since 1969 on the AB exam and all but one year on the BC exam.

If this appears on the calculator active section, it is expected that the definite integrals will be evaluated on a calculator. Students should write the definite integral with limits on their paper and put its value after it.  It is not required to give the antiderivative and if students give an incorrect antiderivative they will lose credit even if the final answer is (somehow) correct.

There is a calculator program available that will give the set-up and not just the answer so recently this question has been on the no calculator allowed section. (The good news is that the integrals will be easy or they will be set-up but do not integrate questions.)

What students should be able to do:

  • Find the intersection(s) of the graphs and use them as limits of integration (calculator equation solving). Write the equation followed by the solution; showing work is not required. Usually no credit is earned until the solution is used in context (as a limit of integration).
  • Find the area of the region between the graph and the x-axis or between two graphs.
  • Find the volume when the region is revolved around a line, not necessarily an axis, by the disk/washer method. (Shell method is never necessary, but is eligible for full credit if properly used).
  • Find the volume of a solid with regular cross-sections whose base is the region between the curves. But see 2009 AB 4(b)
  • Find the equation of a vertical line that divides the region in half (area or volume). This involves setting up and solving an integral equation where the limit is the variable for which the equation is solved.
  • For BC only – find the area of a region bounded by polar curves:

\displaystyle A=\tfrac{1}{2}{{\int_{{{t}_{1}}}^{{{t}_{2}}}{\left( r\left( t \right) \right)}}^{2}}dt

Shorter questions on this concept appear in the multiple-choice sections. As always, look over as many questions of this kind from past exams as you can find.

For some previous posts on this subject see January 9, 11, 2013

Painting a Point

Posted on by
Reply

Accumulation 7: An application (of paint)

Suppose you started with a point, the origin to be specific, and painted it. You put on layers and layers of paint until your point grows to a sphere with radius r. Let’s stop and admire your work part way through the job; at this point the radius is {{x}_{i}} and 0\le {{x}_{i}}\le r.

How much paint will you need for the next layer?

Easy: you need an amount equal to the surface area of the sphere, 4\pi {{x}_{i}}^{2}, times the thickness of the paint. As everyone knows paint is thin, specifically \Delta x thin. So we add an amount of paint to the sphere equal to 4\pi {{x}^{2}}\left( \Delta x \right).

The volume of the final sphere must be the same as the total amount of paint. The total amount of paint must be the (Riemann) sum of all the layers or \displaystyle \sum\limits_{i=1}^{n}{4\pi {{x}_{i}}^{2}\left( \Delta x \right)}. As usual \Delta x is very thin, tending to zero as a matter of fact, so the amount of paint must be

\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\sum\limits_{i=1}^{n}{4\pi {{x}_{i}}^{2}\left( \Delta x \right)=\int_{0}^{r}{4\pi {{x}^{2}}}dx=\left. \tfrac{4}{3}\pi {{x}^{3}} \right|_{0}^{r}=\tfrac{4}{3}\pi {{r}^{3}}}.

A standard related rate problem is to show that the rate of change of the volume of a sphere is proportional to its surface area – the constant of proportionality is dr/dt. So it should not be a surprise that the integral of this rate of change of the surface area is the volume. The integral of a rate of change is the amount of change.

Interestingly this approach works other places as long as you properly define “radius:”

  • A circle centered at the origin with radius x and perimeter of 2\pi x, gains area at a rate equal to its perimeter times the “thickness of the edge” \Delta x: \displaystyle A=\underset{n\to \infty }{\mathop{\lim }}\,\sum\limits_{k=1}^{n}{2\pi x\Delta x}=\int_{0}^{r}{2\pi x\,dx=\pi {{r}^{2}}}
  • A square centered at the origin with “radius” x with sides whose length are s =2 x, gains area at a rate equal to its perimeter (8x) times the “thickness of the edge” \Delta x:  \displaystyle A=\underset{n\to \infty }{\mathop{\text{lim}}}\,\sum\limits_{k=1}^{n}{8x\Delta x=\int_{0}^{x}{8x\,dx}}=4{{x}^{2}}={{(2x)}^{2}}={{s}^{2}}
  • A cube centered at the origin with “radius” x and edges of length 2x, gains volume at a rate equal to its surface area, 6(4{{x}^{2}}), times the “thickness of the face” \Delta x – think paint again: V=\underset{n\to \infty }{\mathop{\text{lim}}}\,\sum\limits_{k=1}^{n}{\text{6(4}{{\text{x}}^{2}})\Delta x}=\int_{0}^{x}{24{{x}^{2}}dx}=8{{x}^{3}}={{(2x)}^{3}}={{s}^{3}}

Area Between Curves

Posted on by
1

Applications of Integration 1 – Area Between Curves

The first thing to keep in mind when teaching the applications of integration is Riemann sums. The thing is that when you set up and solve the majority of application problems you cannot help but develop a formula for the situation. Students think formulas are handy and go about memorizing them badly. By which I mean they forget or never learn where the various things in the formula come from. A slight change in the situation and they are lost. Behind every definite integral stands a Riemann sum; each application should be approached through its Riemann sum. If students understand that, they will make fewer mistakes with the “formula.”

As I suggested in a previous post, I believe all area problems should be treated as the area between two curves. If you build the Riemann sum rectangle between the graph and the axis and calculate its vertical side as the upper function minus the lower (or right minus left if you use horizontal rectangles) you will always get the correct integral for the area. If the upper curve is the x-axis, then the vertical sides of the Riemann sums are (0 – f(x)) and you get a positive area as you should.

If both your curves are above the x-axis, then it is tempting to explain what you are doing as subtracting the area between the lower curve and the x-axis from the area between the upper curve and the x-axis. And this is not wrong. It just does not work very smoothly when one, both or parts of either are below the x-axis. Then you go into all kinds of contortions explaining things in terms of positive and negative areas.  Why go there?

Regardless of where the two curves are relative to the x-axis, the vertical distance between them is the upper value minus the lower, f(x) – g(x). It does not matter if one or both functions are negative on all or part of the interval, the difference is positive and the area between them is

\displaystyle \underset{n\to \infty }{\mathop{\lim }}\,\sum\limits_{i=1}^{n}{\left( f\left( {{x}_{i}} \right)-g\left( {{x}_{i}} \right) \right)\Delta {{x}_{i}}}=\int_{a}^{b}{f\left( x \right)-g\left( x \right)dx}.

Furthermore, this Riemann sum rectangle is used in other applications. It is the one rotated in both the washer and shell method of finding volumes. So in area and all applications be sure your students don’t just memorize formulas, but keep their eyes on the rectangle and the Riemann sum.

Finally, if the graphs cross in the interval so that the upper and lower curves change place, you may (1) either break the problem into several pieces so that your integrands are always of the form upper minus lower, or (2) if you intend to do the computation using technology, set up the integral as

\displaystyle \int_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|dx}.

Under is a Long Way Down

Posted on by
1

The development of the ideas and concepts related to definite integrals almost always begins with finding the area of a region between a graph in the first quadrant and the x-axis between two vertical lines. Everyone, including me in the past, refers to this as “finding the area under the curve.”

Under is a long way down. And while everyone understands what this means, I suggest that a better phrasing is “finding the area between the curve and the x-axis.” Here is why:

  • That is what you are doing.
  • You will soon be finding the area between the curve and the x-axis where the curve is below the x-axis. This often leads to something you may be tempted to call “negative area” and of course there is no such thing as a negative area, regardless of what you may find in some textbooks.

As with so many integration problems, the results is often a formula that obscures what is really going on – the Riemann sum whose value the integral gives. The first such formula is that the area is given by \int_{a}^{b}{f\left( x \right)dx}. This is correct only if  f (x) > 0. There is a natural confusion for beginning students between the facts that if f (x) < 0 the integral comes out negative, but the area is positive.

For all the applications of integration always emphasize the Riemann sum – not just the final formula. In the area problem with f (x) > 0 the integrand is the vertical length of the rectangles that make up the sum and this is the upper function’s value minus the lower function’s value, with the lower being the x-axis, y = 0. Then when f (x) < 0 the upper minus the lower is 0 – f (x) and the area is given by \int_{a}^{b}{0-f\left( x \right)dx}=-\int_{a}^{b}{f\left( x \right)dx} which is positive as it should be. And students will immediately see that \int_{a}^{b}{f\left( x \right)dx} is not automatically the area.

To help students see this you could start (very first problem) by helping them to find the area of the region between f (x) > 0 and the line y = 1 so they have to deal with the lower curve. Then consider another problem using the x-axis.

There is a fair amount of ground to cover between the first area between the curve and the x-axis problems with f (x) > 0 and other area problems. Teaching students how to set up those first Riemann sums, what a Riemann sum is, the definition of the definite integral and even the Fundamental Theorem of Calculus may all come between the first problem and when this distinction becomes important. Starting with the right words, “area between the graph and the x-axis”, will help in the long run.