Implicit Differentiation of Parametric Equations

Posted on May 17, 2014 by Lin McMullin

I’ve never liked memorizing formulas. I would rather know where they came from or be able to tie it to something I already know. One of my least favorite formulas to remember and explain was the formula for the second derivative of a curve given in parametric form. No longer.

If $y=y\left( t \right)$ and, $x=x\left( t \right)$ then the tradition formula gives

$\displaystyle \frac{d}{dx}y\left( t \right)=\frac{dy/dt}{dx/dt}$ , and

$\displaystyle \frac{{{d}^{2}}y}{d{{x}^{2}}}=\frac{\frac{d}{dt}\left( \frac{dy}{dx} \right)}{\frac{dx}{dt}}$

It is that last part, where you divide by $\displaystyle \frac{dx}{dt}$ , that bothers me. Where did the $\displaystyle \frac{dx}{dt}$ come from?

Then it occurred to me that dividing by $\displaystyle \frac{dx}{dt}$ is the same as multiplying by $\displaystyle \frac{dt}{dx}$

It’s just implicit differentiation!

Since $\displaystyle \frac{dy}{dx}$ is a function of t you must begin by differentiating the first derivative with respect to t. Then treating this as a typical Chain Rule situation and multiplying by $\displaystyle \frac{dt}{dx}$ gives the second derivative. (There is a technical requirement here that given $x=x\left( t \right)$ , then $t={{x}^{-1}}\left( x \right)$ exists.)

In fact, if you look at a proof of the formula for the first derivative, that’s what happens there as well:

$\displaystyle \frac{d}{dx}y\left( t \right)=\frac{dy}{dt}\cdot \frac{dt}{dx}=\frac{dy/dt}{dx/dt}$

The reason you to do it this way is that since x is given as a function of t, it may be difficult to solve for t so you can find dt/dx in terms of x. But you don’t have to; just divide by dx/dt which you already know.

Here is an example for both derivatives.

Suppose that $x={{t}^{3}}-3$ and $y=\ln \left( t \right)$

Then $\displaystyle \frac{dy}{dt}=\frac{1}{t}$ , and $\displaystyle \frac{dx}{dt}=3{{t}^{2}}$ and $\displaystyle \frac{dt}{dx}=\frac{1}{3{{t}^{2}}}$ .

Then $\displaystyle \frac{dy}{dx}=\frac{1}{t}\cdot \frac{dt}{dx}=\frac{1}{t}\cdot \frac{1}{3{{t}^{2}}}=\frac{1}{3{{t}^{3}}}=\frac{1}{3}{{t}^{-3}}$

And $\displaystyle \frac{{{d}^{2}}y}{d{{x}^{2}}}=\left( \frac{d}{dt}\left( \frac{dy}{dx} \right) \right)\cdot \frac{dt}{dx}=\left( -{{t}^{-4}} \right)\cdot \frac{dt}{dx}=\left( -{{t}^{-4}} \right)\left( \frac{1}{3{{t}^{2}}} \right)=-\frac{1}{3{{t}^{6}}}$

Yes, it’s the same thing as using the traditional formula, but now I’ll never have to worry about forgetting the formula or being unsure how to explain why you do it this way.

Revised: Correction to last equation 5/18/2014

Revised: 2/8/2016

Mean Numbers

Posted on September 25, 2013 by Lin McMullin

Here is a problem for you and your students. The numbers are mean until you get to the end when they all become very nice and well-behaved.

You could give this to your students individually or as a group exploration. Give each person or group a different function and/or different intervals. Choose a function that has several (3 – 5) turning points in the interval. The function should be differentiable on the open interval and continuous on the closed interval.

It is intended that the work be done on a graphing calculator; you will need to carry 6 or 7 decimal places in their work.

Here is a typical problem. A link to the solution is given at the end.

Consider the function $f\left( x \right)=\sin \left( x \right)$ on the closed interval [1, 12].

Write an equation of a line, $y\left( x \right)$ , between the endpoints of the function. Give the decimal value of its slope and give a graph of the function and the line.
Write the equation of a function $h\left( x \right)$ that gives the vertical distance between $f\left( x \right)$ and $y\left( x \right)$ . Since f may be both above and below y this function may have positive and negative values.
Graph h and find its critical values. What are these places with respect to the graph of h?
Calculate the derivative of f at the critical values of h.
Interpret your result graphically.

Click here for the solution.

Foreshadowing the Chain Rule

Posted on September 20, 2013 by Lin McMullin

I assigned another very easy but good problem this week. It was simple enough, but it gave a hint of things to come.

Use the Product Rule to find the derivative of ${{\left( f\left( x \right) \right)}^{2}}$ .

Since we have not yet discussed the Chain Rule, the Product Rule was the only way to go.

$\frac{d}{dx}{{\left( f \right)}^{2}}=\frac{d}{dx}\left( f\cdot f \right)=f\cdot {f}'+{f}'\cdot f=2f\cdot f'$

And likewise for higher powers:

$\frac{d}{dx}{{f}^{3}}=\frac{d}{dx}\left( f\cdot f\cdot f \right)=f\cdot f\cdot {f}'+f\cdot {f}'\cdot f+{f}'\cdot f\cdot f=3{{f}^{2}}{f}'$

If you just look at the answer, it is not clear where the ${f}'$ comes from. But the result foreshadows the Chain Rule.

Then we used the new formula to differentiate a few expressions such as ${{\left( 4x+7 \right)}^{2}}$ and ${{\sin }^{2}}\left( x \right)$ and a few others.

Regarding the Chain Rule: I have always been a proponent of the Rule of Four, but I have never seen a good graphical explanation of the Chain Rule. (If someone has one, PLEASE send it to me – I’ll share it.)

Here is a rough verbal explanation that might help a little.

Consider the graph of $y=\sin \left( x \right)$ . On the interval $[0,2\pi ]$ it goes through all its value in order once – from 0 to 1 to 0 to -1 and back to zero. Now consider the graph of $y=\sin \left( 3x \right)$ . On the interval $\left[ 0,\tfrac{2\pi }{3} \right]$ it goes through all the same values in one-third of the time. Therefore, it must go through them three times as fast. So the rate of change of $y=\sin \left( 3x \right)$ between 0 and $\tfrac{2\pi }{3}$ must be three times the rate of change of $y=\sin \left( x \right)$ . So the rate of change of must be $3\cos \left( 3x \right)$ . Of course this rate of change is the slope and the derivative.

At Just the Right Time

Posted on September 12, 2013 by Lin McMullin

This is about a little problem that appeared at just the right time. My class had just learned about derivatives (limit definition) and the fact that the derivative is the slope of the tangent line. But none of that was really firm yet. I had assigned this problem for homework:¹

Find f (3) and f ‘ (3), assuming that the tangent line to y = f (x) at a = 3 has equation y = 5x + 2

To solve the problem, you need to realize that the tangent line and the function intersect at the point where x = 3. So, f (3) was the same as the point on the line where x = 3. Therefore, f (3) = 5(3) + 2 = 17.

Then you have to realize that the derivative is the slope of the tangent line, and we know the tangent line’s equation and we can read the slope. So f ‘ (3) = 5

In my previous retired years, I wrote a number of questions for several editions of a popular AP Calculus exam review book.² I found it easy to write difficult questions. But what I was after was good easy questions; they are more difficult to write. One type of good easy question is one that links two concepts in a way that is not immediately obvious such as the question above. I am always amazed at the good easy questions on the AP calculus exams. Of course, they do not look easy, but that’s what makes them good.

Now a month from now this question will not be a difficult at all – in fact it did not stump all of my students this week. Nevertheless, appearing at just the right time, I think it did help those it did stump, and that’s why I like it.

______________________

² These review books are published by D&S Marketing Systems, Inc. Website

More Gold

Posted on July 17, 2013 by Lin McMullin

Last week I discussed Lin McMullin’s Theorem (that would be me). The theorem finds where the Golden Ratio shows up in any fourth-degree polynomial. Shortly after that began making the rounds, I got an e-mail from David Tschappat who was then a senior in college. He is now a doctoral student working for an online learning solutions provider.

He related the discovery of a similar appearance of the Golden Ratio in cubic polynomials! Here is his theorem and two other related facts about cubic polynomials (lemmas really) as developed by me.

All cubic polynomials are symmetric to their point of inflection. Therefore, we can simplify matters by translating any cubic so that its point of inflection is at the origin. The general equation will then be $f\left( x \right)=k{{x}^{3}}-3{{h}^{2}}kx$ .

I choose this rather unusual form so that the x-coordinates of the extreme points will be “nice” variables, namely h and –h the zeros of ${f}'\left( x \right)=3k{{x}^{2}}-3{{h}^{2}}k=3k\left( x-h)(x+h \right)$ . The leading coefficient k will eventually divide out and not be a concern.

Now consider two other values x = –2h and x = 2h. So, assuming h > 0, there are five evenly spaced values $-2h<-h<0<h<2h$ that we will consider.

The first two results I will leave as an exercise, as they say:

$f\left( -2h \right)=f\left( h \right)$ and $f\left( -h \right)=f\left( 2h \right)$ . This means that the extreme values are the same as a point on the graph 3h units away on the other side of the y-axis. This is mildly interesting in itself. The reason it is mentioned id that we will use these points soon.
${f}'\left( -2h \right)={f}'\left( 2h \right)$ which is really true for any points at equal distances on opposite sides of the origin. This is obvious from the symmetry of the cubic.

Now comes the interesting and strange part. An equation of a line through one extreme point with a slope equal to that at the point with the same y-coordinate on the other side of the origin (or for that matter the point h units farther away on the same side of the y-axis) is

$y=f\left( -h \right)+{f}'\left( 2h \right)\left( x-\left( -h \right) \right)$

$y=\left( k{{\left( -h \right)}^{3}}-3{{h}^{2}}k\left( -h \right) \right)+\left( 3k{{\left( 2h \right)}^{2}}-3{{h}^{2}}k \right)\left( x+h \right)$

$y=k\left( 11{{h}^{3}}+9{{h}^{2}}x \right)$

Now find where this line intersect the original cubic by solving $y=f\left( x \right)$ . The equation can be solved by hand. We know that x = h is one solution. Synthetic division will give a quadratic and the quadratic formula will do the rest.

$k\left( 11{{h}^{3}}+9{{h}^{2}}x \right)=k{{x}^{3}}-3{{h}^{2}}kx$

$0={{x}^{3}}-12{{h}^{2}}x-11{{h}^{3}}$

$0=\left( x-h \right)\left( {{x}^{2}}+hx-11{{h}^{2}} \right)$

$\displaystyle x=h,\frac{1+3\sqrt{5}}{2}h,\frac{1-3\sqrt{5}}{2}h$

What? You were expecting the Golden Ratio? Not to worry; it’s there!

$\displaystyle \Phi \left( -h \right)+\phi \left( 2h \right)=\frac{1+\sqrt{5}}{2}\left( -h \right)+\frac{1-\sqrt{5}}{2}\left( 2h \right)=\frac{1-3\sqrt{5}}{2}h$

$\displaystyle \Phi \left( 2h \right)+\phi \left( -h \right)=\frac{1+\sqrt{5}}{2}\left( 2h \right)+\frac{1-\sqrt{5}}{2}\left( -h \right)=\frac{1+3\sqrt{5}}{2}h$

Where $\displaystyle \Phi =\frac{1+\sqrt{5}}{2}$ is the Golden Ratio and $\displaystyle \phi ={{\Phi }^{-1}}=\frac{1-\sqrt{5}}{2}$ is the reciprocal of the Golden Ratio.

A similar computation using the other extreme point gives similar results.

Yes, the Golden Ratio is there; I don’t know why it should be there, but it is.

Thank you, David.

Lin McMullin’s Theorem

Posted on July 10, 2013 by Lin McMullin

Mathematics more often tends to delight when it exhibits an unanticipated result rather than conforming to … expectations. In addition, the pleasure derived from mathematics is related in many cases to the surprise felt upon the perception of totally unexpected relationships and unities.

– Mario Livio, The Golden Ratio

I have a theorem named after me. I did not name it, but I did prove it – well more like I tripped over it. It is a calculus related idea. Here is how it came about. I say “came about” because as you will see I did not set out to prove it. I just sort of fell in my lap as I was working on something else.

I was trying to do an animation of an idea that I had heard about: If you have a fourth degree, or quartic, polynomial with a “W” shape it has two points of inflection. If you draw a line through the points of inflection three regions enclosed by the line and the polynomial’s graph are formed. The areas of these regions are in the ratio of 1:2:1. In order to make the animation work I needed the general coordinates of the four points where the line intersects the quartic.

The straightforward way to proceed would be to write a general fourth degree polynomial,

$f\left( x \right)={{c}_{4}}{{x}^{4}}+{{c}_{3}}{{x}^{3}}+{{c}_{2}}{{x}^{2}}+{{c}_{1}}x+{{c}_{0}}$

differentiate it twice to find the second derivative. Then find the zeros of the second derivative (by the quadratic formula), write the equation of the line through them, and then find where else the line intersects the quartic. Without even starting I realized that even with a CAS the algebra and equation solving was going to be really fun (Not!). So, I decided on an alternative approach.

I decided to let the zeros of the second derivative be x = a and x = b, then at least they would be easy to work with. Then the second derivative is 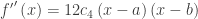$\displaystyle {{f}'}'\left( x \right)=12{{c}_{4}}\left( x-a \right)\left( x-b \right)$ where the 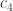${{c}_{4}}$ is the leading coefficient of the quartic and the 12 comes from differentiating twice.

I integrated to get the first derivative and added ${{c}_{1}}$ , the coefficient of the linear term, as the constant of integration. I integrated again and added ${{c}_{0}}$ , the constant term. as the constant of integration. This resulted in the original quartic function:

$\displaystyle f\left( x \right)={{c}_{4}}{{x}^{4}}-2\left( a+b \right){{c}_{4}}{{x}^{3}}+6ab{{c}_{4}}{{x}^{2}}+{{c}_{1}}x+{{c}_{0}}$

Then I wrote the equation of y(x) the line through the points of inflection. It is too long to copy, but you may see it in the screen capture at the end of the post. (That is what is nice about a CAS: you really do not have to worry about how complicated things are.)

Then I solved the equation $f\left( x \right)=y\left( x \right)$ . Two of the solutions are x = a and x = b as I expected. (This means that you could do synthetic division by hand since you know two of the roots.) The other two I did not expect. They are:

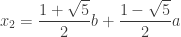
$\displaystyle {{x}_{1}}=\frac{1+\sqrt{5}}{2}a+\frac{1-\sqrt{5}}{2}b$ and $\displaystyle {{x}_{2}}=\frac{1+\sqrt{5}}{2}b+\frac{1-\sqrt{5}}{2}a$

And that’s when I stopped astonished! Those numbers are the Golden Ratio 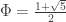$\Phi =\frac{1+\sqrt{5}}{2}$ , and its reciprocal $\phi ={{\Phi }^{-1}}=\frac{1-\sqrt{5}}{2}$ . So the roots are $\Phi a+\phi b$ and $\Phi b+\phi a$ . How did they get there?

To this day I have no idea why the Golden Ratio should be so involved with quartic polynomials, but there they are in every quartic!

There were no assumptions made about a and b – they could be Complex numbers. In that case there are no points of inflection, but the “line” and the quartic still will have the same value at the four points.

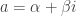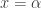
October 16, 2022 Update: If the solutions of $\displaystyle {y}''=0$ are the Complex conjugates $\displaystyle a=\alpha +\beta i$ and $\displaystyle b=\alpha -\beta i$ then $\displaystyle {{x}_{1}}=\alpha +\sqrt{5}\beta i$ and $\displaystyle {{x}_{2}}=\alpha -\sqrt{5}\beta i$ . When graphed on an Argand diagram the four points are collinear on the vertical line at $\displaystyle x=\alpha$

This was all in 2013 and until just this year I never checked the ratio of the areas. (They check.)

Here is a CAS printout of the entire computation.

An interactive Desmos demo of this can be found here

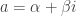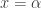
October 16, 2022, Update: If the solutions of $\displaystyle {y}''=0$ are the Complex conjugates $\displaystyle a=\alpha +\beta i$ and $\displaystyle b=\alpha -\beta i$ then $\displaystyle {{x}_{1}}=\alpha +\sqrt{5}\beta i$ and $\displaystyle {{x}_{2}}=\alpha -\sqrt{5}\beta i$ . When graphed on an Argand diagram the four points are collinear on the vertical line at $\displaystyle x=\alpha$

November 10, 2020, Update: I received an email this week form Dominique Laurain, a computer science and applied math engineer from France, who describes himself as a mathematics hobbyist. He discovered another interesting relationship between the coordinates of the x-coordinates of the four points on the line described above. The four points on the line through the points of inflection of a fourth degree polynomial with Real roots in the drawing above from left to right are p, q, r, and s. The coordinates of the points of inflection are a and b as in the post above.

One, of several, cross-ratios of four points with x-coordinates of p, q r, and s is defined as

$\displaystyle (p,s;r,q)=\frac{{\left( {r-p} \right)\left( {q-s} \right)}}{{\left( {r-s} \right)\left( {q-p} \right)}}$ .

Dominique Laurin discovered that 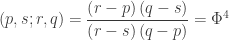$\displaystyle (p,s;r,q)=\frac{{\left( {r-p} \right)\left( {q-s} \right)}}{{\left( {r-s} \right)\left( {q-p} \right)}}={{\Phi }^{4}}$

The computation is shown in the figure below.

There are 24 other cross-ratios depending on the order of the points. In groups of 4, the 24 possible orders are equal to 6 related values. See the cross-ratio link above above. For example, the cross-ratio in the order (s, p; r, q) is 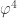${{\varphi }^{4}}$

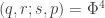
Also, $(q,r;s,p)={{\Phi }^{4}}$

Other interesting information:

The Golden Ratio also appears in cubic equations. See the Tashappat – McMullin theorem here.

“Quartic Polynomials and the Golden Ratio” by Harald Totland of the Royal Norwegian Naval Academy. (June 2009)

Speaking of the Golden Ratio, the Calculus Humor website has a nice feature on the Golden Ratio in logos. To view it click here.

Link for cross-ratios

Revised and updated July 20 and 23, 2017, November 10, 2020

Experimenting with CAS – Chain Rule

Posted on July 3, 2013 by Lin McMullin

Discovering things in mathematics can be facilitated by using a computer algebra system (CAS) available on many handheld calculators and computer apps. A CAS can provide good data with which to draw conclusions. You can do “experiments” by producing the results with a CAS and looking for patterns. As an example, let’s look at how you and your students might discover the chain rule for derivatives.

One of the ways you could introduce the chain rule is to ask your class to differentiate something like (3x + 7)². Not knowing about the chain rule, just about the only way to proceed is to expand the expression to 9x² + 42x + 49 and differentiate that: 18x + 42 and then factor 6(3x + 7). Then you show how this relates to the power rule and where the “extra” factor of 3 comes from differentiating the (3x + 7). You really cannot a much more complicated example, say a third or fourth power, because the algebra gets complicated very fast.

Or does it?

Suggest your students use a CAS to do the example above this time using the third power. The output might look like this:

But even better: what we want is just the answer. Who cares about all the algebra in between? Try a few powers until the pattern become obvious.

Now we have some good data to work with. Can you guess the pattern?

Nor sure where the “extra” factor of 3 comes from? Try changing the 3 in the original and keep the exponent the same.

Now can you guess the chain rule? See if what you thought is right by changing only the inside exponent.

Then you can try some others:

CAS D

You can count on the CAS giving you the correct data (answers). Do enough experiments until the chain rule pattern becomes clear.

But I think the big thing is not the chain rule, but that the students are learning how to experiment in mathematics situations. In these we started by changing only the outside power. Then we kept the power the same power and changed the coefficient of the linear factor. Then we changed the power inside power, each time seeing if our tentative rule for differentiating composite function was correct and adjusting it if it was not. Finally we tried a variety of different expressions. You change things. Not big things but little things. You don’t jump from one trial to something very different, only something a little different.

You can do the same thing for the product rule, the quotient rule, maybe some integration rules and so on. You have accomplished your goal when the students can produce the data they need without your suggestions.

But be aware: sometimes this can lead to unexpected results. Does the pattern hold here?

Or here?

Hint: $\frac{7}{3.2}=2.1875$ and $3{{\left( 3.2 \right)}^{3}}=98.304$

Revised 8-25-17

Teaching Calculus

The pleasure lies not in discovering the truth, but in searching for it.

Category Archives: Derivatives

Implicit Differentiation of Parametric Equations

Mean Numbers

Foreshadowing the Chain Rule

At Just the Right Time

More Gold

Lin McMullin’s Theorem

Experimenting with CAS – Chain Rule

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this: