Graph Analysis (Type 3)

Posted on March 10, 2017 by Lin McMullin

The long name is “Here’s the graph of the derivative, tell me things about the function.”

Most often students are given the graph identified as the derivative of a function. There is no equation given and it is not expected that students will write the equation (although this may be possible); rather, students are expected to determine important features of the function directly from the graph of the derivative. They may be asked for the location of extreme values, intervals where the function is increasing or decreasing, concavity, etc. They may be asked for function values at points.

The graph may be given in context and student will be asked about that context. The graph may be identified as the velocity of a moving object and questions will be asked about the motion and position. (Type 2)

Less often the function’s graph may be given and students will be asked about its derivatives.

What students should be able to do:

Read information about the function from the graph of the derivative. This may be approached by derivative techniques or by antiderivative techniques.
Find and justify where the function is increasing or decreasing.
Find and justify extreme values (1^st and 2^nd derivative tests, Closed interval test aka. Candidates’ test).
Find and justify points of inflection.
Find slopes (second derivatives, acceleration) from the graph.
Write an equation of a tangent line.
Evaluate Riemann sums from geometry of the graph only.
FTC: Evaluate integral from the area of regions on the graph.
FTC: The function, g(x), maybe defined by an integral where the given graph is the graph of the integrand, f(t), so students should know that if, $\displaystyle g\left( x \right)=g\left( a \right)+\int_{a}^{t}{f\left( t \right)dt}$ then ${g}'\left( x \right)=f\left( x \right)$ and ${{g}'}'\left( x \right)={f}'\left( x \right)$ . In this case students should write ${g}'(t)=f\left( t \right)$ on their answer paper, so it is clear to the reader that they understand this.

Not only must students be able to identify these things, but they are usually asked to justify their answer and reasoning. See Writing on the AP Exams for more on justifying and explaining answers.

The ideas and concepts that can be tested with this type question are numerous. The type appears on the multiple-choice exams as well as the free-response. They have accounted for almost 20% of the points available on recent tests. It is very important that students are familiar with all the ins and outs of this situation.

As with other questions, the topics tested come from the entire year’s work, not just a single unit. In my opinion many textbooks do not do a good job with these topics.

Study past exams; look them over and see the different things that can be asked.

For some previous posts on this subject see October 15, 17, 19, 24, 26 (my most read post), 2012 and January 25, 28, 2013

An activity on this topic is here. The first pages are the teacher’s copy and solution. Then there are copies for Groups A, B, and C. Divide your class into 3 or 6 or 9 groups and give one copy to each. After they complete their activity have the students compare their results with the other groups.

Added 4-1-17

Tuesday March 14: Area and Volume (Type 4)

Friday March 17: Table and Riemann sums (Type 5)

Tuesday Match 21: Differential Equations (Type 6)

Friday March 24: Others (Type 7: related rates, implicit differentiation, etc.)

Is this going to be on the exam?

Posted on December 20, 2016 by Lin McMullin

Recently there was a discussion on the AP Calculus Community bulletin board regarding whether it was necessary or desirable to have students do curve sketching starting with the equation and ending with a graph with all the appropriate features – increasing/decreasing, concavity, extreme values etc., etc. – included. As this is kind of question that has not been asked on the AP Calculus exam, should the teacher have his students do problems like these?

The teacher correctly observed that while all the individual features of a graph are tested, students are rarely, if ever, expected to put it all together. He observed that making up such questions is difficult because getting “nice” numbers is difficult.

Replies ran from No, curve sketching should go the way of log and trig tables, to Yes, because it helps connect f. f ‘ and f ‘’, and to skip the messy ones and concentrate on the connections and why things work the way they do. Most people seemed to settle on that last idea; as I did. As for finding questions with “nice” numbers, look in other textbooks and ~~steal~~ borrow their examples.

But there is another consideration with this and other topics. Folks are always asking why such-and-such a topic is not tested on the AP Calculus exam and why not.

The AP Calculus program is not the arbiter of what students need to know about first-year calculus or what you may include in your course. That said, if you’re teaching an AP course you should do your best to have your students learn everything listed in the 2019 Course and Exam Description book and be aware of how those topics are tested – the style and format of the questions. This does not limit you in what else you may think important and want your students to know. You are free to include other topics as time permits.

Other considerations go into choosing items for the exams. A big consideration is writing questions that can be scored fairly. Here are some thoughts on this by topic.

Curve Sketching

If a question consisted of just an equation and the directions that the student should draw a graph, how do you score it? How accurate does the graph need to be? Exactly what needs to be included?

An even bigger concern is what do you do if a student makes a small mistake, maybe just miscopies the equation? The problem may have become easier (say, an asymptote goes missing in the miscopied equation and if there is a point or two for dealing with asymptotes – what becomes of those points?) Is it fair to the student to lose points for something his small mistake made it unnecessary for him to consider? Or if the mistake makes the question so difficult it cannot be solved by hand, what happens then? Either way, the student knows what to do, yet cannot show that to the reader.

To overcome problems like these, the questions include several parts usually unrelated to each other, so that a mistake in one part does not make it impossible to earn any subsequent points. All the main ideas related to derivatives and graphing are tested somewhere on the exam, if not in the free-response section, then as a multiple-choice question.

(Where the parts are related, a wrong answer from one part, usually just a number, imported into the next part is considered correct for the second part and the reader then can determine if the student knows the concept and procedure for that part.)

Optimization

A big topic in derivative applications is optimization. Questions on optimization typically present a “real life” situation such as something must be built for the lowest cost or using the least material. The last question of this type was in 1982 (1982 AB 6, BC 3 same question). The question is 3.5 lines long and has no parts – just “find the cost of the least expensive tank.”

The problem here is the same as with curve sketching. The first thing the student must do is write the equation to be optimized. If the student does that incorrectly, there is no way to survive, and no way to grade the problem. While it is fair to not to award points for not writing the correct equation, it is not fair to deduct other points that the student could earn had he written the correct equation.

The main tool for optimizing is to find the extreme value of the function; that is tested on every exam. So here is a topic that you certainly may include the full question in you course, but the concepts will be tested in other ways on the exam.

The epsilon-delta definition of limit

I think the reason that this topic is not tested is slightly different. If the function for which you are trying to “prove” the limit is linear, then 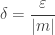$\displaystyle \delta =\frac{\varepsilon }{\left| m \right|}$ where m is the slope of the line – there is nothing to do beside memorize the formula. If the function is not linear, then the algebraic gymnastics necessary are too complicated and differ greatly depending on the function. You would be testing whether the student knew the appropriate “trick.”

Furthermore, in a multiple-choice question, the distractor that gives the smallest value of must be correct (even if a larger value is also correct).

Moreover, finding the epsilon-delta relationship is not what’s important about the definition of limit. Understanding how the existence of such a relationship say “gets closer to” or “approaches” in symbols and guarantees that the limit exists is important.

Volumes using the Shell Method

I have no idea why this topic is not included. It was before 1998. The only reason I can think of is that the method is so unlike anything else in calculus (except radial density), that it was eliminated for that reason.

This is a topic that students should know about. Consider showing it too them when you are doing volumes or after the exam. Their college teachers may like them to know it.

Integration by Parts on the AB exam

Integration by Parts is considered a second semester topic. Since AB is considered a one-semester course, Integration by Parts is tested on the BC exam, but not the AB exam. Even on the BC exam it is no longer covered in much depth: two- or more step integrals, the tabular method, and reduction formulas are not tested.

This is a topic that you can include in AB if you have time or after the exam or expand upon in a BC class.

Newton’s Method, Work, and other applications of integrals and derivatives

There are a great number of applications of integrals and derivatives. Some that were included on the exams previously are no longer listed. And that’s the answer right there: in fairness, you must tell students (and teachers) what applications to include and what will be tested. It is not fair to wing in some new application and expect nearly half a million students to be able to handle it.

Also, remember when looking through older exams, especially those from before 1998, that some of the topics are not on the current course description and will not be tested on the exams.

Solution of differential equations by methods other than separation of variables

Differential equations are a huge and important area of calculus. The beginning courses, AB and BC, try to give students a brief introduction to differential equations. The idea, I think, is like a survey course in English Literature or World History: there is no time to dig deeply, but the is an attempt to show the main parts of the subject.

While the choices are somewhat arbitrary, the College Board regularly consults with college and university mathematics departments about what to include and not include. The relatively minor changes in the new course description are evidence of this continuing collaboration. Any changes are usually announced two years in advance. (The recent addition of density problems unannounced, notwithstanding.) So, find a balance for yourself. Cover (or better yet, uncover) the ideas and concepts in the course description and if there if a topic you particularly like or think will help your students’ understanding of the calculus, by all means include it.

PS: Please scroll down and read Verge Cornelius’ great comment below.

Happy Holiday to everyone. There is no post scheduled for next week; I will resume in the new year. As always, I like to hear from you. If you have anything calculus-wise you would like me to write about, please let me know and I’ll see what I can come up with. You may email me at lnmcmullin@aol.com

Good Question 10 – The Cone Problem

Posted on November 8, 2016 by Lin McMullin

Today’s good question is an optimization problem, but its real point is choosing how to do the computation. As such it relates to MPAC 3a and 3b: “Students can … select appropriate mathematical strategies [and] sequence algebraic/computational processes logically.” The algebra required to solve this questions can be quite daunting, unless you get clever. Here’s the question.

A sector of arc length x is removed from a circle of radius 10 cm. The remaining part of the circle is formed into a cone of radius r and height h,

Find the value of x so that the cone has the maximum possible volume.

The sector that was removed is also formed into a cone. Find the value of x that makes this cone have it maximum possible volume. (Hint: This is an easy problem.)

In the context of the problem, the expression for the volume of the cone in part a. has a domain of $0\le x\le 20\pi$ . Why? Ignore the physical situation and determine the domain of the expression for the volume from a. Graph the function. Discuss.

Solutions:

Part a: As usual, we start by assigning some variables.

Let r be the radius of the base of the cone and let h be its height. The circumference of the cone is $2\pi r=20\pi -x$ , so $r=10-\frac{x}{2\pi }$ and $h=\sqrt{{{10}^{2}}-{{r}^{2}}}$ . The volume of the cone is

$\displaystyle V=\frac{\pi }{3}{{r}^{2}}h=\frac{\pi }{3}{{r}^{2}}\sqrt{{{10}^{2}}-{{r}^{2}}}=\frac{\pi }{3}{{\left( 10-\frac{x}{2\pi } \right)}^{2}}\sqrt{{{10}^{2}}-{{\left( 10-\frac{x}{2\pi } \right)}^{2}}}$

To find the maximum, the next step is to differentiate the volume. The expression on the right above looks way complicated and its derivative will be even worse. Simplifying it is also a lot of trouble, and, in fact, does not make things easier.* Here’s where we can be clever and avoid a lot of algebra. Let’s just work from $\displaystyle V=\frac{\pi }{3}{{r}^{2}}\sqrt{{{10}^{2}}-{{r}^{2}}}$

To find the maximum differentiate the volume with respect to x using the chain rule.

$\displaystyle \frac{dV}{dx}=\frac{dV}{dr}\cdot \frac{dr}{dx}=\frac{\pi }{3}\left( {{r}^{2}}\frac{-2r}{2\sqrt{{{10}^{2}}-{{r}^{2}}}}+2r\sqrt{{{10}^{2}}-{{r}^{2}}} \right)\left( -\frac{1}{2\pi } \right)$

Setting this equal to zero and simplifying (multiply by $-6\sqrt{{{10}^{2}}-{{r}^{2}}}$ ) gives

$-{{r}^{3}}+2r\left( 100-{{r}^{2}} \right)=200r-3{{r}^{3}}=0$

$\displaystyle r=0,r=\sqrt{\frac{200}{3}}=\frac{10\sqrt{6}}{3}$

The minimum is obviously r = 0, so the maximum occurs when $\displaystyle r=10-\frac{x}{2\pi }=\frac{10\sqrt{6}}{3}$ . Then, solving for x gives

$\displaystyle x=2\pi \left( 10-\frac{10\sqrt{6}}{3} \right)\approx 11.52986$

Aside: We often see questions saying, if y = f(u) and u = g(x), find dy/dx. Here we have put that idea to practical use to save doing a longer computation.

Part b: The arc of the piece cut out is the circumference, x, of a cone with a radius of $\displaystyle {{r}_{1}}=\frac{x}{2\pi }$ and a height of $\displaystyle {{h}_{1}}=\sqrt{{{10}^{2}}-{{r}_{1}}^{2}}$ . Its volume is

$\displaystyle V=\frac{\pi }{3}{{r}_{1}}^{2}\sqrt{{{10}^{2}}-{{r}_{1}}^{2}}$

This is the same as the expression we used in part a. and can be handled the same way, except that here $\displaystyle \frac{d{{r}_{1}}}{dx}=+\frac{1}{2\pi }$ . The computation and result will be the same. The result will be the same. The maximum occurs at

$\displaystyle x=2\pi \left( 10-\frac{10\sqrt{6}}{3} \right)\approx 11.52986$

This should not be a surprise. The piece cut out and the piece that remains are otherwise indistinguishable, so the maximum volume should be the same for both.

Part c: From part a we have $\displaystyle V=\frac{\pi }{3}{{r}^{2}}\sqrt{{{10}^{2}}-{{r}^{2}}}=\frac{\pi }{3}{{\left( 10-\frac{x}{2\pi } \right)}^{2}}\sqrt{{{10}^{2}}-{{\left( 10-\frac{x}{2\pi } \right)}^{2}}}$ . To graph there is no need to simplify the expression in x:

$Tthe x scale marks are at multiples of $latex 5\pi $$

The x-scale marks are at multiples of $5\pi$

The domain is determined by the expression under the radical so

$-10\le r\le 10$

$-10\le 10-\frac{x}{2\pi }\le 10$

$0\le x\le 40\pi$

This is the “natural domain” of the function without regard to the physical situation given in the original problem. I cannot think of a reason for the difference.

________________

*Fully simplified in terms of x the volume is $\displaystyle V=\frac{1}{24{{\pi }^{2}}}{{\left( 20\pi -x \right)}^{2}}\sqrt{40\pi x-{{x}^{2}}}$ . This isn’t really easier to differentiate and solve.

From One Side or the Other.

Posted on November 1, 2016 by Lin McMullin

Recently, a reader wrote and suggested my post on continuity would be improved if I discussed one-sided continuity. This, along with one-sided differentiability, is today’s topic.

The definition of continuity requires that for a function to be continuous at a value x = a in its domain $\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=f\left( a \right)$ and that both values are finite. That is, the limit as you approach the point in question be equal to the value at that point. This limit is a two-sided limit meaning that the limit is the same as x approaches a from both sides. That definition is extended to open intervals, by requiring that for a function to be continuous on an open interval, that it is continuous at every point of the interval

How do you check every point? One way is to prove the limit in the definition in general for any point in the open interval. Another is to develop a list of theorems that allow you to do this. For example, f(x) = x can be shown to be continuous at every number. Then sums, differences, and products, of this function allows you to extend the property to polynomials and then other functions.

But what about a function that has a domain that is not the entire number line? Something like $f\left( x \right)=\sqrt{4-{{x}^{2}}},-2\le x\le 2$ . Here, $f\left( -2 \right)=f\left( 2 \right)=0$ ; the function is defined at the endpoints. A look at the graph shows a semi-circle that appears to contain the endpoints (–2, 0) and (2, 0). The function is continuous on the open interval (–2, 2) but cannot be continuous under the regular definition since the limit at the endpoints does not exist. The limit does not exist because the limit from the left at the left-endpoint, and the limit from the right at the right endpoint do not exist. What to do?

What is done is to require only that the one-sides limits from inside the domain exist. Here they do: $\underset{x\to -2+}{\mathop{\lim }}\,f\left( x \right)=0$ and the $\underset{x\to 2-}{\mathop{\lim }}\,f\left( x \right)=0$ and since the limits equal the values we say the function is continuous on the closed interval [–2, 2]. In general, when you say a function is continuous on a closed interval, you mean that the one-sided limits from inside the interval exist and equal the endpoint values.

You can determine that the limits exist by finding them as in the example above. Another way is to realize that if a < b < c < d and the function is continuous on the open (or closed) (a, d) then it is continuous on the closed interval [b c].

Why bother?

The reason we take this trouble is because for some reason the proof of the theorem under consideration requires that the endpoint value not only exist but hooks up with the function to make it continuous. Thus, the continuity on a closed interval is included in the hypotheses of theorem where this property is required. For example, the Intermediate Value Theorem would not work on a function that had no endpoints for $f\left( c \right)$ to be between. Also, the Mean Value Theorem requires you to find the slope between the endpoints, so the endpoint needs to be not only defined, but attached to the rest of the function.

One-sided differentiability

The definition of the derivative at a point also requires a two-sided limit to exist at the point. Most of the early theorems in calculus require only that the function be differentiable on an open interval.

Is it possible to define differentiability at the endpoint of an interval? Yes. It’s done in the same way by using a one-sided limit. If x = a is the left endpoint of an interval, then the derivative from the right at that point is defined as

$\displaystyle {f}'\left( a \right)=\underset{h\to 0+}{\mathop{\lim }}\,\frac{f\left( a+h \right)-f\left( a \right)}{h}$ .

By letting h approach 0 only from the right, you never consider values outside the interval. (At the right endpoint a similar definition is used with $h\to 0-$ ).

So why don’t we ever see one-sided derivatives? Because the theorems do not need them to prove their result. Hypotheses of theorems should be the minimum requirements needed, so if there is no need for the function to be differentiable at an endpoint, this is not listed in the hypotheses. This makes the hypothesis less restrictive and, therefore, covers more situations.

One theorem, beyond what is usually covered in beginning calculus, where endpoint differentiability is needed is Darboux’s Theorem. Darboux’s Theorem is sometime called the Intermediate Value Theorem for derivatives. It says that the derivative takes on all values between the derivatives at the endpoints, and thus needs the one-sided derivatives at the endpoints to exist. Interestingly, Darboux’s Theorem does not require the function to be continuous on the open interval between the endpoints.

How to Tell your Asymptote from a Hole in the Graph.

Posted on October 4, 2016 by Lin McMullin

The fifth in the Graphing Calculator / Technology series

(The MPAC discussion will continue next week)

Seeing discontinuities on a graphing calculator is possible; but you need to know how a calculator graphs to do it. Here’s the story:

The number you choose for XMIN becomes the x-coordinate of the (center of) the pixels in the left most column of pixels. The number you choose for XMAX is the x-coordinate of the right most column of pixels. The distance between XMIN and XMAX is divided evenly between the remaining pixels so that all the pixels are evenly spaced across the screen (the same distance apart). The rows of pixels are done the same way evenly spacing them between YMIN and YMAX.

This spacing is usually not at “nice” values as can be seen by just moving the cursor across the screen and noticing the x-values or y-values at the bottom of the screen.

The cursor is located one pixel to the right of the y-axis and one pixel above the x-axis in the “standard” window of a TI-8x. Note the coordinates of that pixel at the bottom of the screen. These are the distances between the pixels.

To draw a graph, the calculator takes the x-coordinate of each pixel, calculates the corresponding y-value and turns on the pixel in that column with closest y-pixel-coordinate. If set in a connect mode, the calculator turns on several pixels in adjacent columns so that the y-values seem to connect; this is why the graph often looks jagged in steep sections of the graph. If you are in DOT mode, this does not happen and only one pixel in each column is on.

If you move the cursor over one of the points on a graph, you will see the pixel coordinates, NOT the actual y-coordinates. Use TRACE to see the actual y-coordinate. This is why when finding intersections, you should not just move the cursor over the point, but rather use “intersect” to see the actual y-value of the function.

If the function is undefined for some x-pixel value, then no pixel will turn on in that column. If the function is undefined for some value between the pixel values, then nothing happens because the calculator has not evaluated the function there, so the graph seems to be continuous.

Vertical “asymptotes” are the result of the calculator not evaluating the function at the undefined value; rather it connects the value on one side of the asymptote off the bottom of the screen with the next value on the other side of the asymptote off the top of the screen. If the asymptote appears exactly at a pixel value, then no “asymptote” will appear and that column of pixels will have no pixel turned on. (Some newer calculators and newer operating systems on older calculators have made adjustments so that the “asymptotes” do not show up. In some systems this feature can be turned on or off.)

$The function $latex \displaystyle y=\frac{3\left( x-2 \right)}{\left( x-2 \right)\left( x+2 \right)}$ in the standard window. The vertical line is not really the asymptote and the “hole” at (2, 0.75) is not seen.$

The function $\displaystyle y=\frac{3\left( x-2 \right)}{\left( x-2 \right)\left( x+2 \right)}$ in the standard window. The vertical line is not really the asymptote and the “hole” at (2, 0.75) is not seen.

A removable discontinuity, a hole in the graph (really a skipped pixel), can be seen, if it occurs at a pixel value. Since in most examples the hole is at an integer or other “nice” number, you will not see them in the “standard” window. Use a “decimal” window, which has been chosen in advance so the x-values of the pixels are integers and nice decimals. (To see this, in a decimal window move the cursor around and notice the pixel coordinates).

The other thing you can do is adjust the XMIN and XMAX values so that the distance between them will land on integer values. (Nice project for your class – the number of pixels can be found in the guidebook, or you can count them. In the old days, before decimal windows, this was necessary – it was called finding a “friendly window.”)

$The function $latex \displaystyle y=\frac{3\left( x-2 \right)}{\left( x-2 \right)\left( x+2 \right)}$ in the “decimal” window. The “asymptote” is not shown and the “hole” at (2, 0.75) is visible.$

The function $\displaystyle y=\frac{3\left( x-2 \right)}{\left( x-2 \right)\left( x+2 \right)}$ in the “decimal” window. The “asymptote” has disappeared and the “hole” at (2, 0.75) is now visible.

Zooming in or out may change these values so the hole or asymptote disappears.

For a related idea see the post My Favorite Function

PLEASE NOTE: I have no control over the advertising that appears on this blog. It is provided by WordPress and I would have to pay a great deal to not have advertising. I do not endorse anything advertised here. I noticed that ads for one of the presidential candidates occasionally appears; I certainly do not endorse him.

Comparing the Graph of a Function and its Derivative

Posted on September 6, 2016 by Lin McMullin

The fourth in the Graphing Calculator / Technology series

Comparing the graph of a function and its derivative is instructive and necessary in beginning calculus. Today I will show you how you can do this first with Desmos a free online graphing program and then on a graphing calculator. Desmos does this a lot better than graphing calculators, because of the easy use of sliders. CAS calculators also have sliders but they are not as easy to use as Desmos.

Let’s get started. Instead of presenting you with a completed Desmos graph, I will show you how to make you own. One of the things I have found over the years is that it takes some mathematical knowledge to make good demonstration graph and that in itself if useful and instructive. Hopefully, you and your students will soon be able to make your own to show exactly what you want.

Open Desmos and sign into your account; if you don’t have one then register – its free and you can keep your results and even share them with others.

In the first entry line on the left, enter the equation of the function whose graph you want to explore. Call it f(x); that is enter f(x) = your function. Later you will be able to change this to other functions and investigate them, without changing anything else.

On the second line enter the symmetric difference quotient as

$\displaystyle s\left( x \right)=\frac{f\left( x+0.001 \right)-f\left( x-0.001 \right)}{2\left( 0.001 \right)}$

Instead of a variable h, as we did in our last post in this series, enter 0.001. This will graph the derivative without having to calculate the derivative. Of course, you could enter the derivative here if your class has learned how to calculate derivatives. If so, you will have to change this line each time you change the function.

In order to closely compare the function and its derivative, on the next line enter the equation of a vertical segment from a point on the function (a, f(a)) to a point on the derivative (a, s(a)). Desmos does not have a segment operation, but here is how you graph a segment. In general, a segment from (a, b) to (c, d) is entered as the parametric/vector function

$\left( a\cdot t+c\cdot \left( 1-t \right),b\cdot t+d\cdot \left( 1-t \right) \right),\ 0\le t\le 1$

The a, b, c, and d may be numbers or functions. Since our segment is vertical the first coordinate will have a = c and will reduce to a. Here’s what to enter on the third line:

$\left( a,f\left( a \right)\cdot t+s\left( a \right)\cdot \left( 1-t \right) \right)$

(Notice that there is no x in this expression; t is the variable. Also, the f(a) and s(a) may be interchanged.)

When you push enter, you will be prompted to add a slider for a: click to add the slider. A line will appear under the expression which will allow you to set the domain for t: click the endpoints and enter 0 on the left and 1 on the right, if necessary.

That’s it. You’re done. Use the slider to move around the graphs.

Using the graphs

Discuss with your class, or better yet divide them into groups and let them discuss, what they see. Since at this point they are probably new to this provide some hints such as “What happens on the graph of f when s is 0?” or “What is true on s when f is increasing?” or “What happens to the function at the extreme values of the derivative?” Prompt the students to look for increasing and decreasing, concavity, points of inflection, and extreme values. All the usual stuff. Work from the function to the derivative and from the derivative to the function.

Have your students formulate their results as (tentative) theorems. You actually want them to make some mistakes here, so you can help them improve their thinking and wording. For example, one result might be: If the function is increasing, then the derivative is positive. By changing the first function to an example like f(x) = x³ or f(x) = x + sin (x). Help them see that non-negative might be a better choice.

You might try giving different groups different functions and let them compare and contrast their results.

This is very much in line with MPACs 1, 2, 4, and 6.

You can do the same kind of thing with graphing calculators. That is, you can graph the function and its derivative or a difference quotient. The difference is that graphing calculators do not have sliders.

Extra feature: Desmos will graph a point if you enter the coordinates just like you write them: (a, b). The coordinates may be numbers or functions or a combination of both. Try adding two points to your graph one at each the end of the segment between the graphs that will move with the same slider.

f(x) = x + 2sin(x) and its derivative.

Teaching Calculus

The pleasure lies not in discovering the truth, but in searching for it.

Category Archives: Derivatives

Graph Analysis (Type 3)

Is this going to be on the exam?

Good Question 10 – The Cone Problem

From One Side or the Other.

How to Tell your Asymptote from a Hole in the Graph.

Comparing the Graph of a Function and its Derivative

Using the graphs

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Using the graphs

Share this: