Monthly Archives: January 2016

February 2016

Posted on by
Reply

As I hope you’ve noticed there is a new pull-down on the navigation bar called “Website.” For some years I’ve had a website at linmcmullin.net that lately I’ve been neglecting. I decided to close it in the next few days, and therefore, I move most of the material that is there to this new tab. The main items of interest are probably those under “Calculus”, “Winplot”, and “CAS.” If you used that website you should be able to find what you need here. If you cannot find something, then please write and I’ll try to help.

In my post entitled January 2016 are listing of post for the applications of integration for both AB and BC calculus. This month’s posts are BC topics on sequences, series, and parametric and polar equations.

Posts from past Februarys

Sequences and Series

February 9, 2015 Amortization A practical application of sequences.

February 8, 2013: Introducing Power Series 1

February 11, 2013: Introducing Power Series 2

February 13, 2013: Introducing Power Series 3

February 15, 2013 New Series from Old 1

February 18, 2013: New Series from Old 2

February 20, 2013: New Series from Old 3

February 22, 2013: Error Bounds

May 20, 2015 The Lagrange Highway

Polar, Parametric, and Vector Equations

March 15, 2013 Parametric and Vector Equations

March 18, 2013 Polar Curves

May 17, 2014 Implicit Differentiation of Parametric Equations 

A series on ROULETTES some special parametric curves (BC topic – enrichment):

 

 

 

 

 

What’s Your Favorite?

Posted on by
Reply

A very short post today. Audrey Weeks, author of Calculus in Motion, sent me this link to a BBC article by Melissa Hogenboom discussing the 10 most beautiful equations. Each equation can be clicked for more details and some of the links even have videos discussing the equation. Click here for You decide: What is the most beautiful equation? After reading about them, you can vote for your favorite and see the results so far.

beautiful equations

Good Question 8 – or not?

Posted on by
Reply

Seattle rainToday’s question is not a good question. It’s a bad question.

But sometimes a bad question can become a good one.

This one leads first to a discussion of units, then to all sorts of calculus.

Here’s the question a teacher sent me this week taken from his textbook:

The normal monthly rainfall at the Seattle-Tacoma airport can be approximated by the model R=3.121+2.399\sin \left( 0.524t+1.377 \right), where R is measured in inches and t is the time in months, t = 1 being January. Use integration to approximate the normal annual rainfall.  Hint: Integrate over the interval [0,12].

Of course, with the hint it’s not difficult to know what to do and that makes it less than a good question right there. The answer is 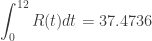\displaystyle \int_{0}^{12}{R(t)dt=37.4736} inches. You could quit here and go on to the next question, but …

Then a student asked. “If R is in inches shouldn’t be in units of the integral be inch-months, since the unit of an integral is the unit of the integrand times the units of the independent variable?”  Well, yes, they should. So, what’s up with that?

Also, the teacher figured that the integral of a rate is an amount and our answer is an amount, so why isn’t the integrand a rate?

The only answer I could come up with is that the statement “R is measured in inches” is incorrect; R should be measured in inches /month. The opening phrase “normal monthly rainfall” also seems to point to the correct units for R being inches/month.

Problem solved; or maybe does this lead to a different concern?

The teacher pointed out that R(6) = 0.7658 inches is a reasonable answer for the amount of rain in June whereas \displaystyle \int_{0}^{6}{R(t)dt=}20.4786 is not.

If R is a rate, then the amount of rain that falls in June (t = 6) is given by \displaystyle \int_{5}^{6}{R(t)dt}=0.9890.

From here on we will assume that R is a rate with units of inches/month. Here are the individual monthly rates calculated with a CAS. Ques 8 a

The total amount of rainfall (second line above) appears be R(1) + R(2) + R(3) + … +R(12) = 37.4742. This is very close to the amount calculated by integration.

The slight difference of 0.0006 is not a round off error.

Remember, behind every definite integral there is a Riemann sum!

Again, the units are the problem. Why does the sum of the monthly rates seem to give the total amount?  The reason is that the terms of the sequence above are actually the values of a right-side Riemann sum of the rate, R(t), over the interval [0,12] with 12 equal subdivisions of width 1 (month) each with the 1’s left out as 1’s often are. Therefore, their sum should come close to the total yearly rainfall, but it is really just an approximation of it.

The actual total for any month, n, is given by \displaystyle \int_{n-1}^{n}{r(t)}dt. For example the amount of rain that falls in June is given by \displaystyle \int_{5}^{6}{R(t)dt}=0.9890 inches.

Here is the sequence of the actual monthly rainfall values in inches, and their sum.

Ques 8 b

This agrees with the integral. Why? Because one of  the properties of integrals tell us that \displaystyle \sum\limits_{n=1}^{12}{\int_{n-1}^{n}{r(t)dt}}=\int_{0}^{12}{r(t)dt}.

Another instructive thing with this integral is this: The function R=3.121+2.399\sin \left( 0.524t+1.377 \right) is periodic with a period of  \frac{2\pi }{0.524}\approx 11.9908\approx 12. So the sine function takes on (almost) all its values in a year, as you would expect. Since the sine values all but cancel each other out

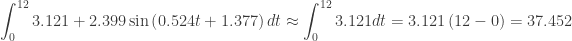\displaystyle \int_{0}^{12}{3.121+2.399\sin \left( 0.524t+1.377 \right)dt}\approx \int_{0}^{12}{3.121dt=3.121\left( 12-0 \right)=37.452}. Close!

The total rainfall divided by 12 is \frac{37.452}{12}=3.121 this must be close to the average rainfall each month. The average rainfall is \displaystyle \frac{1}{12}\int_{0}^{12}{R\left( t \right)dt}=3.1228 inches. Close, again!

So, there you have it. Is this a good question or not? We considered all these concepts while working not just with an equation but with numbers from a poorly stated problem:

  • Reading and interpreting words.
  • Unit analysis
  • Integration by technology
  • Realizing that a pretty good approximation is not correct, due again to units.
  • A Riemann sum approximation in a real situation that comes very close to the value by integration
  • Using a property of a periodic function to greatly simplify an integral
  • Finding average value two ways

So, it turned out to be a sunny day in Seattle.seattle sun

.

January 2016

Posted on by
Reply

HAPPY NEW YEAR

– a few more days off and then back to school!

If you haven’t already, it is time to start integration. The posts on starting integration were listed in December since I try to stay ahead of things so you’ll have time to prepare. With that in mind here are past posts on applications of integration – area, volume, average value, improper integrals, accumulation, and some enrichment for BC classes on parametric equations. This will take AB courses well into February. The February postings will be for the BC topics on sequences and series.

The four featured post below are the most popular from this list.

Applications of integration: area, volume, average value of a function, Accumulation and functions defined by integrals.

January 2, 2013 Integration by Parts – 1

January 4, 2013 Integration by Parts – 2

January 7, 2013 Area Between Curves

 A series on visualizing solid figures:Solid rotation

January 9, 2013 Volume of Solids with Regular Cross-sections

January 11, 2013 Volumes of Revolution

January 14, 2013 Why You Never Need Cylindrical Shells

January 25, 2014 Improper Integrals and proper areas.

January 16, 2013 Average Value of a Function

February 6, 2013: Logarithms

January 19, 2013 Most Triangles are Obtuse! What is the probability that a triangle picked at random will be acute? An average value problem solved by a tenth grader.

 A series on ROULETTES some special parametric curves (BC topic – enrichment):

Accumulation – On the exams; not in many textbooks 

.