Tag Archives: limits

Good Question 1: 2008 AB 6

Posted on by
4

When I started this blog several years ago I was hoping my readers would ask questions that we could discuss or submit ideas for additional topics to write about. This has not really happened, but I’m still very open to the idea. (That was a HINT.) Since that first year when I had the entire curriculum ahead of me, I have written less not because I dislike writing, but because I am low on ideas.

The other day, I answered a question posted on the AP Calculus Community bulletin board about AB calculus exam question. It occurred to me that this somewhat innocuous looking question was quite good. So I decided to start an occasional series on good questions, from AP exams or elsewhere, that can be used to teaching beyond the actual things asked in the question.  (My last post might be in this category, but that was written several months ago.)

In discussing these questions, I will make numerous comments about the question and how to take it further in your class. My idea is not just to show how to write a good answer, but rather to use the question to look deeper into the concepts involved.

Good Question #1: 2008 AB Calculus exam question 6.

The stem gave students the function \displaystyle f\left( x \right)=\frac{\ln \left( x \right)}{x},\quad x>0. Students were also told that \displaystyle {f}'\left( x \right)=\frac{1-\ln \left( x \right)}{{{x}^{2}}}.

  1. The first thought that occurs is why they gave the derivative. The reason is, as we will see, that the first derivative is necessary to answer the first three parts of the question. Therefore, a student who calculates an incorrect derivative is going to be in big trouble (and the readers may have a great deal of work to do reading with the student’s incorrect work). The derivative is calculated using the quotient rule, and students will have to demonstrate their knowledge of the quotient rule later in this question; there is no reason to ask them to do the same thing twice.
  2. If you are using this with a class, you can, and probably should, ask your students to calculate the first derivative. Then you can see how many giving the derivative would have helped.
  3. When discussing the stem, you should also discuss the domain, x > 0, and the x-intercept (1, 0). Other features of the graph, such as end behavior, are developed later in the question, so they may be put on hold briefly.

Part a asked students to write an equation of the tangent line at x = e2. To do this students need to do two calculations: \displaystyle f\left( {{e}^{2}} \right)=\frac{2}{{{e}^{2}}} and \displaystyle {f}'\left( {{e}^{2}} \right)=-\frac{1}{{{e}^{4}}}. An equation of the tangent line is \displaystyle y=\frac{2}{{{e}^{2}}}-\frac{1}{{{e}^{4}}}\left( x-{{e}^{2}} \right).

  1. Writing the equation of a tangent line is a very important skill and should be straightforward. The point-slope form is the way to go. Avoid slope-intercept.
  2. The tangent line is used to approximate the value of the function near the point of tangency; you can throw in an approximation computation here.
  3. After doing part c, you should return here and discuss whether the approximation is an overestimate or an underestimate and how you can tell. (Answer: underestimate, since the graph is concave up here.)
  4. After doing part c, you can also ask them to write the tangent line at the point of inflection and whether approximations near the point of inflection are overestimates or an underestimates, and why. (Answer: Since the concavity change here, it depends on which side of the point of inflection the approximation is made. To the left is an overestimate; to the right is an underestimate.)

Part b asked students to find the x-coordinate of the critical point, determine whether it is a maximum, a minimum, or neither, and to “justify your answer.” To earn credit students had to write the equation \displaystyle {f}'\left( x \right)=0 and solve it getting x = e. They had to state that this is a maximum because  “{f}'\left( x \right)changes from positive to negative at x = e.”

This is a very standard AP exam question. To expand it in your class:

  1. Discuss how you know the derivative changes sign here. This will get you into the properties of the natural logarithm function.
  2. Discuss why the change in sign tells you this is a maximum. (A positive derivative indicates an increasing function, etc.)
  3. After doing part c, you can return here and try the second derivative test.
  4. The question asks for “the” critical point, hinting that there is only one. Students should learn to pick up on hints like this and be careful if their computation produces more or less than one.
  5. At this point we have also determined that the function is increasing on the interval \left( -\infty ,e \right] and decreasing everywhere else. The question does not ever ask this, but in class this is worth discussing as important features of the graph. On why these are half-open intervals look here.

Part c told students there was exactly one point of inflection and asked them to find its x-coordinate.  To do this they had to use the quotient rule to find that \displaystyle {{f}'}'\left( x \right)=\frac{-3+2\ln \left( x \right)}{{{x}^{3}}}, set this equal to zero and find the x-coordinate to be x = e3/2.

  1. The question did not require any justification for this answer. In class you should discuss what a justification would look like. The reason is that the second derivative changes sign here. So now you need to discuss how you know this.
  2. Also, you can now determine that the function is concave down on the interval \left( -\infty ,{{e}^{3/2}} \right) and concave up on the interval \left({{e}^{3/2}},\infty \right). Ask your class to justify this.

Part d asked student to find \displaystyle \underset{x\to 0+}{\mathop{\lim }}\,\frac{\ln \left( x \right)}{x}. The answer is -\infty . While this seems almost like a throwaway tacked on the end because they needed another point, it is the reason I like this question.

  1. The question is easily solved: \displaystyle \underset{x\to 0+}{\mathop{\lim }}\,\frac{\ln \left( x \right)}{x}=\underset{x\to 0+}{\mathop{\lim }}\,\frac{1}{x}\cdot \underset{x\to 0+}{\mathop{\lim }}\,\ln \left( x \right)=\left( \infty \right)\left( -\infty \right)=-\infty .
  2. While tempting, the limit cannot be found by L’Hôpital’s Rule, because on substitution you get \frac{-\infty }{0},which is not one of the forms that L’Hôpital’s Rule can handle.
  3. The reason I like this part so much is that we have already developed enough information in the course of doing the problem to find this limit! The function is increasing and concave down on the interval \left( -\infty ,e \right). Moving from the maximum to the left, the function crosses the x-axis at (1, 0), keeps heading south, and gets steeper. So the limit as you approach the y-axis from the right is negative infinity.This is the left-side end behavior.
  4. What about the right-side end behavior? (You ask your class.) Well, the function is positive and decreasing to the right of the maximum and becomes concave up after x = e3/2. Thus, it must flatten out and approach the x-axis as an asymptote.
  5. That \displaystyle \underset{x\to \infty }{\mathop{\lim }}\,\frac{\ln \left( x \right)}{x}=0 is clear from the note immediately above. This limit can be found by L’Hôpital’s Rule since it is an indeterminate of the type \infty /\infty . So, \displaystyle \underset{x\to \infty }{\mathop{\lim }}\,\frac{\ln \left( x \right)}{x}=\underset{x\to \infty }{\mathop{\lim }}\,\frac{\tfrac{1}{x}}{1}=0.
  6. Notice also that the first derivative approaches zero as x approaches infinity. This indicates that the function’s graph approaches the horizontal as you travel farther to the right. The second derivative also approaches zero as x approaches infinity indicating that the function’s graph is becoming flatter (less concave).

This question and the discussion is largely done analytically (working with equations). We did find a few important numbers in the course of the work. Hopefully, you students discussed this with many good words. To complete the Rule of Four, here is the graph.

2008 AB 6 - 1

And here is a close up showing the important features of the graph and the corresponding points on the derivatives.

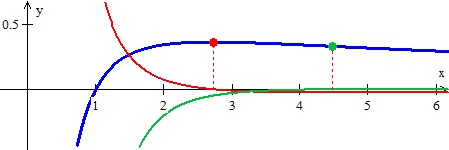
The function is shown in blue, the derivative and maximum in red, and the second derivative and the point of inflection in green.

The function is shown in blue, the derivative and maximum in red, and the second derivative and the point of inflection in green.

Finally, this function and the limit at infinity is similar to the more pathological example discussed in the post of October 31, 2012 entitled Far Out!

Continuity 2

Posted on by
2

The definition of continuity of a function used in most first-year calculus textbooks reads something like this:

A function f is continuous at x = a if, and only if,

(1) f(a) exists (the value is a finite number),

(2) \underset{x\to a}{\mathop{\lim }}\,f\left( x \right) exists (the limit is a finite number), and

(3) \underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=f\left( a \right) (the limit equals the value).

A function is continuous on an interval if, and only if, it is continuous at all values of the interval. For the endpoints of closed intervals, the limits are adjusted to one-sided limits with x approaching a from inside the interval.

As I’ve written before, limits logically come before continuity since limits are used in the definition of continuity. But as a practical and historical matter continuity comes first. Continuity, or rather lack of continuity, gives us the examples that motivate the need for the concept of limit.

Karl Weierstrass (1815 – 1897) gave the modern definition of continuity: Given a function f and an element a of the domain I,   f is said to be continuous at the point a if for any number \varepsilon >0, however small, there exists a number \delta >0 such that for all x in the domain of f,  \left| x-a \right|<\delta  implies \left| f\left( x \right)-f\left( a \right) \right|<\varepsilon .

This looks very much like the definition of limit. In the delta-epsilon definition of limit the last inequality above is \left| f\left( x \right)-L \right|<\varepsilon  where L is the limit. Replacing the value with the limit allows a somewhat simpler wording of the definition of continuity than that given at the beginning, but adds the delta-epsilon complication. Weierstrass’ definition eliminates the need for saying the value and the limit are finite since that is assumed by writing f (a).

Some textbooks use the phrase “a function is continuous on its domain.” This seems somewhat limiting (no pun intended) in that a function such as \displaystyle f\left( x \right)=\tfrac{1}{x} is certainly continuous on its domain but not continuous on the entire number line. We are usually concerned about where a function is not continuous, so first we find where it is not continuous: at the points not in its domain plus possibly other points in its domain.

Recent AP calculus exams (2012 AB4c, 2011 AB 6a) gave students a piecewise defined function and asked if it is continuous at the point where the two pieces meet. The question directed students to “use the definition of continuity to explain your answer” and “show that f is continuous.”  To answer the question students were expected to state what the two one-sided limits are and what the value there is. Since all these numbers are finite and equal the requirements of the definition are met.

This kind of question could be considered a question about continuity or a question about applying a definition (or theorem) to a particular situation. Either way students should understand the hypotheses of a definition or theorem and know how to verify that they are met in a particular situation.

Locally Linear L’Hôpital

Posted on by
1

I’ll begin with a lemma. (I like to do a lemma now and then if for no other reason than having an excuse to explain what a lemma is – a simple theorem that is used in proving the main theorem.)

Lemma: If two lines intersect on the x-axis, then for any x the ratio of their y-coordinates is equal to the ratio of their slopes.

Proof: Two lines with slopes of m1 and m2 that intersect at (a, 0) on the x-axis have equations y1 = m1(x – a) and y2 = m2(x – a). Then

\displaystyle \frac{{{y}_{1}}}{{{y}_{2}}}=\frac{{{m}_{1}}\left( x-a \right)}{{{m}_{2}}\left( x-a \right)}=\frac{{{m}_{1}}}{{{m}_{2}}}

L’Hôpital’s Rule (Theorem): If f and g are differentiable near x = a and f(a) = g(a) = 0, then

\displaystyle \underset{x\to a}{\mathop{\lim }}\,\frac{f\left( x \right)}{g\left( x \right)}=\underset{x\to a}{\mathop{\lim }}\,\frac{{f}'\left( x \right)}{{g}'\left( x \right)}

if the limit exists.

The fact that f(a) = g(a) = 0 means that the two functions intersect on the x-axis at (a, 0). For example, the functions f(x) = tan(x) and g(x) = sin(x) have this property at \left( \pi ,0 \right).

Figure 1. y = tan(x) in red and y = sin(x) in blue

Figure 1. y = tan(x) in red and y = sin(x) in blue

Now zoom-in several times centered at \left( \pi ,0 \right).

Figure 2. The previous graph zoomed in.

Figure 2. The previous graph zoomed in.

Whoa!

That looks like lines!!

It’s the local linearity property of differentiable functions – if you zoom-in enough any differentiable function eventually looks linear. So maybe near \left( \pi ,0 \right) the lemma applies. The only difference is that the slopes of the “lines” are the derivatives so

\displaystyle \underset{x\to a}{\mathop{\lim }}\,\frac{f\left( x \right)}{g\left( x \right)}=\underset{x\to a}{\mathop{\lim }}\,\frac{{f}'\left( x \right)}{{g}'\left( x \right)}

 Now that does not quite prove L’Hôpital’s Rule, but it should give you and your students a good idea of why L’Hôpital’s Rule is true.

Then in our example:

\displaystyle \underset{x\to \pi }{\mathop{\lim }}\,\frac{\tan \left( x \right)}{\sin \left( x \right)}=\underset{x\to \pi }{\mathop{\lim }}\,\frac{\frac{1}{{{\left( \cos \left( x \right) \right)}^{2}}}}{\cos \left( x \right)}=\underset{x\to \pi }{\mathop{\lim }}\,\frac{1}{{{\left( \cos \left( x \right) \right)}^{3}}}=\frac{1}{{{\left( \cos \left( \pi \right) \right)}^{3}}}=-1

But isn’t that obvious from Figure 2?

Think about it.

More on this next time.

 

 

 

 

 

Why Radians?

Posted on by
26

Calculus is always done in radian measure. Degree (a right angle is 90 degrees) and gradian measure (a right angle is 100 grads) have their uses. Outside of the calculus they may be easier to use than radians. However, they are somewhat arbitrary. Why 90 or 100 for a right angle? Why not 10 or 217?

Radians make it possible to relate a linear measure and an angle measure. A unit circle is a circle whose radius is one unit. The one-unit radius is the same as one unit along the circumference. Wrap a number line counterclockwise around a unit circle starting with zero at (1, 0). The length of the arc subtended by the central angle becomes the radian measure of the angle.

This keeps all the important numbers like the sine and cosine of the central angle, on the same scale. When you graph y = sin(x) one unit in the x-direction is the same as one unit in the y-direction. When graphing using degrees, the vertical scale must be stretched a lot to even see that the graph goes up and down. Try graphing on a calculator y = sin(x) in degree mode in a square window and you will see what I mean.

But the utility of radian measure is even more obvious in calculus. To develop the derivative of the sine function you first work with this inequality (At the request of a reader I have added an explanation of this inequality at the end of the post):

\displaystyle \frac{1}{2}\cos \left( \theta \right)\sin \left( \theta \right)\le \frac{1}{2}\theta \le \frac{1}{2}\tan \left( \theta \right)

From this inequality you determine that \displaystyle \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \left( \theta \right)}{\theta }=1

The middle term of the inequality is the area of a sector of a unit circle with central angles of \theta radians. If you work in degrees, this sector’s area is \displaystyle \frac{\pi }{360}\theta  and you will find that \displaystyle \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \left( \theta \right)}{\theta }=\frac{\pi }{180}.

This limit is used to find the derivative of the sin(x). Thus, with x in degrees, \displaystyle \frac{d}{dx}\sin \left( x \right)=\frac{\pi }{180}\cos \left( x \right). This means that with the derivative or antiderivative of any trigonometric function that \displaystyle \frac{\pi }{180} is there getting in the way.

Who needs that?

Do your calculus in radians.

Revision December 7, 2014: The inequality above is derived this way. Consider the unit circle shown below.

unit circle

1. The central angle is \theta  and the coordinates of A are \left( \cos (\theta ),\sin (\theta ) \right).

Then the area of triangle OAB is \frac{1}{2}\cos \left( \theta\right)\sin \left( \theta\right)

2. The area of sector OAD=\frac{\theta}{2\pi }\pi {{\left( 1 \right)}^{2}}=\frac{1}{2}\theta . The sector’s area is larger than the area of triangle OAB.

3. By similar triangles \displaystyle \frac{AB}{OB}=\frac{\sin \left( \theta\right)}{\cos \left( \theta\right)}=\tan \left( \theta\right)=\frac{CD}{1}=CD.

Then the area of \Delta OCD=\frac{1}{2}CD\cdot OD=\frac{1}{2}\tan \left( \theta \right) This is larger than the area of the sector, which establishes the inequality above.

Multiply the inequality by \displaystyle \frac{2}{\sin \left( \theta \right)} and take the reciprocal to obtain \displaystyle \frac{1}{\cos \left( \theta \right)}\ge \frac{\sin \left( \theta \right)}{\theta }\ge \cos \left( \theta \right).

Finally, take the limit of these expression as \theta \to 0 and the limit \displaystyle \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \left( \theta \right)}{\theta }=1 is established by the squeeze theorem.

Fun with Continuity

Posted on by
Reply

Most functions we see in calculus are continuous everywhere or at all but a few points that can be easily identified. But consider the Dirichlet function:

Q\left( x \right)=\left\{ \begin{matrix} 1 & x\in \ rational\ numbers \\ 0 & x\in \ irrational\ numbers \\ \end{matrix} \right.

Since there is one (actually many) rational numbers between any two irrational number and one (many again) irrational numbers between any two rational numbers, this function is not continuous anywhere!

But a very similar function is continuous at exactly one point (1, 1):

f\left( x \right)=\left\{ \begin{matrix} 1 & x\in \ rational\ numbers \\ x & x\in \ irrational\ numbers \\ \end{matrix} \right.

Can you use this idea to make a function that is continuous at exactly two points?

Asymptotes

Posted on by
Reply

Horizontal asymptotes are the graphical manifestation of limits as x approaches infinity. Vertical asymptotes are the graphical manifestation of limits equal to infinity (at a finite x-value).

Thus, since \displaystyle \underset{x\to \infty }{\mathop{\lim }}\,\left( 1-{{2}^{-x}} \right)=1. The graph will show a horizontal asymptote at y = 1.

Since the graph of \displaystyle y={{2}^{-x}}\sin \left( x \right) approaches the x-axis as an asymptote, it follows that \underset{x\to \infty }{\mathop{\lim }}\,\left( {{2}^{-x}}\sin \left( x \right) \right)=0. (The fact that this graph crosses the x-axis many times on its trip to infinity is not a concern; the axis is still an asymptote.)

Since \underset{x\to 0}{\mathop{\lim }}\,\frac{1}{{{x}^{2}}}=\infty ,\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{1}{x}=-\infty ,\text{ and }\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{1}{x}=\infty , the functions all have a vertical asymptote of x = 0.

 

 

 

 

Continuity

Posted on by
1

Limits logically come before continuity since the definition of continuity requires using limits. But practically and historically, continuity comes first. The concept of a limit is used to explain the various kinds of discontinuities and asymptotes. Start by studying discontinuities.

Types of discontinuities to consider: removable (a gap or hole in the graph), jump, infinite (vertical asymptotes), oscillating, and end behavior (horizontal asymptotes).

Numerically: Make a table for the value of \displaystyle \frac{1}{x-3} near x = 3 and as \displaystyle x\to \pm \infty . Relate the values and their signs to the graph. (Divide by a small number get a big number; divide by a big number, get a small number.)

Use the vocabulary of limits to explain the features of graphs. Example: The function \displaystyle \frac{{{x}^{2}}-4}{x-2} has no value at x = 2 (f(2) does not exist), but as you get closer to x = 2 the function value gets closer to 4 (\displaystyle \underset{x\to 2}{\mathop{\lim }}\,f\left( x \right)=4).

Relate the limit, value and graph of the function. In the example above, the graph looks like the line y=x+2 with a gap or hole at the point (2, 4). Another example: \displaystyle \underset{x\to \infty }{\mathop{\lim }}\,\frac{3{{x}^{2}}+x+8}{{{x}^{2}}+1}=3 since, the graph gets closer to y = 3 as you go farther to the right. The line y = 3 is a horizontal asymptote.

Do this numerically as well:  \displaystyle \frac{3{{x}^{2}}+x+8}{{{x}^{2}}+1}=3+\frac{x+5}{{{x}^{2}}+1} and since the fraction gets smaller as |x| gets larger, the function approaches 3 from above when x > 0 and from below when x < 0 (why?)

Extra for your experts: Discuss the reason for the jump discontinuity of

\displaystyle f\left( x \right)=\frac{\cos \left( x \right)\sqrt{{{x}^{2}}-2x+1}}{x-1}