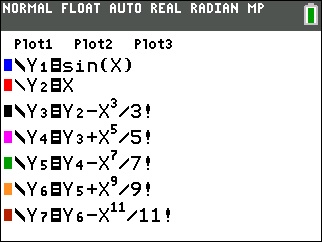
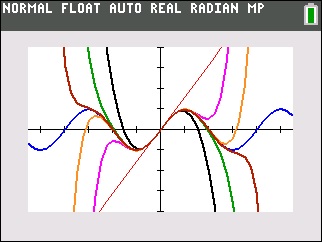
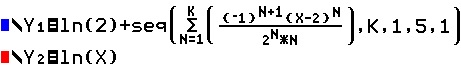Tag Archives: interval of convergence

Why Power Series?

Posted on by
Reply

The polynomial function \displaystyle f\left( x \right)=x-\tfrac{1}{6}{{x}^{3}}+\tfrac{1}{{120}}{{x}^{5}}  approximates the value of \displaystyle \sin \left( {\tfrac{\pi }{6}} \right)correct to 5 decimal places:

\displaystyle f\left( {\tfrac{\pi }{6}} \right)\approx 0.500002

\displaystyle \sin \left( {\tfrac{\pi }{6}} \right)=0.5

This is not a fluke!

The graph of f(x) is in blue, the sin(x) in red. Note how close the two graphs are in the interval [-2, 2]

Now, approximating the value of a sine function is easier with a calculator. But sines are not the only functions in Math World.

In the Unit 10 you will learn how to write special polynomial functions, called Taylor and Maclaurin polynomials, to approximate any differentiable function you want to as many decimal places as you need. You already know a lot about polynomials. They are easy to understand, evaluate, and graph. The concept of using a polynomial to approximate much more complicated functions is very powerful.

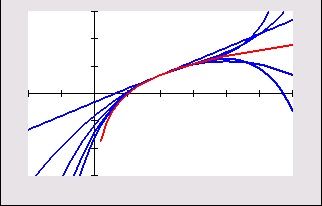
You’ve already got a start on this! Recall that the local linear approximation of a function near x = a is \displaystyle f\left( x \right)\approx f\left( a \right)+{f}'\left( a \right)\left( {x-a} \right). This is a Taylor Polynomial. And it is the first two terms all the higher degree Taylor polynomial for f near x = a.

To fully understand these polynomials, there is a fair amount of preliminary stuff you need to understand. First you study sequences – functions whose domains are whole numbers. Next comes infinite series. A series is written by adding the terms of a sequence. (Sequences and series may have a finite or infinite number of terms. There is not much to say about finite series; infinite sequences and infinite series are where the action is.) oThe terms 0f some sequences and series are numbers. Other series have powers of an independent variable; these are called power series.   

Some power series approximate (converge to) the related function everywhere (i. e. for all Real numbers). Others provide a good approximation only on an interval of finite length. The intervals where the approximation is good is called the interval of convergence. Convergence tests – theorems really – help you determine if a series converges. These in tern help you find the interval of convergence. More on this in my next post.

Depending on your textbook and your teacher, you may study these topics in this order: sequences, convergence test, series, Taylor and Maclaurin polynimials for approximations, and power series. Others may change the order. The path may be different, but the destination will be the same.

Course and Exam Description Unit 10, Sections 10.1, 10.2, 10.11, 10.13, 10.14, 10.15. This is a BC only topic.  

Unit 10 – Infinite Sequences and Series

Posted on by
Reply

Unit 10 covers sequences and series. These are BC only topics (CED – 2019 p. 177 – 197). These topics account for about 17 – 18% of questions on the BC exam.

Topic 10.1: Defining Convergent and Divergent Series.

Topic 10. 2: Working with Geometric Series. Including the formula for the sum of a convergent geometric series.

Topics 10.3 – 10.9 Convergence Tests

The tests listed below are assessed on the BC Calculus exam. Other methods are not tested. However, teachers may include additional methods.

Topic 10.3: The nth Term Test for Divergence.

Topic 10.4: Integral Test for Convergence. See Good Question 14

Topic 10.5: Harmonic Series and p-Series. Harmonic series and alternating harmonic series, p-series.

Topic 10.6: Comparison Tests for Convergence. Comparison test and the Limit Comparison Test

Topic 10.7: Alternating Series Test for Convergence.

Topic 10.8: Ratio Test for Convergence.

Topic 10.9: Determining Absolute and Conditional Convergence. Absolute convergence implies conditional convergence.

Topics 10.10 – 10.12 Taylor Series and Error Bounds

Topic 10.10: Alternating Series Error Bound.

Topic 10.11: Finding Taylor Polynomial Approximations of a Function.

Topic 10.12: Lagrange Error Bound.

Topics 10.13 – 10.15 Power Series

Topic 10.13: Radius and Interval of Convergence of a Power Series. The Ratio Test is used almost exclusively to find the radius of convergence. Term-by-term differentiation and integration of a power series gives a series with the same center and radius of convergence. The interval may be different at the endpoints.

Topic 10.14: Finding the Taylor and Maclaurin Series of a Function. Students should memorize the Maclaurin series for \displaystyle \frac{1}{{1-x}}, sin(x), cos(x), and ex.

Topic 10.15: Representing Functions as Power Series. Finding the power series of a function by differentiation, integration, algebraic processes, substitution, or properties of geometric series.

Timing

The suggested time for Unit 9 is about 17 – 18 BC classes of 40 – 50-minutes, this includes time for testing etc.

Previous posts on these topics:

Before sequences

Amortization Using finite series to find your mortgage payment. (Suitable for pre-calculus as well as calculus)

A Lesson on Sequences.  An investigation, which could be used as early as Algebra 1, showing how irrational numbers are the limit of a sequence of approximations. Also, an introduction to the Completeness Axiom. 

Everyday Series

Convergence Tests

Reference Chart

Which Convergence Test Should I Use? Part 1: Pretty much anyone you want!

Which Convergence Test Should I Use? Part 2: Specific hints and a discussion of the usefulness of absolute convergence

Good Question 14 on the Integral Test

Sequences and Series

Graphing Taylor Polynomials.  Graphing calculator hints

Introducing Power Series 1

Introducing Power Series 2

Introducing Power Series 3

New Series from Old 1: Substitution (Be sure to look at example 3)

New Series from Old 2: Differentiation

New Series from Old 3: Series for rational functions using long division and geometric series

Geometric Series – Far Out: An instructive “mistake.”

A Curiosity: An unusual Maclaurin Series

Synthetic Summer Fun Synthetic division and calculus including finding the (finite)Taylor series of a polynomial.

Adapting 2021 BC 5

Adapting 2021 BC 6

Error Bounds

Error Bounds: Error bounds in general and the alternating Series error bound, and the Lagrange error bound

The Lagrange Highway: The Lagrange error bound. 

What’s the “Best” Error Bound?

Review Notes

Type 10: Sequences and Series Questions

Infinite Sequences and Series – Unit 10

Posted on by
Reply

Unit 10 covers sequences and series. These are BC only topics (CED – 2019 p. 177 – 197). These topics account for about 17 – 18% of questions on the BC exam.

Topics 10.1 – 10.2

Topic 10.1: Defining Convergent and Divergent Series.

Topic 10. 2: Working with Geometric Series. Including the formula for the sum of a convergent geometric series.

Topics 10.3 – 10.9 Convergence Tests

The tests listed below are tested on the BC Calculus exam. Other methods are not tested. However, teachers may include additional methods.

Topic 10.3: The nth Term Test for Divergence.

Topic 10.4: Integral Test for Convergence. See Good Question 14

Topic 10.5: Harmonic Series and p-Series. Harmonic series and alternating harmonic series, p-series.

Topic 10.6: Comparison Tests for Convergence. Comparison test and the Limit Comparison Test

Topic 10.7: Alternating Series Test for Convergence.

Topic 10.8: Ratio Test for Convergence.

Topic 10.9: Determining Absolute and Conditional Convergence. Absolute convergence implies conditional convergence.

Topics 10.10 – 10.12 Taylor Series and Error Bounds

Topic 10.10: Alternating Series Error Bound.

Topic 10.11: Finding Taylor Polynomial Approximations of a Function.

Topic 10.12: Lagrange Error Bound.

Topics 10.13 – 10.15 Power Series

Topic 10.13: Radius and Interval of Convergence of a Power Series. The Ratio Test is used almost exclusively to find the radius of convergence. Term-by-term differentiation and integration of a power series gives a series with the same center and radius of convergence. The interval may be different at the endpoints.

Topic 10.14: Finding the Taylor and Maclaurin Series of a Function. Students should memorize the Maclaurin series for \displaystyle \frac{1}{{1-x}}, sin(x), cos(x), and ex.

Topic 10.15: Representing Functions as Power Series. Finding the power series of a function by, differentiation, integration, algebraic processes, substitution, or properties of geometric series.

Timing

The suggested time for Unit 9 is about 17 – 18 BC classes of 40 – 50-minutes, this includes time for testing etc.

Previous posts on these topics:

Before sequences

Amortization Using finite series to find your mortgage payment. (Suitable for pre-calculus as well as calculus)

A Lesson on Sequences An investigation, which could be used as early as Algebra 1, showing how irrational numbers are the limit of a sequence of approximations. Also, an introduction to the Completeness Axiom. 

Everyday Series

Convergence Tests

Reference Chart

Which Convergence Test Should I Use? Part 1 Pretty much anyone you want!

Which Convergence Test Should I Use? Part 2 Specific hints and a discussion of the usefulness of absolute convergence

Good Question 14 on the Integral Test

Sequences and Series

Graphing Taylor Polynomials Graphing calculator hints

Introducing Power Series 1

Introducing Power Series 2

Introducing Power Series 3

New Series from Old 1 substitution (Be sure to look at example 3)

New Series from Old 2 Differentiation

New Series from Old 3 Series for rational functions using long division and geometric series

Geometric Series – Far Out An instructive “mistake.”

A Curiosity An unusual Maclaurin Series

Synthetic Summer Fun Synthetic division and calculus including finding the (finite)Taylor series of a polynomial.

Error Bounds

Error Bounds Error bounds in general and the alternating Series error bound, and the Lagrange error bound

The Lagrange Highway The Lagrange error bound. 

What’s the “Best” Error Bound?

Review Notes

Type 10: Sequences and Series Questions

 

 

 

 

 

2019 CED Unit 10: Infinite Sequences and Series

Posted on by
Reply

Unit 10 covers sequences and series. These are BC only topics (CED – 2019 p. 177 – 197). These topics account for about 17 – 18% of questions on the BC exam.

Topics 10.1 – 10.2

Timing

The suggested time for Unit 9 is about 17 – 18 BC classes of 40 – 50-minutes, this includes time for testing etc.

Previous posts on these topics :

Introducing Power Series 1

Geometric Series – Far Out

Posted on by
1

One of the great things – at least I like it – about the Taylor series of a function is that it is unique. There is only one Taylor series for any function centered at a given point, what that means is that any way you get it, it’s right.

Faced with writing the power series for, say, \displaystyle f\left( x \right)=\frac{3x}{1-2x}, instead of cranking out a bunch of derivatives, we can say this looks a lot like the formula for the sum of a geometric series,

\displaystyle \sum\limits_{k=1}^{\infty }{a{{r}^{k-1}}}=\frac{a}{1-r}. Taking  a = 3x and r = 2x, the series is

\displaystyle \frac{3x}{1-2x}=3x+6{{x}^{2}}+12{{x}^{3}}+24{{x}^{4}}+\cdots =3\cdot \sum\limits_{k=1}^{\infty }{{{2}^{k-1}}{{x}^{k}}}.

Furthermore, since a geometric series converges only when \left| r \right|<1, the interval of convergence for this series is \left| 2x \right|<1 or -\tfrac{1}{2}<x<\tfrac{1}{2} and we don’t even have to check the endpoints.

There are other choices as well.  We could write \displaystyle f\left( x \right)=3x{{\left( 1-2x \right)}^{-1}} and then expand the binomial using the binomial theorem. Or we could use the technique of long division of polynomials to divide 3x by (1 – 2x) – leaving the divisor as written here.

This works even in more complicated situations. Let \displaystyle g\left( x \right)=\frac{3x}{{{x}^{2}}-4}. Begin by dividing each term by –4. This gives \displaystyle g\left( x \right)=\frac{-\tfrac{3}{4}x}{1-\tfrac{1}{4}{{x}^{2}}}. Then treating this as a geometric series

\displaystyle g\left( x \right)=\sum\limits_{k=1}^{\infty }{-\tfrac{3}{4}x{{\left( \tfrac{1}{4}{{x}^{2}} \right)}^{k-1}}=-\frac{3}{4}x-\frac{3}{16}{{x}^{3}}-\frac{3}{64}{{x}^{5}}-\frac{3}{256}{{x}^{7}}-\cdots }

The interval of convergence is \displaystyle \left| \tfrac{1}{4}{{x}^{2}} \right|<1, or –2 < x < 2

Now the fun part

I once heard of a student making one of those great “mistakes.” For the series above, she divided by (–x2) and found that \displaystyle g\left( x \right)=\frac{-\frac{3}{x}}{1-\frac{4}{{{x}^{2}}}} and then wrote:

\displaystyle g\left( x \right)=\sum\limits_{k=1}^{\infty }{\left( -\frac{3}{x} \right){{\left( \frac{4}{{{x}^{2}}} \right)}^{k-1}}=-\frac{3}{x}-\frac{12}{{{x}^{3}}}-\frac{48}{{{x}^{5}}}-\frac{192}{{{x}^{7}}}-\cdots }

So, what’s wrong with that?

Nothing actually.

Okay, it’s not a Taylor Series since a Taylor series is allowed only non-negative exponents, but it’s still a geometric series. Let’s take a look at its interval of convergence: \displaystyle \left| \frac{4}{{{x}^{2}}} \right|<1, or \displaystyle \left| \frac{{{x}^{2}}}{4} \right|>1,  or the union of x>2 and x<-2, Whoa, that’s different and not even an interval.

The graph will make things clear (as usual):

geom-series

The original function graphed as a rational expression is shown in black. The Taylor polynomial (4 terms) is shown in blue; it approximates the function well between –2 and 2 as we should expect. The red graph is the student’s series (4 terms) and it is a good approximation of the series outside of the interval (–2, 2), far outside! Way Cool!

Of course, this kind of series is not studied in beginning calculus. It may make a good topic for a report or project for someone in your class.

Graphing Taylor Polynomials

Posted on by
Reply

The eighth in the Graphing Calculator / Technology series

Here are some hints for graphing Taylor polynomials using technology. (The illustrations are made using a TI-8x calculator. The ideas are the same on other graphing calculators; the syntax may be slightly different.)

Each successive term of a Taylor polynomial consists of all the previous terms plus one new term. To show students how Taylor polynomials closely approximate a function (in the interval of convergence, of course), enter the function as Y1. Then enter the first term of the polynomial as Y2. Enter the next polynomial as Y3 = Y2 + the second term; enter the next as y4 = Y3 + the next term, and so on.

The example is the McLaurin series for sin(x) centered at the origin:

\displaystyle \sin \left( x \right)=x-\frac{{{x}^{3}}}{3!}+\frac{{{x}^{5}}}{5!}+\cdots +\frac{{{(-1)}^{2n-1}}{{x}^{2n-1}}}{\left( 2n-1 \right)!}=\sum\limits_{n=1}^{\infty }{{{\left( -1 \right)}^{n+1}}\frac{{{x}^{2n-1}}}{\left( 2n-1 \right)!}}

Each will graph one at a time. Watching them graph, one at a time, is instructive as well; each curve approximates the sine curve (in black) further and further away from the origin.

series-1

series-2

Another way to graph the polynomials is to enter them as a sequence of sums. The example this time is ln(x) centered at x = 2:

\displaystyle \ln \left( x \right)=\ln \left( 2 \right)+\frac{x-2}{2}-\frac{{{\left( x-2 \right)}^{2}}}{8}+\frac{{{\left( x-2 \right)}^{3}}}{24}+...=\ln \left( 2 \right)+\sum\limits_{n=1}^{\infty }{{{\left( -1 \right)}^{n+1}}\frac{{{\left( x-2 \right)}^{n}}}{{{2}^{n}}n}}

The syntax is seq( series in sigma notation, indexing variable, start value, end value [,step]). Notice from the figure that the indexing variable, K, is above the sigma.

series-4

The individual polynomials graph in the same color (blue); the function is shown in red.

series-3Comparing the two graphs (sin(x) and ln(x)) is a good way to start a discussion about the interval of convergence – ask what is different about the graphs as more polynomials are graphed on each. Notice that unlike the sin(x) series the ln(x) polynomials only come close to the function in a limited interval (0, 4) centered at x = 2.

Desmos is also a good program to use to illustrate Taylor and McLaurin polynomials (as are Geogebra and Winplot). The use of the sliders makes it possible to see the successive polynomials quickly. They also help students see the interval of convergence as higher degree polynomials hug the graph on wider intervals (sin(x)), or stay within the same interval (ln(x)). The Desmos illustration with slider for the sin(x) centered at the origin is here and for ln(x)  centered at x = 2 is here. Study the input on the left side and enter Taylor polynomials for other functions.

The fifth degree Taylor polynomial for sin(x) centered at the origin.The interval of convergence is all real numbers. Each polynomial “hugs” the graph on wider intervals.

The fifth degree Taylor polynomial for ln(x) centered at x = 2. The interval of convergence is 0 < x < 4. The polynomials all leave the graph outside of this interval.

Coming soon

Feb 14th, Geometric Series – Far Out