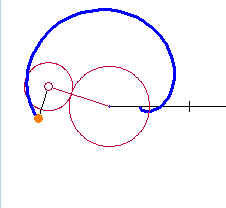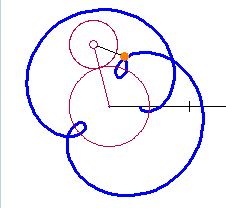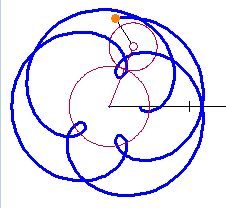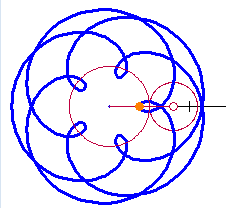
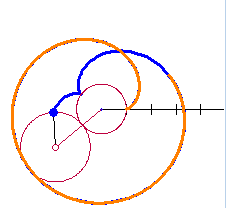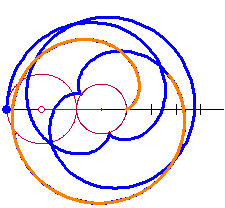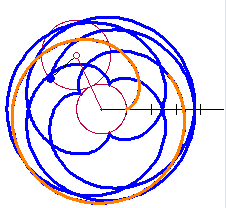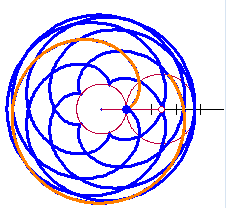
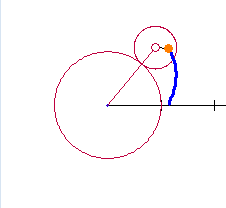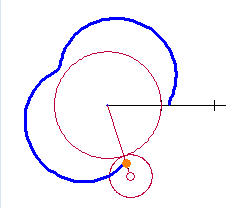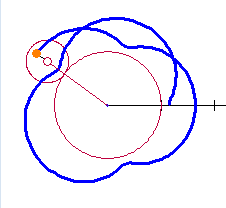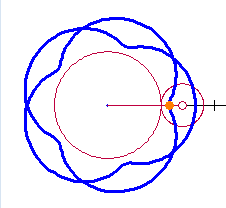Epitrochoids

Posted on July 1, 2014 by Lin McMullin

Roulettes – 3: Epitrochoids

In the first post of this series Roulette Generators are explained. Here are the files for Winplot or Geometer’s Sketchpad. Use them to quickly see the graphs of these curves by adjusting one or two parameters.

The parametric equations of these curves are below. R and S are parameters that are adjusted for each curve.

$x\left( t \right)=(1+R)\cos \left( t \right)-S\cos \left( \tfrac{1}{R}t+t \right)$

$y\left( t \right)=\left( 1+R \right)\sin \left( t \right)-S\sin \left( \tfrac{1}{R}t+t \right)$

Before looking at Epitrochoids, consider the three kinds of cycloids. A cycloid is the locus of a point attached to a circle rolling along a line.If the point is on the circle a cycloid is generated.

Cycloid – A point on a circle rolling on a line.

If the point is in the interior of the circle a curtate cycloid is generated.

Curtate Cycloid. A point in the interior of a circle rolling on a line.

If the point is in the exterior of the circle a prolate cycloid is generated.

Prolate Cycloid. A point attached outside a circle (such as on the flange of a train wheel) rolling on a line.

Using our Roulette Generator we can produce similar curves called epitrochoids the locus of a point attached to one circle as it rolls around another circle. If the point is on the moving circle an epicycloid is generated. These were discussed in the preceding post. R is the radius of the moving circle and S is the distance of the point whose locus is graphed from the center of the moving circle.

R = S = 1/3

By changing the position of the point relative to the center (where S = 0) we can see a similarity with the cycloids.

If the point is in the interior of the moving circle (S < R), then the curves look like this:

R = 0.4 and S = 0.25. $0\le t\le 4\pi$

A close inspection will show that this curve is similar to the curtate cycloid wrapped around a circle.

The next obvious question is what happens if S > R? Then the resulting curves have inner loops similar to those of the prolate cycloid.

S = 0.84, R = 0.6 $0\le t\le 6\pi$

Finally, we can see the range of curves by changing the values of S. The next video shows the progression of shapes as S changes from 4 to -4 . Watch the orange point. S is the distance between the orange point and the center of the smaller moving circle(open point). The negative values amount to starting the moving circle on the opposite side of the fixed circle and gives the same curves in a different orientation.

$R=0.6,\,t=6\pi ,\,-4\le S\le 4$

Investigation 5: What is the shape of the curve when S = 0?

Investigation 6: What shape does the curve approach as S approaches infinity?

Next post: hypocycloid – for those who like to be negative.

References:

Cycloid: http://en.wikipedia.org/wiki/Cycloid

Epitrochoids: http://en.wikipedia.org/wiki/Epitrochoid

Epicycloids

Posted on June 27, 2014 by Lin McMullin

Roulettes – 2: Epicycloids

In the last post we saw how a cardioid can be generated by watching the locus of a point on as one circle rolls around another circle with the same radius. In the first post of this series Roulette Generators are explained. Here are the files for Winplot or Geometer’s Sketchpad. Use them to quickly see the graphs of these curves by adjusting one or two parameters.

The parametric equations of these curves are below. R and S are parameters that are adjusted for each curve.

$x\left( t \right)=(1+R)\cos \left( t \right)-S\cos \left( \tfrac{1}{R}t+t \right)$

$y\left( t \right)=\left( 1+R \right)\sin \left( t \right)-S\sin \left( \tfrac{1}{R}t+t \right)$

A cardioid, a type of cycloid $R=S=1;\quad 0\le t\le 2\pi$

If the circles have the same radii and therefore the same circumferences, as the moving circle rolls around the fixed circle once, the point traces a path called a cardioid, and returns to its original orientation.

Let’s see what happens if we make the moving circle smaller. Make R= S = ½. Now the radius of the moving circle is one-half the radius of the fixed circle. The circumference is also half the circumference of the fixed circle. The smaller circle makes two rotations in going once around the larger circle before returning to the initial orientation.

Epicycloid R = S = 0.5 $R=S=0.5\quad 0\le t\le 2\pi$

Now try other values keeping R = S. Make their values unit fractions, 1/n where n is a positive integer. (Note that $\tfrac{1}{R}=n$ .) Here are some examples:

: Epicycloid R = S = 1/3

: Epicycloid R = S = 1/4

: Epicycloid R = S = 1/10

For R = S = 1/n there are n sections of the graph as t goes from 0 to $2\pi$ . The places where the cycles end are evenly spaced around the fixed circle and the locus has a cusp at these places.

What if we use other rational numbers? All of a sudden things are very different:

$R=S=\tfrac{2}{3}\text{, }0\le t\le 2\pi$

Now the circumference of the larger circle is not a multiple of the circumference of the smaller. To return the circle to its starting orientation we have to go around once more by letting t go from 0 to $4\pi$ . The first time around (from 0 to $2\pi$ ) is shown in orange and the rest of the path in blue.

$R=S=\tfrac{2}{3},\quad 0\le t\le 4\pi$

Investigation 1: Using the ratio of the radius of the fixed circle to the moving circle, determine how many times the moving circle must go around the fixed circle to draw a complete curve.

If $R=\frac{n}{d}$ is a rational number (reduced), then by increasing the maximum value of t to $2n\pi$ the moving circle will return to its original position after n revolutions and after that the curve will be retraced. This is the same regardless of whether $\tfrac{n}{d}$ is greater than or less than 1.

We now turn our attention to the cusps; the places where the point “bounces off” the fixed circle.

Investigation 2: Using the ratio of the radius of the fixed circle to the moving circle, determine how many cusps the graph will have.

For these curves, If $R=\frac{n}{d}$ there are d places where the locus “bounces” of the fixed circle. These appear as cusps of the locus.

$R=S=\tfrac{7}{5}\text{, }0\le t\le 14\pi$

Finally, if R is not rational, the moving circle will never return to its original orientation and the locus will keep adding cusps as the circle continues to roll round the fixed circle

$R=S=\sqrt{2},\quad 0\le t\le 100$

Curves of this type, with the moving circle smaller or larger than the fixed circle and R = S, are called epicycloids. Epicycloids are a special case of Epitrochoids which will be the subject of the next post in this series.

Investigation 3: Determine the value of t for each cusp, of a graph with d cusps.

Solution left as an exercise.

Investigation 4: Investigate the derivative at a cusp.

Solution left as an exercise. This will be discussed in a later post.

References:

Cardioids: http://en.wikipedia.org/wiki/Cardioid

Epicycloids: http://en.wikipedia.org/wiki/Epicycloid

Epitrochoids: http://en.wikipedia.org/wiki/Epitrochoid

Corrections made July 5, 2014

Rolling Circles

Posted on June 24, 2014 by Lin McMullin

A few weeks ago I covered some trigonometry classes for another teacher. They were studying polar and parametric graphs and the common curves limaçon, rose curves, cardioids, etc. I got to thinking about these curves. the next few posts will discuss what I learned. To help me see what was happening I made a Winplot animation. My “Roulette Generator” (RG) is a rather simple setup and turned out to be very well suited to study a variety of curves: cardioids, epicycloids, epitrochoids, hypochoids, and hypotrochoids to name a few. They are all examples of roulettes – curves generated by a point on a curve as it moves around anther curve. I considered only cases where both curves are circles. Calculus will make it appearance after the first few posts in this series. I hope you will find information here that will let you make a good project or investigation for calculus or precalculus students. The RG can be set to graph any number of situations as I will discuss. So here goes.

Roulettes – 1: Equations and the Roulette Generator.

In this post I will discuss the derivation of the parametric equations used to make the animations and some notes on how to use the RG. Later posts will discuss some of the various curves that result. I began with a simple cardioid.

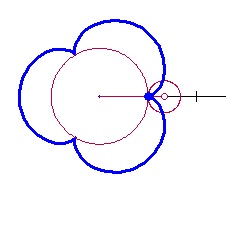
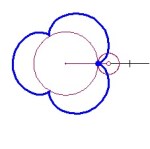
Cardioid R = S = 1

A cardioid is defined as the locus of a point on a circle as it rolls without slipping around another circle with the same radius.

The setup described here will allow us to change the equations using sliders, for this and a number of related curves. The two circles with the same radii are shown in the figure below. The circle with center at C rolls counterclockwise around the circle with center at the origin, O. The point D traces the cardioid. The blue curve from F to D is the beginning of the cardioid. The equations of the circles are: The circle centered at the origin with radius 1:

$x\left( t \right)=\cos \left( t \right)\text{ and }y\left( t \right)=\sin \left( t \right)$

The moving circle with center at C and radius R:

$x\left( t \right)=(1+R)\cos (t)+R\cos (t)$ and

$y\left( t \right)=(1+R)\sin \left( t \right)+R\sin \left( t \right)$ .

The equation of the locus: In the figure above, the locus of the point marked D, as the moving circle rolls counterclockwise around the fixed circle, will be the path of the curves. A small portion of the curve is shown in blue running from F to D. In our investigations we will eventually want to place the moving point inside, on, or outside the moving circle. To do this we will use S as the distance from the center of the moving circle to the point we are watching. For the moment and for the simple cardioid, we will assume they are the same: $R=S=1$ .

The ratio of the radius of the fixed circle to the radius of the moving circle is 1/R, and will be of interest. The ratio can be adjusted by changing R. We can, therefore, keep the fixed circle’s radius constant and equal to one.

We will use vectors to write the locus. Before writing the individual vectors consider first that the arc length on both circles is always the same for all the curves and combinations of their radii:

$\text{arc }EF=t=\text{arc }DE=R\left( \measuredangle DCE \right)$ .

Therefore, $\measuredangle DCE=\tfrac{1}{R}t$ . Then $\measuredangle BCD=\tfrac{\pi }{2}-\left( \tfrac{1}{R}t+t \right)$ Then the locus of D has the vector equation:

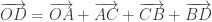
$\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{BD}$

$\overrightarrow{OD}=\left\langle (1+R)\cos (t),0 \right\rangle +\left\langle 0,\left( 1+R \right)\sin \left( t \right) \right\rangle +$

$\left\langle -S\sin \left( \tfrac{\pi }{2}-(\tfrac{1}{R}t+t) \right),0 \right\rangle +\left\langle 0,-S\cos \left( \tfrac{\pi }{2}-(\tfrac{1}{R}t+t) \right) \right\rangle$

Notice that $\left( \tfrac{1}{R}t+t \right)$ is the complement of $\left( \tfrac{\pi }{2}-\left( \tfrac{1}{R}t+t \right) \right)$ , so that $\sin \left( \tfrac{\pi }{2}-(\tfrac{1}{R}t+t) \right)=\cos \left( \tfrac{1}{R}t+t \right)$ and $\cos \left( \tfrac{\pi }{2}-(\tfrac{1}{R}t+t) \right)=\sin \left( \tfrac{1}{R}t+t \right)$ . The parametric equations of the path are

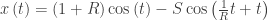
$x\left( t \right)=(1+R)\cos \left( t \right)-S\cos \left( \tfrac{1}{R}t+t \right)$

$y\left( t \right)=\left( 1+R \right)\sin \left( t \right)-S\sin \left( \tfrac{1}{R}t+t \right)$

You may enter these equations on any graphing calculator by entering specific values of R and S. You will have to re-type them for each different curve. With the RG you can make the changes easily with sliders.

The roulette generators: I used Winplot a free graphing program I’ve used for years. Here are the links so you can download Winplot or Winplot for Macs. the Winplot file containing the generator is here: Winplot Roulette Generator. [Sorry, this is no longer available here and WordPress will not accept Winplot files for download. Please contact me at lnmcmullin@aol.com and I’ll send you a copy.] The Winplot equations are discussed here: Notes on the Roulette Generator.

A Geometer’s Sketchpad version may be downloaded Geometer’s Sketchpad Roulette Generator. You will need Geometer’s Sketchpad to run this on a computer or the “Sketch Explorer” app for iPads and other tablets. A big ‘Thanks” to Audrey Weeks who was kind enough to make this for us. Audrey is the author of the Algebra in Motion and Calculus in Motion software. Audrey is my “go to” person when I have math questions.

Other graphers with sliders such as Geogebra and TI-Nspire will probably work as well. For those who wish to adapt this to some other graphing program there are some syntax consideration to making the one circle roll around the other and showing the path as the circle rolls. If you make your own generator on one of these other platforms, please send it along and I’ll post it and give you credit.

Experiment with the R and S sliders. In the next several posts well will do this and learn about various other curves.

Next: Epicycloids

References:

Cardioids: http://en.wikipedia.org/wiki/Cardioid

Roulettes: http://en.wikipedia.org/wiki/Roulette_(curve)

Algebra in Motion

Calculus in Motion

New Look

Posted on June 20, 2014 by Lin McMullin

I am back from my sojourn in Hawai’i. It was a great year. I enjoyed being back in the classroom and working with the kids. My wife and I had a whale of a good time. I decided to freshen up the look of the blog with a new format. I have some new post coming in a few days. Meanwhile – or maybe after your vacation – please continue to use the blog. I’ve had over 100,000 hits so far. If you find it helpful, please tell your friends and students (whom I hope are also your friends) about it.

As always, I appreciate your input. Please ask questions and click the “Like” button. I would especially like to know if there is any topic or concept you would like me to discuss or expand on. In the column on the right are various ways of finding what you are looking for. Use the search box or the Posts by Topic list to get started.

A Problem with 4 Solutions and 2 Morals

Posted on June 6, 2014 by Lin McMullin

A friend of mine e-mailed me yesterday with a question: Her class was using the Law of Cosines and came up with a solution of $\sqrt{8-4\sqrt{3}}$ , but the “correct” answer was $\sqrt{2}\left( \sqrt{3}-1 \right)$ . She wanted to know, having gotten the first answer, how do you get to the second from it. The answers are equivalent: I figured it out this way

$\sqrt{8-4\sqrt{3}}=\sqrt{6-4\sqrt{3}+2}=\sqrt{{{\left( \sqrt{6}-\sqrt{2} \right)}^{2}}}=\left| \sqrt{6}-\sqrt{2} \right|=\sqrt{2}\left( \sqrt{3}-1 \right)$

But in fact, I had worked that from the second back to the first. So I sent the problem to another friend who sent this back: This is a more formal way of what I did. (The solution k = 6 gives the same expression.) But the real question is how is a student supposed to know any of this? My friend wrote, “This problem seems really complicated for multiple=choice. Remember that this is what we had to do AFTER we had done law of cosines to get to that first step.” I agree. Then I asked her for the original problem, which is what I should have done in the first place. The original problem was to find the base of an isosceles triangle with a vertex angle of 30^o and congruent sides of 2. Well that’s a whole different story: $x=2\cos \left( 75 \right)=2\cos \left( 45+30 \right)$ $x=2\left( \cos (45)\cos (30)-\sin (45)\sin (30) \right)$ $x=2\left( \left( \frac{\sqrt{2}}{2} \right)\left( \frac{\sqrt{3}}{2} \right)-\left( \frac{\sqrt{2}}{2} \right)\left( \frac{1}{2} \right) \right)$ $Base=2x=\sqrt{6}-\sqrt{2}$ And also $x=2\sin \left( 15 \right)=2\sin \left( 45-30 \right)$ works the same way. But there is yet another way: we could draw a different perpendicular and get a 30-60-90 triangle (not to scale): Then using the Pythagorean Theorem on the lower triangle: $base=\sqrt{{{\left( 2-\sqrt{3} \right)}^{2}}+{{1}^{2}}}=\sqrt{\left( 4-4\sqrt{3}+3 \right)+1}=\sqrt{8-4\sqrt{3}}$

The morals of the story:

First as we have all discovered, when a student asks, “What do I do now?” or “How can I get from here to here?” Go back to the original question. Do not jump in the middle and answer the wrong question.

Second, while I am definitely not against multiple-choice problems, this is a horrible multiple-choice question. It is horrible because there are so many good ways to do it, but they lead to different looking answers. Students should not be penalized for doing good mathematics. It is fine to require a student to do a problem by a certain method if you are currently teaching that method. But with no method specified, the students should not get a correct answer and then have to really struggle to get your answer. On the other hand, this is a very good questions, precisely because there are so many ways to do it and because the answers look different.

Implicit Differentiation of Parametric Equations

Posted on May 17, 2014 by Lin McMullin

I’ve never liked memorizing formulas. I would rather know where they came from or be able to tie it to something I already know. One of my least favorite formulas to remember and explain was the formula for the second derivative of a curve given in parametric form. No longer.

If $y=y\left( t \right)$ and, $x=x\left( t \right)$ then the tradition formula gives

$\displaystyle \frac{d}{dx}y\left( t \right)=\frac{dy/dt}{dx/dt}$ , and

$\displaystyle \frac{{{d}^{2}}y}{d{{x}^{2}}}=\frac{\frac{d}{dt}\left( \frac{dy}{dx} \right)}{\frac{dx}{dt}}$

It is that last part, where you divide by $\displaystyle \frac{dx}{dt}$ , that bothers me. Where did the $\displaystyle \frac{dx}{dt}$ come from?

Then it occurred to me that dividing by $\displaystyle \frac{dx}{dt}$ is the same as multiplying by $\displaystyle \frac{dt}{dx}$

It’s just implicit differentiation!

Since $\displaystyle \frac{dy}{dx}$ is a function of t you must begin by differentiating the first derivative with respect to t. Then treating this as a typical Chain Rule situation and multiplying by $\displaystyle \frac{dt}{dx}$ gives the second derivative. (There is a technical requirement here that given $x=x\left( t \right)$ , then $t={{x}^{-1}}\left( x \right)$ exists.)

In fact, if you look at a proof of the formula for the first derivative, that’s what happens there as well:

$\displaystyle \frac{d}{dx}y\left( t \right)=\frac{dy}{dt}\cdot \frac{dt}{dx}=\frac{dy/dt}{dx/dt}$

The reason you to do it this way is that since x is given as a function of t, it may be difficult to solve for t so you can find dt/dx in terms of x. But you don’t have to; just divide by dx/dt which you already know.

Here is an example for both derivatives.

Suppose that $x={{t}^{3}}-3$ and $y=\ln \left( t \right)$

Then $\displaystyle \frac{dy}{dt}=\frac{1}{t}$ , and $\displaystyle \frac{dx}{dt}=3{{t}^{2}}$ and $\displaystyle \frac{dt}{dx}=\frac{1}{3{{t}^{2}}}$ .

Then $\displaystyle \frac{dy}{dx}=\frac{1}{t}\cdot \frac{dt}{dx}=\frac{1}{t}\cdot \frac{1}{3{{t}^{2}}}=\frac{1}{3{{t}^{3}}}=\frac{1}{3}{{t}^{-3}}$

And $\displaystyle \frac{{{d}^{2}}y}{d{{x}^{2}}}=\left( \frac{d}{dt}\left( \frac{dy}{dx} \right) \right)\cdot \frac{dt}{dx}=\left( -{{t}^{-4}} \right)\cdot \frac{dt}{dx}=\left( -{{t}^{-4}} \right)\left( \frac{1}{3{{t}^{2}}} \right)=-\frac{1}{3{{t}^{6}}}$

Yes, it’s the same thing as using the traditional formula, but now I’ll never have to worry about forgetting the formula or being unsure how to explain why you do it this way.

Revised: Correction to last equation 5/18/2014

Revised: 2/8/2016

Percentages Don’t Make the Grade

Posted on May 12, 2014 by Lin McMullin

Well, the AP exams have been written and the dust has settled. Folks are posting their answers on the Community Bulletin Boards. (I never post mine – too many mistakes.) The other thing that always gets discussed at this time of year is whether this year’s exam is more difficult or less difficult than last year’s.

I am sure this year’s was more difficult or less difficult than last year’s because it is impossible to make two exams of the same difficulty.

But it doesn’t matter.

The grades will reflect, as best as possible, that a student knows as much calculus as students with the same score did last year. That’s the important thing.

Because it is impossible for anyone or any group to make two exams of the same difficulty, percentages tell you nothing. The percentage of the number of points that a student earns out of the number possible tells you just that and nothing more. If the tests are not of the exact same difficulty, then percentages are meaningless.

What to do?

The Educational Testing Service (ETS) who writes and administers the AP exams for the College Board carefully pretests each question. Also, there are a number of questions from last year’s exam on this year’s exam. These questions, called equators, allow ETS to judge the difficulty of the other questions on this year’s exam compared to last year’s. It allows them to judge the ability of this year’s student cohort compared to last year’s. Each question is considered individually. Questions that score poorly or questions that identifiable groups of students do far worse compared to the entire group taking the test are not counted in the final score. (For example, in 2008 question AB 19 was not counted; too many missed it.) They compare the results of questions within each exam. With this information they “scale” the exams and decide on the cut points, the high and low raw scores that earn a 5, 4, 3, 2, or 1.

A teacher on a day-to-day basis cannot do so detailed an analysis. Yet we still need to give students grades. We need to scale the exams. I was quite happy this year using a scheme Dan Kennedy suggested some years ago (see resources tab above). This worked quite well for me in BC Calculus and in 8^th grade Algebra 1. Perhaps you have another system.

Percentages just don’t make the grade.

Update September 22, 2014: Matthew Braddock, Mathematics Instructor & Webmaster, at the Dr. Henry A. Wise, Jr., High School in Prince George’s County, Maryland sent me a GeoGebra applet that will calculate the grades using Dan Kennedy’s scheme described in the link above. It runs at a website so you do not need GeoGebra on your computer or iPad to use it. Simply enter the information and it will do the rest. Thank you Matthew.

Update December 3, 2018. The link above is no longer active. This link is to a similar app by Dan Anderson on Desmos. Thank you Dan. For more on this scaling test see the post: On Scaling.

Updated: September 22,2014, Kennedy link fixed February 9, 2018

Teaching Calculus

The pleasure lies not in discovering the truth, but in searching for it.

Author Archives: Lin McMullin

Epitrochoids

Investigation 5: What is the shape of the curve when S = 0?

Investigation 6: What shape does the curve approach as S approaches infinity?

Epicycloids

Investigation 1: Using the ratio of the radius of the fixed circle to the moving circle, determine how many times the moving circle must go around the fixed circle to draw a complete curve.

Investigation 2: Using the ratio of the radius of the fixed circle to the moving circle, determine how many cusps the graph will have.

Investigation 3: Determine the value of t for each cusp, of a graph with d cusps.

Investigation 4: Investigate the derivative at a cusp.

Rolling Circles

New Look

A Problem with 4 Solutions and 2 Morals

Implicit Differentiation of Parametric Equations

Percentages Don’t Make the Grade

Investigation 5: What is the shape of the curve when S = 0?

Investigation 6: What shape does the curve approach as S approaches infinity?

Share this:

Investigation 1: Using the ratio of the radius of the fixed circle to the moving circle, determine how many times the moving circle must go around the fixed circle to draw a complete curve.

Investigation 2: Using the ratio of the radius of the fixed circle to the moving circle, determine how many cusps the graph will have.

Investigation 3: Determine the value of t for each cusp, of a graph with d cusps.

Investigation 4: Investigate the derivative at a cusp.

Share this:

Share this:

Share this:

Share this:

Share this:

Share this: