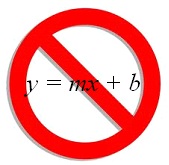Category Archives: Before Calculus

Stamp Out Slope-intercept Form!

Posted on by
8

Accumulation 5: Lines

Ban Slope Intercept

If you have a function y(x), that has a constant derivative, m, and contains the point \left( {{x}_{0}},{{y}_{0}} \right) then, using the accumulation idea I’ve been discussing in my last few posts, its equation is

\displaystyle y={{y}_{0}}+\int_{{{x}_{0}}}^{x}{m\,dt}

\displaystyle y={{y}_{0}}+\left. mt \right|_{{{x}_{0}}}^{x}

\displaystyle y={{y}_{0}}+m\left( x-{{x}_{0}} \right)

This is why I need your help!

I want to ban all use of the slope-intercept form, y = mx + b, as a method for writing the equation of a line!

The reason is that using the point-slope form to write the equation of a line is much more efficient and quicker. Given a point \left( {{x}_{0}},{{y}_{0}} \right) and the slope, m, it is much easier to substitute into  y={{y}_{0}}+m\left( x-{{x}_{0}} \right) at which point you are done; you have an equation of the line.

Algebra 1 books, for some reason that is beyond my understanding, insist using the slope-intercept method. You begin by substituting the slope into y=mx+b and then substituting the coordinates of the point into the resulting equation, and then solving for b, and then writing the equation all over again, this time with only m and b substituted. It’s an algorithm. Okay, it’s short and easy enough to do, but why bother when you can have the equation in one step?

Where else do you learn the special case (slope-intercept) before, long before, you learn the general case (point-slope)?

Even if you are given the slope and y-intercept, you can write y=b+m\left( x-0 \right).

If for some reason you need the equation in slope-intercept form, you can always “simplify” the point-slope form.

But don’t you need slope-intercept to graph? No, you don’t. Given the point-slope form you can easily identify a point on the line,\left( {{x}_{0}},{{y}_{0}} \right), start there and use the slope to move to another point. That is the same thing you do using the slope-intercept form except you don’t have to keep reminding your kids that the y-intercept, b, is really the point (0, b) and that’s where you start. Then there is the little problem of what do you do if zero is not in the domain of your problem.

Help me. Please talk to your colleagues who teach pre-algebra, Algebra 1, Geometry, Algebra 2 and pre-calculus. Help them get the kids off on the right foot.

Whenever I mention this to AP Calculus teachers they all agree with me. Whenever you grade the AP Calculus exams you see kids starting with y = mx + b and making algebra mistakes finding b.

Inequalities

Posted on by
1

This is an “extra” post on a technique that students are using a lot right now in graphing functions and working on optimization problems.

In analyzing a derivative to find critical points and then the intervals where the function increases and decreases you need to solve these inequalities. I’ve observed many students solving inequalities the hard way.

By that I mean they will pick a number in each interval between the critical points and then substitute it into the derivative and do a lot of arithmetic to determine whether the derivative is positive or negative. Arithmetic is not necessary, when all you really need is the sign of the derivative. The method I suggest is easier and involves no arithmetic and therefore precludes any arithmetic mistakes

A complete discussion of this idea with examples click here or look on my Resources page.

The Range of the Inverse

Posted on by
Reply

The last two post discussed inverse functions and some concerns about them. We continue that today be considering that fact that sometimes the inverse of a function is not a function, and what can be done in that case.

Since the square of both 3 and –3 is 9. Which number should you get when you unsquare 9? Is the result, 3 or –3?

Mathematicians want, for practical reasons, inverses to be functions. If the original function is not strictly monotonic then the inverse will not be a function. That is, if there are places on the original function that have the same y-values then the inverse (set of ordered pairs found by reversing the function’s ordered pairs) will not be a function. If some horizontal line intersects the graph of the function more than once, the inverse will not be a function.

While it may seem a bit too convenient, what is done is that the range of the inverse is restricted so that the inverse is a function. So for f (x) = x2 the range of the inverse is restricted to non-negative values. So f -1(9) = 3 and f -1(10) = \sqrt{10}  where it is understood that this represents a non-negative number. This is why {{f}^{-1}}\left( {{a}^{2}} \right)=\sqrt{{{a}^{2}}}=\left| a \right|. So that if a = –4, \sqrt{{{a}^{2}}}=\left| -4 \right|=4.

The restriction is arbitrary. It would be just as possible to make the range all non-positive numbers. While arbitrary, the restriction is not unreasonable. After all, once we understand this, we can easily find the other value if we need it. This is also necessary for calculators to work; the process they use to compute the value can only return one value. The (restricted) ranges of the common functions are what mathematicians feel are the most useful.

None of the trigonometric functions pass the horizontal line test; none of their inverses are functions until the ranges have been restricted. These restrictions are in the textbooks. For example: The domain of sin-1(x) is -1\le x\le 1, these are the output values of the sin(x); the range is restricted to \displaystyle -\tfrac{\pi }{2}\le {{\sin }^{-1}}\left( x \right)\le \tfrac{\pi }{2}. Because the signs of the trig functions are different outside of the first quadrant and in order to make as many of the inverses as possible continuous, each inverse trig function has a different range. You will find these in your textbook. They are built into calculators and computers. This can be a little confusing for students, but there is not much that can be done about that.

This is the third of 5 posts on inverses. The next post: The Calculus of Inverses.

Writing Inverses

Posted on by
Reply

In my last post I identified two “problems” related to inverses. The first of these is that there may be no string of operations, no algebra or arithmetic, which tells us how to evaluate the inverse function.

For simple functions you can find the inverse function by switching the x and the y and then solving for y. If you can do that, this produces a nice expression for the inverse. Alas usually you cannot do that.

What to do?

What you can do is invent a name and/or a symbol for the new function. So if f(x) = x2, we write f -1(x) = \sqrt{x} and we think we have solved the problem. We have not. While I can write \sqrt{x}, what arithmetic can I do to express this number as a decimal? There is an algorithm for this; (you can find it on the internet by searching for “square root algorithm”). You can use a calculator or look in a table as we did back in the “old days.” But that is not the same as performing a series of arithmetic or algebraic operations.

And if \sqrt{10} does not slow you down, how about sin-1(0.12345)? The only hope in some cases is to try to solve something like x2 = 10 or sin(y) = 0.12345, not much hope there. We are left with using technology of some sort if we need a number (decimal); calculators have buttons for square roots and inverse sines. But sometimes writing \sqrt{10} or  sin-1(0.12345) is good enough.

Making up a new function or symbol to “solve” a problem, even if that function cannot be written as a string of operations is actually fairly common. The sin(x) is defined as the y-coordinate of a point on the unit circle. Except for some special numbers you cannot find y-coordinates that easily. You have seen others already. All the trigonometric functions and their inverses as well as logarithmic functions are of this sort. Mathematics is full of them.

The next post will discuss the other problem: the inverse of a function may not be a function. Since there are two numbers whose square is 9, what is the “unsquare” of 9; is it 3 or –3?

This is the second of 5 posts on inverses.

Inverses

Posted on by
Reply

The next few posts will concern functions and their inverses. Today we will just get into the basics which, hopefully, students know from their work prior to calculus. Of course, they will have forgotten some of this and claim they never learned it. (Which may be correct, but one hopes they were taught it.) This is one of the places where a brief review just before teaching the calculus of inverses might be useful.

When starting out with functions we are given a value of the input or independent variable, x, and are asked to compute the output value or the dependent variable, y. Then, to mix things up, you may be given an output value and asked to find the input value that produces it. With the beginning functions this is not too difficult; that is, there are algebraic techniques that can be used. If you have to do a number of these, you can easily write an expression solved for x that you can use to find the y’s.

To streamline all this mathematicians use the concept of the inverse of a function. If a function is a set of ordered pairs (a, b) or (x, f (x)) then the inverse is defined as the set with these ordered pairs with the coordinates reversed; (b, a) or (f (x), x). Since this last looks a bit strange we define a new notation f -1(x) to denote the inverse of f(x). That is f -1(x) is the inverse function of the original function f(x). The ordered pairs are now (x, f -1(x)).

For very simple functions the inverse can be found by switching the x and y in the original and the solving for y. So if f (x) = 2x + 3 we write x = 2y + 3 and solve to get y = ½(x – 3). So f -1(x) = (½)(x– 3).

Notice that f (f -1(x)) = 2(½(x – 3))+3 = x.

Several things to note at this point:

  • Inverses occur in pairs. The inverse of the inverse is the original function.
  • The inverse undoes whatever the function did and returns the original input value. In symbols this is  f -1(f (x)) = f (f -1(x))=x.
  • The points (a, b) and (b, a) are symmetric to the line y = x and therefore the inverse of a function has a graph that is the reflection of the function’s graph across the line y = x. The function and its inverse are symmetric to this line.
  • The domain and range switch places: the domain of the inverse is the range of the function, and the range of the inverse is the domain of the function.

There are also several problems that need to be addressed.

  • There may be no string of operations, no “algebra”, which will produce the output for the inverse function. We cannot write an algebraic expression to find the number whose seventh power is 10. What do we do in this case?
  • The inverse of a function may not be a function. Since there are two numbers whose square is 9, what is the “unsquare” of 9; is it 3 or –3? When does this happen? Since it is really useful for the inverse to be a function, what can be done about this?

These two “problems” will be the subjects of my next two post.

(This started out as one post and has grown to a series 5.)

Show me the Math!

Posted on by
Reply

Is God a Mathematician? by Mario Livio begins

When you work in cosmology … one of the facts of life becomes the weekly letter, e-mail, or fax from someone who wants to describe to you his own theory of the universe (yes, they are invariably men). The biggest mistake you can make is to politely answer that you would like to learn more. This immediately results in an endless barrage of messages. So how can you prevent the assault? The particular tactic I found to be quite useful (short of the impolite act of not answering at all) is to point out the true fact that as long as his theory is not precisely formulated in the language of mathematics, it is impossible to assess its relevance. This response stops most amateur cosmologists in their tracks. … Mathematics is the solid scaffolding that holds together any theory of the universe.

Is God a Mathematician? discusses the question of whether mathematics was invented or discovered. Dr. Livio’s other popular books include The Accelerating Universe (cosmology), The Golden Ratio: The Story of Phi, the World’s most Astounding Number, and The Equation that Couldn’t be Solved: How Mathematical Genius Discovered the Language of Symmetry. All are excellent reads for teachers and students. 

Deltas and Epsilons

Posted on by
Reply
The Formal Definition of Limit

Teachers are often concerned that the Advanced Placement Calculus tests do not test the formal definition of limit and the delta-epsilon idea. I think there are two reasons for this.

  1. For linear functions the relationship is always \delta =\frac{\varepsilon }{\left| m \right|} where m is the slope of the line. Anyone can memorize that, so testing it does not provide any evidence that the student knows anything. For any other function (polynomials of higher degree, trigonometric functions, etc.) some special one-time “trick” is required, often different for each type of function. Thus, the question becomes unreasonably difficult even for one who understands the concept.
  2. As a multiple choice question, since “none of these” is never a choice on AP tests, the smallest answer must be correct. If \delta =\tfrac{1}{2}\varepsilon  is correct, then so is \delta =\tfrac{1}{3}\varepsilon ,\ \delta =\tfrac{1}{10}\varepsilon  etc. Again no real knowledge of the definition is required – just choose the smallest delta.

Of course, the definition of limit is important. You may teach it in your class. It just will not appear on the AP Calculus exams.

Here are some notes The Definition of Limit contributed by Paul A . Foerster of San Antonio, Texas, that will help your students understand the concept.