Author Archives: Lin McMullin

Rolle’s Theorem

Posted on by
Reply

Rolle’s theorem says that if a function is continuous on a closed interval [a, b], differentiable on the open interval (a, b) and if f (a) = f (b), then there exists a number c in the open interval (a, b) such that {f}'\left( c \right)=0.  (“There exists a number” means that there is at least one such number; there may be more than one.)

The proof has two cases:

Case I: The function is constant (all of the values of the function are the same as f (a) and f (b)). The derivative of a constant is zero so any (every, all) value(s) in the open interval qualifies as c.

Case II: If the function is not constant then it must have a maximum or minimum in the open interval (a, b) by the Extreme Value Theorem. So, by Fermat’s theorem (see this post) the derivative at that point must be zero.

So, Fermat’s theorem makes Rolle’s theorem a piece of cake.

A lemma is a theorem whose result is used in the next theorem and makes it easier to prove. So Fermat’s theorem is a lemma for Rolle’s theorem.

On the other hand, a corollary is a theorem is a result (theorem) that follows easily from the previous theorem. So, Rolle’s theorem could also be called a corollary of Fremat’s theorem.

Rolle’s theorem makes a major appearance in the MVT and then more or less disappears from the stage. When you find critical number or critical points you are using Fermat’s theorem.

I like this proof because it’s so simple. It really just comes immediately from Fermat’s theorem.

The next post: The Mean Value Theorem.

Fermat’s Penultimate Theorem

Posted on by
Reply

I have mixed feelings about proof in high school math and high school calculus. I am not one for proving everything. For one thing, it cannot be done and, if it could be done, proof would become the whole focus of high school math. Proofs are not the focus of first-year calculus or AP calculus. The place for proving “everything” is a real analysis course in college.

However, students should know about proof and there are places where you can demonstrate some of the power of proof and show how proof works in calculus.
It is important, I think, that students know why a theorem is true; this helps in understanding what the theorem means. Some, but by no means all, proofs can show the student why the theorem is true. With other theorems there may be easier ways than a proof to convince someone of its truth.

In this and the next three posts, I propose to look at three theorems, the definitions used in them, and the ideas in their proofs. These are the theorems that lead up to the Mean Value Theorem (MVT). The MVT is a major result in calculus has many uses. Here goes:

Fermat’s theorem (not his famous “last” theorem, but an earlier one) says, that if a function is continuous on a closed interval and has a maximum (or minimum) value on that interval at x = c, then the derivative at x = c is either zero or does not exist.

The proof goes like this:
There are two cases. In each case we will look at the limit of the difference quotient that defines the derivative at x = c, namely, \frac{f\left( c+h \right)-f\left( c \right)}{h} and look at what happens as h approaches 0 from the left and from the right. These two limits are the same and equal to the derivative if, and only if, the derivative at c exists.

Also note that since we are assuming f(c) is a maximum, f (c) ≥ f (c + h) regardless of whether h is positive or negative. The numerator of the difference quotient is always zero or negative. Then if in the denominator h < 0, the quotient is non-positive; likewise, if h > 0, the quotient is non-negative.

Case I: The two limits are not equal. In this case the derivative does not exist. This could occur with a piecewise function, where two pieces with different derivatives meet at x = c.

Case II: The limits are equal. In this case the limit from the left (h < 0) must be greater than or equal to zero (since the function is increasing there) and the limit from the right (h > 0) must be less than or equal to zero. Then, the only way the limits can be equal is if both limits are zero; therefore the derivative is zero.

Any place where the derivative of a continuous function is zero or undefined is called a critical point and the number c is called a critical number (new definitions).

I think this proof is interesting because while there are lots of symbols flying around the key is interpreting what kind of number (positive, zero or negative) the symbols represent. Another thing I like is having to “read” the symbols and see that 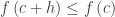f\left( c+h \right)\le f\left( c \right) and therefore f\left( c+h \right)-f\left( c \right)\le 0

The next post will discuss Rolle’s theorem.

The Chain Rule

Posted on by
Reply

Except for the simplest functions, a procedure known as the Chain Rule is very helpful and often necessary to find derivatives. You can start with an example such as finding the derivative of  {{\left( 2x+7 \right)}^{2}}.  Most students will expand the binomial to get 4{{x}^{2}}+28x+49 and differentiate the result to get 8x+28. They will try the same approach with {{\left( 2x+7 \right)}^{3}} and then you can hit them with {{\left( 2x+7 \right)}^{53}}.  They will see the need for a short cut at once. What to do?

The explanation runs like this. Let u\left( x \right)={{x}^{53}} and let v\left( x \right)=2x+7. Then our original expression becomes {{\left( 2x+7 \right)}^{53}}=u\left( v\left( x \right) \right) a composition of functions. The Chain Rule is used for differentiating compositions. Students must get good at recognizing compositions. The differentiation is done from the outside, working inward.  It is done in the exact opposite order than the procedure for evaluating expression. To evaluate the expression above you (1) evaluate the expression inside the parentheses and the (2) raise that result to the 53 power. To differentiate you (1) use the power rule to differentiate the 53 power of whatever is inside, this gives 53{{\left( 2x+7 \right)}^{52}}, the (2) differentiate the \left( 2x+7 \right) which give 2 and multiply the results: 53{{\left( 2x+{{7}^{52}} \right)}^{52}}(2)=106{{\left( 2x+7 \right)}^{52}}. Symbolically, this looks like {u}'\left( v\left( x \right) \right){v}'\left( x \right) or {f}'\left( g\left( x \right) \right){g}'\left( x \right). This can be extended to compositions of more than two functions:

\displaystyle \frac{d}{dx}f\left( g\left( h\left( x \right) \right) \right)={f}'\left( g\left( h\left( x \right) \right) \right){g}'\left( h\left( x \right) \right){h}'\left( x \right)

The cartoon below is from Courtney Gibbons’ great collection of math cartoons (http://brownsharpie.courtneygibbons.org/) may help you kids remember this:


I have been looking for a way to illustrate the Chain Rule graphically, but to no avail. The closest I could come up with is this: Consider f\left( x \right)=\sin \left( 3x \right). This function takes on all the values of y=\sin \left( x \right) in order in one-third the time. (That is its period is one-third of the period of y=\sin \left( x \right). Since this is true, it must go through the values three times as fast; thus, its derivative (it’s rate of change) must be three times the derivative of the sine: {f}'\left( x \right)=3\cos \left( 3x \right).

The students will need some practice on using the Chain Rule. I suggest a number of simple (single compositions) first and then a few longer ones and maybe one or two “monsters” just for fun once they get the idea.

The Chain Rule doesn’t end with just being able to differentiate complicated expressions; it will also form the basis for implicit differentiation, finding the derivative of a function’s inverse and Related Rate problems among others things.

Finally, here is a way to develop the Chain Rule which is probably different and a little more intuitive from what you will find in your textbook. (After a suggestion by Paul Zorn on the AP Calculus EDG October 14, 2002)

Let f be a function differentiable at x=a, and let g be a function that is differentiable at x=b and such that g\left( b \right)=a. Then, near x=a we can use the local linear approximation of f and g to find  \frac{d}{dx}f\left( g\left( b \right) \right):

f\left( x \right)\approx f\left( a \right)+{f}'\left( a \right)\left( x-a \right)

f\left( g\left( x \right) \right)\approx f\left( a \right)+{f}'\left( a \right)\left( g\left( x \right)-a \right)=f\left( a \right)+{f}'\left( a \right)g\left( x \right)-a {f}'\left( a \right)

\displaystyle \frac{d}{dx}f\left( g\left( x \right) \right)=0+{f}'\left( a \right){g}'\left( x \right)-0

\displaystyle\frac{d}{dx}f\left( g\left( b \right) \right)={f}'\left( g\left( b \right) \right){g}'\left( b \right)

Derivative Rules III

Posted on by
1

The Quotient Rule

This approach to the quotient rule is credited to Maria Gaetana Agnesi (1718 – 1799) who wrote the first known mathematics textbook Analytical Institutions (1748) to help her brothers learn algebra.

The quotient rule can also be proven from the definition of derivative. But here is a simpler approach – as a corollary of the product rule.

Begin by letting \displaystyle h\left( x \right)=\frac{f\left( x \right)}{g\left( x \right)}.

Then

f\left( x \right)=h\left( x \right)g\left( x \right) and {f}'\left( x \right)=g\left( x \right){h}'\left( x \right)+h\left( x \right){g}'\left( x \right).

Then solving for {h}'\left( x \right):

\displaystyle {h}'\left( x \right)=\frac{{f}'\left( x \right)-h\left( x \right){g}'\left( x \right)}{g\left( x \right)}

\displaystyle =\frac{{f}'\left( x \right)-\frac{f\left( x \right)}{g\left( x \right)}{g}'\left( x \right)}{g\left( x \right)}

\displaystyle =\frac{g\left( x \right){f}'\left( x \right)-f\left( x \right){g}'\left( x \right)}{{{\left( g\left( x \right) \right)}^{2}}}

Mnemonics

I’m not really one for mnemonics. I cannot spell SOHCOHTOA without saying to myself, “sine, opposite over hypotenuse; cosine, adjacent …” It seems better to me anyway to have student just memorize the formulas in words using the correct terms:

The derivative of a product is the first factor times the derivative of the second plus the second factor times the derivative of the first.

The derivative of a quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator all divided by the square of the denominator.

But whatever works for you. Lo Di Hi

The Derivative Rules II

Posted on by
Reply

The Product Rule

Students naturally figure that the derivative of the product of two functions is the product of their derivatives. So first you must disabuse them of this idea. That is easy enough to do.

Consider two functions and their derivatives  f\left( x \right)={{x}^{7}}\text{ with }{f}'\left( x \right)=7{{x}^{6}} and g\left( x \right)={{x}^{5}}\text{ with }{g}'\left( x \right)=5{{x}^{4}}. So now f\left( x \right)g\left( x \right)={{x}^{12}} and \frac{d}{dx}\left( f\left( x \right)g\left( x \right) \right)=12{{x}^{11}}. Is this {f}'\left( x \right){g}'\left( x \right)=35{{x}^{10}}? No it is not!

But all is not lost. How can we get the correct answer from the original functions and their derivatives? Start with the 12; this comes from adding the 7 and 5 so the correct answer must be something along the lines of
12{{x}^{11}}=7{{x}^{6}}\_\_\_\_\_+5{{x}^{4}}\_\_\_\_\_

From the expression we already have what can we put in the blank spaces to get the similar terms with {{x}^{11}}? How about the original functions?
12{{x}^{11}}=7{{x}^{6}}\underline{{{x}^{5}}}+5{{x}^{4}}\underline{{{x}^{7}}}

And there is the product rule right there

You can use this same idea with other products.

You may also use the definition of derivative which you can find in most books, but bringing in zero in the form of -f\left( x+h)g\left( x \right) \right)+f\left( x+h)g\left( x \right) \right) is hardly something you would expect anyone to figure out by themselves. As I mentioned, I’m more into explaining than proving.

(This example is one of many I learned from Paul Foerster. Thanks again, Paul)

Here is another approach suggested by Dick Sisley. Thank you, Dick.

If students already know the Chain Rule:

Then–let h(x)= f(x)* f(x) = (f(x))^2 (this is a key equivalence.)

Next use the Chain Rule to get h'(x)= 2*f(x)*f ‘(x)= 2*(f ‘(x)*f(x)).

Now note that 2*(f ‘(x)*f(x))= f ‘(x)* f(x) + f ‘(x)* f(x)

The key step is then to let h(x) = f(x)*g(x) and ask students to use the result for f ‘(x)*f(x) to conjecture the result for f(x)*g(x).  There have always been some who come up with f ‘(x)*g(x) + f(x)*g'(x).  Others come up with other, non-equivalent conjectures.  But there is a way to evaluate the likelihood of every conjecture.

Use h(x)= f(x)*f(x)= x * x. We know the result should be 2*x.

Use h(x)= f(x)*f(x) = x^2 * x. We know the result should be 3*x^2.

etc.

We can experiment with products such as sin(x)*x^2.  If we use the correct conjecture pattern, we can test the reasonableness of the result using the numerical derivative feature of a graphing calculator on values the students select.

Updated 11-6-2013

Next The Quotient Rule.

The Derivative Rules I

Posted on by
2

The time is approaching when you will want and need to find derivatives quickly. I am afraid that, with the exception of the product rule, I have no particularly clever ideas of how to how to teach this.

I am inclined to offer some explanation, short of a lot of proofs, to students as to why the rules and procedure are what they are. To that end I would start with some simple formulas using the (limit) definition of derivative.

  • The derivative of constant times a function is the constant times the derivative of the function. This is easy enough to show from the definition since constants may be factors out of limits
  • Likewise, the derivative of a sum or difference of functions is the sum of difference of the derivatives of the functions. This too follows easily from the properties of limits.
  • For powers, keeping in mind the guesses from mention previously in the previous two posts “The Derivative I and II”, I suggest the method that all the books show. For example to find the derivative of x3 write

\displaystyle \underset{h\to 0}{\mathop{\lim }}\,\frac{{{\left( x+h \right)}^{3}}-{{x}^{3}}}{h}=\underset{h\to 0}{\mathop{\lim }}\,\frac{{{x}^{3}}+3{{x}^{2}}h+3x{{h}^{2}}+{{h}^{3}}-{{x}^{3}}}{h}

\displaystyle =\underset{h\to 0}{\mathop{\lim }}\,\left( 3{{x}^{2}}h+3x{{h}^{2}} \right)=3{{x}^{2}}

And perhaps a one or two more until the students are convinced of the pattern.

  • For trigonometric functions follow your textbook: use the definition and the formula for the sine of the sum of two numbers along with the two special limits.

The next post will concern the product and quotient rules.

 

 

 

 

 

 

Difference Quotients II

Posted on by
1
The Symmetric Difference Quotient

In the last post we defined the Forward Difference Quotient (FDQ) and the Backward Difference Quotient (BDQ). The average of the FDQ and the BDQ is called the Symmetric Difference Quotient (SDQ):

\displaystyle \frac{f\left( x+h \right)-f\left( x-h \right)}{2h}

You may be forgiven if you think this might be a better expression to use to find the derivative. It has its advantages. In fact, this is the expression used in many calculators to compute the numerical value of the derivative at a point; in calculators it is called nDeriv. Usually, it works pretty well. But if you try to find the derivative of the absolute value of x at x = 0 it will tell you the derivative is 0, which is wrong. The absolute value function is not locally linear at the origin and has no derivative there.

What went wrong?  Read the expression above. The numerator is the difference of the function values at the same distance, h, on both sides of x. Since, for the absolute value function with x = 0, these values are the same, their difference is 0. The SDQ never looks at x = 0 and doesn’t realize there is no derivative there. Thus, the limit of the SDQ is not the derivative.

This problem does not occur with the definition of derivative, since for that limit to exist the limits as h approaches zero from both sides must be equal. For the absolute value function the limit from the left is –1 and the limit from the right is +1 and therefore there is no limit and no derivative there.

Since most functions we will consider are differentiable, most of the time the SDQ and nDeriv are okay to use.

Seeing Difference Quotients Converge

This is an activity to see difference quotients graphically. Use a graphing calculator or a graphing program on a computer. One with a slider feature is better although I’ll also tell you how to use a calculator without this feature.

  1. Enter the function you want to consider as Y1 in your calculator or give it a name if you are using a computer. This is so later you can change the function without having to re-enter the next three equations.
  2. Enter the FDQ as Y2 using Y1 as the function. See Figure 1 below.
  3. Enter the BDQ as Y3 again using Y1 as the function.
  4. Enter the SDQ as Y3 again using Y1 as the function.
  5. Either set up a slider for h or go to the home screen and store a value for h. In the latter case you will have to return to the home screen and change the values.

Now graph all four functions. As you change the values of h with the slider or from the home screen, you should see three similar graphs (the difference quotients) along with the first function you entered. As h approaches zero, the three similar graphs should come together (converge) on the graph of the derivative. See Figures 2 and 3 below.

Change the first function. Some good functions to try are y = x3 – 4x, y = x3/3, y = sin(x) and don’t forget y = |x|. Try guessing the equation of the derivative.

Figure 2 Shows y = x3/3 in Black with the three difference quotients, h is about 2.

Figure 3 shows the same graph with h almost 0; the three difference quotients, now almost on top of each other, are closing in on the derivative.

Here is a link to a Desmos demonstration of the three difference quotients