Monthly Archives: May 2013

Locally Linear L’Hôpital

Posted on by
Reply

I’ll begin with a lemma. (I like to do a lemma now and then if for no other reason than having an excuse to explain what a lemma is – a simple theorem that is used in proving the main theorem.)

Lemma: If two lines intersect on the x-axis, then for any x the ratio of their y-coordinates is equal to the ratio of their slopes.

Proof: Two lines with slopes of m1 and m2 that intersect at (a, 0) on the x-axis have equations y1 = m1(x – a) and y2 = m2(x – a). Then

\displaystyle \frac{{{y}_{1}}}{{{y}_{2}}}=\frac{{{m}_{1}}\left( x-a \right)}{{{m}_{2}}\left( x-a \right)}=\frac{{{m}_{1}}}{{{m}_{2}}}

L’Hôpital’s Rule (Theorem): If f and g are differentiable near x = a and f(a) = g(a) = 0, then

\displaystyle \underset{x\to a}{\mathop{\lim }}\,\frac{f\left( x \right)}{g\left( x \right)}=\underset{x\to a}{\mathop{\lim }}\,\frac{{f}'\left( x \right)}{{g}'\left( x \right)}

if the limit exists.

The fact that f(a) = g(a) = 0 means that the two functions intersect on the x-axis at (a, 0). For example, the functions f(x) = tan(x) and g(x) = sin(x) have this property at \left( \pi ,0 \right).

Figure 1. y = tan(x) in red and y = sin(x) in blue

Figure 1. y = tan(x) in red and y = sin(x) in blue

Now zoom-in several times centered at \left( \pi ,0 \right).

Figure 2. The previous graph zoomed in.

Figure 2. The previous graph zoomed in.

Whoa!

That looks like lines!!

It’s the local linearity property of differentiable functions – if you zoom-in enough any differentiable function eventually looks linear. So maybe near \left( \pi ,0 \right) the lemma applies. The only difference is that the slopes of the “lines” are the derivatives so

\displaystyle \underset{x\to a}{\mathop{\lim }}\,\frac{f\left( x \right)}{g\left( x \right)}=\underset{x\to a}{\mathop{\lim }}\,\frac{{f}'\left( x \right)}{{g}'\left( x \right)}

 Now that does not quite prove L’Hôpital’s Rule, but it should give you and your students a good idea of why L’Hôpital’s Rule is true.

Then in our example:

\displaystyle \underset{x\to \pi }{\mathop{\lim }}\,\frac{\tan \left( x \right)}{\sin \left( x \right)}=\underset{x\to \pi }{\mathop{\lim }}\,\frac{\frac{1}{{{\left( \cos \left( x \right) \right)}^{2}}}}{\cos \left( x \right)}=\underset{x\to \pi }{\mathop{\lim }}\,\frac{1}{{{\left( \cos \left( x \right) \right)}^{3}}}=\frac{1}{{{\left( \cos \left( \pi \right) \right)}^{3}}}=-1

But isn’t that obvious from Figure 2?

Think about it.

More on this next time.

 

 

 

 

 

Summer Reading

Posted on by
Reply

I like to read and I read a lot. I often have a novel going. Lately since I’ve been writing this Blog, I’ve been reading other blogs. I’ve listed a few in the right-side column but here are two that might interest you. (Since deleted)

Wired Magazine

Wired magazine  has a lot of interesting articles on science and technology. They also publish a collection of Science Blogs. If you are interested in what’s going on in science this may be the place to start. Samuel Arbesman writes the math blog entitled Social Dimensions that is more focused on things mathematical. Wired also has the latest in math news like their piece on the “Unknown Mathematician Proves Elusive Property of Prime Numbers”

 dy/dan

Another of my favorites is a blog called dy/dan  by Dan Meyer who always has interesting ideas and interesting problems to discuss from all levels of teaching mathematics. The blog has lessons on lots of topics.

Dan recently posted the video below. It is a talk by Uri Theisman entitled “Keeping Our Eyes on the Prize” concerning equity, race and the opportunity to learn. Dr. Theisman is from the Charles A. Dana Center at the University of Texas at Austin. He is a recognized authority on education. The talk was given at the NCTM meeting April 19, 2103. It runs about 50 minutes and is certainly worth the time. Anyone interested in equity and the opportunity to learn will find this interesting.  Here is Dr. Theisman’s own summary:

There are two factors that shape inequality in this country and educational achievement inequality. The big one is poverty. But a really big one is an opportunity to learn. As citizens, we need to work on poverty and income inequality or our democracy is threatened. As mathematics educators … we need to work on opportunity to learn. It cannot be that the accident of where a child lives or the particulars of their birth determine their mathematics education.

Uri Treisman’s “Keeping Our Eyes on the Prize” – NCTM 2013 from Dan Meyer on Vimeo.

Is God a Mathematician?

Finally, if you are looking for an actual book to read, I recommend again Is God a Mathematician? by Mario Livio. I written about this book before here.

Absolute Value

Posted on by
Reply

The answers to the True-False quiz at the end of the last post are all false. This brings us to absolute value, another topic I want to concentrate on for my upcoming Algebra 1 class. Absolute value becomes a concern in calculus too which I will discuss as the last example below.

There a several “definitions” of absolute value that I’ve seen over the years which I mostly do not like

  • The number without a sign – awful: all numbers except zero have a sign
  • The distance from zero on the number line – true, but not too useful especially with variables
  • The larger of a number and its opposite – true, but not to useful with variables

So I propose to give them an algorithm: If the number is positive, then the absolute value is the same number; if the number is negative, then its absolute value is its opposite. Of course, this is really the definition.

So I’ll soon express this in symbols

\left| a \right|=\left\{ \begin{matrix} a & \text{if }a\ge 0 \\ -a & \text{if }a<0 \\ \end{matrix} \right.

Now interestingly this is probably the first piecewise defined function an Algebra 1 student may see, or at least the first one that’s not artificial.  So this is a good place to start talking about piecewise defined function and the importance of talking about the domain. And of course, we’ll have to take a look at the graph.

Sometimes we will have to start solving equations and inequalities with absolute values. So here is the next thing I understand but do not like and will try to avoid. Solve the equation: \left| x \right|=3 , Answer including work: x=\pm 3. But I think a longer way around is also better:

If x<0 then \left| x \right|=-x=3 so x=-3 or if x>0, then \left| x \right|=x=3 Solution: x=3 or x=-3.

Longer? Sure. I hope that by making the students write that a few times that when they get to solving  \left| x \right|>3 that it will be natural to say

If  x<0 then \left| x \right|=-x>3  so x<-3 or if x>0, then \left| x \right|=x>3 Solution:  x<-3 or x>3

The last case may take a little more discussion. Solve \left| x \right|<3. Starting the same way

If x<0 then \left| x \right|=-x<3 so x>-3 which really means -3<x<0

if x>0, then \left| x \right|=x<3 which really means 0\le x<3 . Then the union of these two sets looks like an intersection. The solution is -3<x<3

Quite often the equation and the two types of inequalities are treated as separate problems: with = you go with \pm  on the other side, with > you have a union pointing away from the origin and with < you have somehow an intersection.  Who needs to remember all that when this idea works all the time?

Example:  Solve \left| 4x-10 \right|<8

If 4x-10<0, then x<\tfrac{5}{2} and \left| 4x-10 \right|=-\left( 4x-10 \right)=-4x+10<8, so -4x<-2 and x>\tfrac{1}{2} or more precisely  \tfrac{1}{2} If latex 4x-10\ge 0$, then x\ge \tfrac{5}{2}  and \left| 4x-10 \right|=4x-10<8, so 4x<18 and x<\tfrac{9}{2} or more precisely \tfrac{5}{2}<x<\tfrac{9}{2}. The union again becomes an intersection and the answer is \tfrac{1}{2}<x<\tfrac{9}{2}

Finally an example from calculus. On the 2008 AB exam, question 5 asked student to find the particular solution of a differential equation with the initial condition f\left( 2 \right)=0. After separating the variables, integrating, including the “+C” and substituting the initial condition students arrived at this equation which they now need to solve for y:

 \displaystyle \left| y-1 \right|={{e}^{\tfrac{1}{2}-\tfrac{1}{x}}}

How can you lose the absolute value sign? Simple, near the initial condition where y = 0,  \left( y-1 \right)<0 so replace \left| y-1 \right| with -\left( y-1 \right) and then go ahead and solve for y

 \displaystyle -\left( y-1 \right)={{e}^{\tfrac{1}{2}-\tfrac{1}{x}}}

\displaystyle y=1-{{e}^{\tfrac{1}{2}-\tfrac{1}{x}}}

I don’t think I’ll try this one in Algebra 1, but maybe it will come in handy when they get to calculus.

The Opposite of Negative

Posted on by
5

Next year, for the first time in 15 years, I am going to be teaching high school full-time. While I have enjoyed writing and working primarily with teachers for the last 15 years, I’m looking forward to “going back to the classroom” as they say. It looks like I’ll be teaching BC calculus and Algebra 1 – two of my favorite classes. I’m very positive about that.

With that in mind I have been thinking of some of the things I want to be sure I get right in the Algebra 1 classes to get the kids off to a good start. So a few of my blogs in the coming year may be on Algebra 1 topics with the view of having students do things right from the start and not having to relearn things when they get to calculus.

So here is the first thing I want to be sure to work on: the m-dash also known as the minus sign.

According to Wikipedia:

The minus sign (−) has three main uses in mathematics:

  1. The subtraction operator: A binary operator to indicate the operation of subtraction, as in 5 − 3 = 2. Subtraction is the inverse of addition.
  2. Directly in front of a number and when it is not a subtraction operator it means a negative number. For instance −5 is negative 5.
  3. A unary operator that acts as an instruction to replace the operand by its opposite. For example, if x is 3, then −x is −3, but if x is −3, then −x is 3. Similarly, −(−2) is equal to 2.

Using the same symbol understandably can confuse beginning math students. I am not going to invent new symbols so I will just have to be careful with what I say and let the kids say. And I have to say it right , if I expect them to.

When used between two numbers or two expressions with variables the symbol means subtraction. That’s pretty easy to spot and understand in context.  But when used alone in front of something the minus sign means different things.

The m-dash may always be read “opposite.” So “–a” is read “the opposite of a” and not “negative a.”  Likewise, –5 is read “the opposite of five.”

There is only one instance where the m-dash may be read “negative.” When it is used in front of a number it indicates a negative number so      “–5” is also correctly read “negative five.” This is the only time the m-dash should be read “negative.”  Things like “–a” should always be read “the opposite of a” and never read “negative a.”

There was a time when the folks who write math books tried to make the distinction by using a slightly raised dash to indicate negative number so negative 3 was written  “–3.” This has carried over into calculators where the key marked “(–)” is used for “negative” and “opposite.” and is printed on the screen as a shorter and slightly raised dash. The subtraction key is only used for subtraction.

Oh, if it were only that simple. What do you do with –(–5)? Not really a problem the “opposite of the opposite of 5” and the “opposite of negative 5” are both 5.

I’ll know I’ve succeeded when everyone can get 100% on this little True-False quiz:

  1. The opposite of a number is a negative.
  2. –x < 0
  3. x > 0
  4. | x | = x
  5. |– x |= x

Answers are in my next post.

Revised 10-27-2018

A Standard Problem?

Posted on by
Reply

Sometimes even the simplest problems can lead to interesting places. I got interested in this ordinary textbook problem a few months ago while observing an AB calculus class. Here is how my thinking went written as a series of exercises:

Original exercise: Find the point(s) on the parabola y = x2 that are closest to the point (0, 2).

The solution is straightforward:

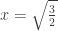Let z(x) be the distance from (0, 2) to the point (x, x2). Then \displaystyle z\left( x \right)=\sqrt{{{\left( x-0 \right)}^{2}}+{{\left( {{x}^{2}}-2 \right)}^{2}}}and setting the derivative equal to zero, we find the critical points at x = 0 a local maximum and x=-\sqrt{\tfrac{3}{2}} and x=\sqrt{\tfrac{3}{2}} both absolute minimums located symmetrically to the y-axis.

The students had some trouble understanding what was going on. I suggested they consider a point moving along the parabola starting high on the left side. As the point comes down the graph its distance from \left( 0,2 \right) gets shorter until it reaches some minimum length somewhere. Then the distance gets longer again until – where? Obviously, at the origin. Then symmetry takes over and the distance decreases again until it reaches a second minimum directly across the y-axis from the first point, after which it increases forever.

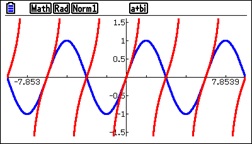
Exercise 1: Sketch the graph of the distance function, z(x), on top of the graph of the parabola. Give the exact coordinates of the maximum point without doing any computations. Discuss the y-coordinates of the minimum points.

It then occurred to me that there is nothing sacred about (0, 2). We could use any point on the y-axis, . Or could we? I pictured a circle centered at the point (0, a) on the y-axis tangent to the parabola (i.e. tangent to the tangent line of the parabola). The radius of such a circle is the minimum distance for that y-axis center point.

Exercise 2: If the point is below the origin then obviously the minimum distance is the distance directly up to the origin. There are places above the x-axis where the origin is the closest point. For what values of a is the origin the closest point? Use the circle mentioned above to explain how this is possible.

The distance graph that we drew above has a W shape similar to the shape of some 4th degree polynomials (note: z(x) is not a 4th degree polynomial, it is not even a polynomial). So next I drew the graph of z’(x), the first derivative of z; this graph is similar to a cubic polynomial (again it is not a polynomial)

Exercise 3: Without actually computing the derivative’s equation, sketch the graph of the derivative with the graph of the parabola and the distance function’s graph. Be sure the critical points are where they should be.

Exercise 4: Use a graphing program or a graphing calculator do draw the parabola, z(x) and z’(x) and use it to check your sketches.

Project: Using a suitable program (Winplot, Geogebra, etc.) set up an animation that will show all the features discussed above. It should show the parabola which does not move, the movable point (0, a), the circle tangent to the parabola, z(x) and z’(x). These last 3 should move with the slider for a.

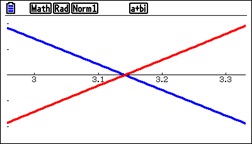
At this point I noticed that the derivative changed concavity 4 times (up-down-up-down). The origin is one of 3 points of inflection. I wondered if there was anything interesting about the location of the points of inflection.

Exercise 5: Find the coordinates of the points of inflection of z’(x). Are they related to any of the features in the problem? (Use a CAS for this one.)

The solutions can be found here: Closest Point Problem Solution.

Looking Ahead

Posted on by
3

Well the AP calculus exams are over. I hope all your students did well.

I’ll be cutting down the number of posts for the next few months. I will try to post once a week or so when I find something interesting. Remember if you click one of the RSS feeds or the “Follow this Blog” at the bottom of the right hand column you can get the postings without coming directly here.

In August I plan to go back to teaching high school for the first time in 15 years. I will be filling in for a friend who is going on sabbatical. That should be interesting and fun.

This blog was stared in August 2012 and I tried to do post on topics that would help a few weeks ahead of when I though most people would be teaching them. So you can go through the year monthly from the archives section on the right. Starting this coming August I hope to fill in the gaps from the first year by writing on topics I missed or expanding on the previous ones.

In the meanwhile, I’ll be working on the third edition of my book Teaching AP Calculus. I hope it will be out early next year.

Hope you have  relaxing and productive summer!