Category Archives: AP Calculus Exams

April

Posted on by
Reply

Update April 7, 2015: This video may have been more appropriate a week ago, but I had not seen it then.

 

 

Back to work: Review time  for the AP Exams is here. The AP Calculus exams this year are on Tuesday morning May 5, 2015. Most of you will be finishing your new work this month and getting ready to review. So I’m repeating most of my March 1 post here with the links to help you review. But first:

I’d like to invite you to the annual AP Calculus Panel Discussion and Reception at the NCTM Annual Meeting 

Date: Thursday April 16, 2014 from 6:00 PM to 8:00 PM

Location:

     Grand Ballroom Sections D/E 

     Westin Boston Waterfront Hotel,

     425 Summer Street, Boston, MA.  

The speakers will include

–          Stephen Kokoska, Chief Reader for Calculus

–          Vicki Carter – From the exam committee

–          Dennis Donovan – Question leader

–          Benjamin Hedrick – the College Board

–          Lin McMullin – moderator of the AP Calculus Community and host.  

After the panel discussion there will be a question and answer period, and a raffle.

Refreshments and adult beverages will be provided. The reception is free and no advance registration, conference registration, or RSVP is necessary. Just come, meet the panelists, and enjoy the discussion.

The reception is sponsored jointly by D & S Marketing System, Inc., Bedford, Freeman and Worth, and Hewlett-Packard.

As for reviewing: I suggest you review by topic spending 1 – 3 days on each type so that students can see the things that are asked for and the different ways they are asked. Most of the questions include topics taught at different times during the year; students are not used to this. By considering each type separately students will learn how to pull together what they have been studying all year.

Many of the same ideas are tested in smaller “chunks” on the multiple-choice sections, so looking at the type should help with not only free-response questions but many of the multiple-choice questions as well. You may also find multiple-choice questions for each of the types and assign a few of them along with the corresponding free-response type.

Ideas for Reviewing for the AP Calculus Exams

Calculator Use on the AP Exams (AB & BC)

Interpreting Graphs AP Type Questions 1

The Rate/Accumulation Question AP Type Question 2

Area and Volume Questions AP Type Question 3

Motion on a Line AP Type Question 4

The Table Question AP Type Question 5

Differential Equations AP Type Question 6

Implicit Relations and Related Rates AP Type Question 7 

Parametric and Vector Equations AP Type Question 8 (BC)

Polar Curves AP Type Question 9 (BC)

Sequences and Series AP Type Question 10 (BC)

Writing on the AP Calculus Exams

Posted on by
Reply

The goals of the AP Calculus program state that, “Students should be able to communicate mathematics and explain solutions to problems both verbally and in well written sentences.” For obvious reasons the verbal part cannot be tested on the exams; it is expected that you will do that in your class. The exams do require written answers to a number of questions. The number of points riding on written explanations on recent exams is summarized in the table below.

 Year AB BC
2007 9 9
2008 7 8
2009 7 3
2010 7 7
2011 7 6
2012 9 7
2013 9 7
2014 6 3

The average is between 6 and 8 points each year with some years having 9. That’s the equivalent of a full question. So this is something that should not be overlooked in teaching the course and in preparing for the exams. Start long before calculus; make writing part of the school’s math program.

That a written answer is expected is indicated by phrases such as:

  • Justify you answer
  • Explain your reasoning
  • Why?
  • Why not?
  • Give a reason for your answer
  • Explain the meaning of a definite integral in the context of the problem.
  • Explain the meaning of a derivative in the context of the problem.
  • Explain why an approximation overestimates or underestimates the actual value

How do you answer such a question? The short answer is to determine which theorem or definition applies and then show that the given situation specifically meets (or fails to meet) the hypotheses of the theorem or definition.

Explanations should be based on what is given in the problem or what the student has computed or derived from the given, and be based on a theorem or definition. Some more specific suggestions:

  • To show that a function is continuous show that the limit (or perhaps two one-sided limits) equals the value at the point. (See 2007 AB 6)
  • Increasing, decreasing, local extreme values, and concavity are all justified by reference to the function’s derivative. The table below shows what is required for the justifications. The items in the second column must be given (perhaps on a graph of the derivative) or must have been established by the student’s work.
Conclusion Establish that
y is increasing y’ > 0  (above the x-axis)
y is decreasing y’ < 0   (below the x-axis)
y has a local minimum y’ changes  – to + (crosses x-axis below to above) or {y}'=0\text{ and }{{y}'}'>0
y has a local maximum y’ changes + to –  (crosses x-axis above to below) or {y}'=0\text{ and }{{y}'}'<0
y is concave up y’ increasing  (going up to the right) or {{y}'}'>0
y is concave down y’ decreasing  (going down to the right) or {{y}'}'<0
y has point of inflection y’ extreme value  (high or low points) or {{y}'}' changes sign.
  •  Local extreme values may be justified by the First Derivative Test, the Second Derivative Test, or the Candidates’ Test. In each case the hypotheses must be shown to be true either in the given or by the student’s work.
  • Absolute Extreme Values may be justified by the same three tests (often the Candidates’ Test is the easiest), but here the student must consider the entire domain. This may be done (for a continuous function) by saying specifically that this is the only place where the derivative changes sign in the proper direction. (See the “quiz” below.)
  • Speed is increasing on intervals where the velocity and acceleration have the same sign; decreasing where they have different signs. (2013 AB 2 d)
  • To use the Mean Value Theorem state that the function is continuous and differentiable on the interval and show the computation of the slope between the endpoints of the interval. (2007 AB 3 b, 2103 AB3/BC3)
  • To use the Intermediate Value Theorem state that the function is continuous and show that the values at the endpoints bracket the value in question (2007 AB 3 a)
  • For L’Hôpital’s Rule state that the limit of the numerator and denominator are either both zero or both infinite. (2013 BC 5 a)
  • The meaning of a derivative should include the value and (1) what it is (the rate of change of …, velocity of …, slope of …), (2) the time it obtains this value, and (3) the units. (2012 AB1/BC1)
  • The meaning of a definite integral should include the value and (1) what the integral gives (amount, average value, change of position), (2) the units, and (3) what the limits of integration mean. One way of determining this is to remember the Fundamental Theorem of Calculus \displaystyle \int_{a}^{b}{{f}'\left( x \right)dx}=f\left( b \right)-f\left( a \right). The integral is the difference between whatever f represents at b and what it represents at a. (2009 AB 2 c, AB 3c, 2013 AB3/BC3 c)
  • To show that a theorem applies state and show that all its hypotheses are met. To show that a theorem does not apply show that at least one of the hypotheses is not true (be specific as to which one).
  • Overestimates or underestimates usually depend on the concavity between the two points used in the estimates.

A few other things to keep on mind:

  • Avoid pronouns. Pronouns need antecedents. “It’s increasing because it is positive on the interval” is not going to earn any points.
  • Avoid ambiguous references. Phrases such as “the graph”, “the derivative” , or “the slope” are unclear. When they see “the graph” readers are taught to ask “the graph of what?” Do not make them guess. Instead say “the graph of the derivative”, “the derivative of f”, or “the slope of the derivative.”
  • Answer the question. If the question is a yes or no question then say “yes” or “no.” Every year students write great explanations but never say whether they are justifying a “yes” or a “no.”
  • Don’t write too much. Usually a sentence or two is enough. If something extra is in the explanation and it is wrong, then the credit is not earned even though the rest of the explanation is great.

As always, look at the scoring standards from past exam and see how the justifications and explanations are worded. These make good templates for common justifications. Keep in mind that there are other correct ways to write the justifications.

QUIZ

Here is a quiz that can help your students learn how to write good explanations.

Let f\left( x \right)={{e}^{x}}\left( x-3 \right) for 0\le x\le 5. Find the location of the minimum value of f(x). Justify your answer three different ways (without reference to each other).

The minimum value occurs at x = 2. The three ways to justify this are the First Derivative Test, the Second Derivative Test and the Candidates’ Test. (Don’t tell your students what they are – they should know that.) Then compare and contrast the students’ answers. Let them discuss and criticize each other’s answers.

 

calculus

March

Posted on by
Reply

The AP Calculus exams this year are on Tuesday morning May 5, 2015. Most of you will be finishing your new work this month and getting ready to review. As usual I like to stay a little ahead of where you are so you have time to consider what is offered here.

To help you plan ahead, below are links to previous posts specifically on reviewing for the AP Calculus exams and on the type questions that appear on the free-response sections of the exams.

I suggest you review by topic spending 1 – 3 days on each type so that students can see the things that are asked for and the different ways they are asked. Most of the questions include topics taught at different times during the year; students are not used to this. By considering each type separately students will learn how to pull together what they have been studying all year.

Many of the same ideas are tested in smaller “chunks” on the multiple-choice sections, so looking at the type should help with not only free-response questions but many of the multiple-choice questions as well. You may also find multiple-choice questions for each of the types and assign a few of them along with the corresponding free-response type.

Ideas for Reviewing for the AP Calculus Exams

Calculator Use on the AP Exams (AB & BC)

Interpreting Graphs AP Type Questions 1  chalkboard_math_notes

The Rate/Accumulation Question AP Type Question 2

Area and Volume Questions AP Type Question 3

Motion on a Line AP Type Question 4

The Table Question AP Type Question 5

Differential Equations AP Type Question 6

Implicit Relations and Related Rates AP Type Question 7 

Parametric and Vector Equations AP Type Question 8 (BC)

Polar Curves AP Type Question 9 (BC)

Sequences and Series AP Type Question 10 (BC)

I’ll be traveling this month to do some workshops and will not be posting too much new until I return.

Mean Tables

Posted on by
Reply

The AP calculus exams always seem to have a multiple-choice table question in which the stem describes function in words and students are asked which of 5, now 4, tables could be a table of values for the function.  Could be because you can never be sure without other information what happens between values in the table. So, the way to solve the problem is to eliminate choices that are at odds with the description.

The question style nicely makes students relate a verbal description with the numerical information in the tables. This uses two parts of the Rule of Four.

In 2003, question AB 90 told students that a function f had a positive first derivative and a negative second derivative on the closed interval [2, 5]. There were five tables to choose from.

There is a fairly quick way to solve the problem, but I want to go a little slower and discuss the theorems that apply.

First, since the function has first and second derivatives on the interval, the function and its first derivative are continuous on the interval. This is important since, if they were not continuous, there would be no way to solve the problem.

Next, since the first derivative is positive, the function must be increasing. This allowed students to quickly eliminate three choices where the function was obviously decreasing. The remaining tables showed increasing values and thus could not be eliminated based on the first derivative.

The two remaining tables were

Table MVT

Notice that in table A the values are increasing at an increasing rate, and in table B the values are increasing at a decreasing rate. Thus, table B is the correct choice. By the end of the year that kind of reasoning is enough for students to determine the correct answer.

Students could also draw a quick graph and see that table A was concave up and B was concave down. This will give them the correct answer, but technically it is a wrong approach since, once again, there is no way to know what happens between the values; we should not just connect the points and draw a conclusion.

The correct reasoning is based on the Mean Value Theorem (MVT).

In table A, by the MVT there must be a number c1 between 2 and 3 where {f}'\left( {{c}_{1}} \right)=2 the slope between the points (2,7) and (3, 9). Also, there must be a number c2 between 3 and 4 where {f}'\left( {{c}_{2}} \right)=3 the slope between (3, 9) and (4, 12), and likewise a number c3 between 4 and 5 where {f}'\left( {{c}_{3}} \right)=4.

Then applying the MVT to these values of {f}'\left( x \right), there must be a number, say d1 between c1 and c2 where {{f}'}'\left( {{d}_{1}} \right)=\frac{3-2}{{{c}_{2}}-{{c}_{1}}}>0. Since the second derivative should be negative everywhere, table A is eliminated making the remaining table B the correct choice.

If we do a similar analysis of Table B, we find that the MVT values for the second derivative are all negative. However, we cannot be sure this is true for all values of f in table B, since we can never be sure what happens between the values in a table. But table B is the only one that could be the one described since the others clearly are not.

In this post we saw how the MVT can be used in a numerical setting. I discussed the MVT in an analytic setting on September 28, 2012 and graphically on October 1, 2012.

Darboux’s Theorem

Posted on by
1
Jean Gaston Darboux 1842 - 1917

Jean Gaston Darboux
1842 – 1917

Jean Gaston Darboux was a French mathematician who lived from 1842 to 1917. Of his several important theorems the one we will consider says that the derivative of a function has the Intermediate Value Theorem property – that is, the derivative takes on all the values between the values of the derivative at the endpoints of the interval under consideration.

Darboux’s Theorem is easy to understand and prove but is not usually included in a first-year calculus course (and is not included on the AP exams). Its use is in the more detailed study of functions in a real analysis course.

You may want to use this as an enrichment topic in your calculus course, or a topic for a little deeper investigation. The ideas here are certainly within the range of what first-year calculus students should be able to follow. They relate closely to the Mean Value Theorem (MVT). I will suggest some ideas (in blue) to consider along the way.

More precisely Darboux’s theorem says that

If f is differentiable on the closed interval [a, b] and r is any number between f ’ (a) and f ’ (b), then there exists a number c in the open interval (a, b) such that f ‘ (c) = r. 

Differentiable on a closed interval?

Most theorems in beginning calculus require only that the function be differentiable on an open interval. Here, obviously, we need a closed interval so that there will be values of the derivative for r to be between.

The limit definition of derivative requires a regular two-sided limit to exist; at the endpoint of an interval there is only one side. For most theorems this is enough. Here the definition of derivative must be extended to allow one-sided limits as x approaches the endpoint values from inside the interval. Also note that  if a function is differentiable on (a, b), then it is differentiable on any closed sub-interval of (a, b) that does not include a or b.

Geometric proof [1]

Consider the diagram below, which shows a function in blue. At each endpoint draw a line with the slope of r. Notice that these two lines have a slope less than that of the function at the left end and greater than the slope at the right end. At least one of these lines must intersect the function at an interior point of the interval.  Before reading on, see if you and your students can complete the proof from here. (Hint: What theorem does the top half of the figure remind you of?)

DarbouxOn the interval between the intersection point and the end point we can apply the Mean Value Theorem and determine the value of c where the tangent line will be parallel to the line through the endpoint. At this point f ‘(c) = r. Q.E.D.

Analytic Proof [2]

Consider the function h\left( x \right)=f\left( x \right)-(f(b)+r(x-b)). Since f(x) is differentiable, it is continuous; \displaystyle f(b)+r(x-a) is also continuous and differentiable. Therefore, h(x) is continuous and differentiable on [a, b]. By the Extreme Value Theorem, there must be a point, x = c, in the open interval (a, b) where h(x) has an extreme value. At this point h’ (c) = 0.

Before reading on see if you can complete the proof from here.

\displaystyle h(x)=f(x)-(f(b)+r(x-a))

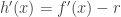
\displaystyle {h}'(x)={f}'(x)-r

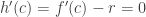
\displaystyle {h}'(c)={f}'(c)-r=0

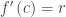
\displaystyle {f}'\left( c \right)=r

Q.E.D.

Exercise: Compare and contrast the two proofs.

  1. In the geometric proof, what does \displaystyle y=f(b)+r(x-a) represent? Where does it show up in the diagram?
  2. How do both proofs relate to the Mean Value Theorem (or Rolle’s Theorem).

The function \displaystyle h(x)=f(x)-(f(b)+r(x-a)) represents the vertical distance from f(x) to \displaystyle f(b)+r(x-a). In the diagram, this is a vertical segment connecting f(x) to  \displaystyle y=f(b)+r(x-a).This expression may be positive, negative, or zero. In the diagram, at the point(s) where the line through the right endpoint intersects the curve and at the endpoint h(x) = 0. Therefore, h(x) meets the hypotheses of Rolle’s Theorem (and the MVT), and the result follows.

The line through the right endpoint will have equation the y=f(b)+r(x-b) This makes h\left( x \right)=f\left( x \right)-\left( f(b)+r(x-b) \right). When differentiated and the result will be {f}'\left( x \right)-r the same expression as in the analytic proof.

Also, you may move this line upwards parallel to its original position and eventually it will be tangent to the graph of the function. (See my posts on MVT 1 and especially MVT 2).

Exercise:

Consider the function f(x) = sin(x)

  1. On the interval [1,3] what values of the derivative of f are guaranteed by Darboux’s Theorem? .
  2. Does Darboux’s theorem guarantee any value on the interval [0,2\pi ]? Why or why not?

Answers:

  1. f ‘(x) = cos(x). f ‘ (1) = 0.54030 and f ‘ (3) = -0.98999. So the guaranteed values are from -0.98999 to 0.54030.
  2. No. f ‘ (x) = 1 at both endpoints, so there are no values between one and one.

Another interesting aspect of Darboux’s Theorem is that there is no requirement that the derivative f ‘(x) be continuous!

A common example of such a function is

\displaystyle f\left( x \right)=\left\{ \begin{matrix} {{x}^{2}}\sin \left( \frac{1}{x} \right) & x\ne 0 \\ 0 & x=0 \\ \end{matrix} \right.

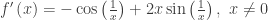With \displaystyle {f}'\left( x \right)=-\cos \left( \tfrac{1}{x} \right)+2x\sin \left( \tfrac{1}{x} \right),\,\,x\ne 0.

This function (which has appeared on the AP exams) is differentiable (and therefore continuous).There is an oscillating discontinuity at the origin. The derivative is not continuous at the origin.  Yet, every interval containing the origin as an interior point meets the conditions of Darboux’s Theorem, so the derivative while not continuous has the intermediate value property.

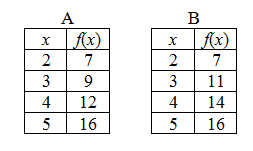
AP exam question 1999 AB3/BC3 part c:

Finally, what inspired this post was a recent discussion on the AP Calculus Community bulletin board about the AP exam question 1999 AB3/BC3 part c. This question gave a table of values for the rate, R, at which water was flowing out of a pipe as a differentiable function of time t. The question asked if there was a time when R’ (t) = 0. It was expected that students would use Rolle’s Theorem or the MVT. There was a discussion about using Darboux’s theorem or saying something like the derivative increased (or was positive), then decreased (was negative) so somewhere the derivative must be zero (implying that derivative had the intermediate value property). Luckily, no one tried this approach, so it was a moot point.

Take a look at the problem with your students and see if you can use Darboux’s theorem. Be sure the hypotheses are met.

Answer (try it yourself before reading on):

The function is not differentiable at the endpoints. But consider an interval like [0,3]. Using the given values in the table, by the MVT there is a time t = c where R‘(c) = 0.8/3 > 0, and there is a time t = d on the interval [21, 24] where R‘(d) = -0.6/3 < 0. The function is differentiable on the closed interval [c, d] so by Darboux’s Theorem there must exist a time when R’(t) = 0. Admittedly, this is a bit of overkill.

References:

  1. After Nitecki, Zbigniew H. Calculus Deconstructed A Second Course in First-Year Calculus, ©2009, The Mathematical Association of America, ISBN 978-0-883835-756-4, p. 221-222.
  2. After Dunham, William The Calculus Gallery Masterpieces from Newton to Lebesque, © 2005, Princeton University Press, ISBN 978-0-691-09565-3, p. 156.

Both these book are good reference books.

Updated: August 20, 2014, and October 4, 2017

Pacing for AP Calculus

Posted on by
9

Some thoughts on pacing and planning your year’s work for AP Calculus AB or BC.  The ideas are my own and are only suggestions for you to consider.

Almost all textbooks provide an AP pacing guide among their ancillary material. You can consult the guide for your book for specific suggestions for the number of days on each topic or section.

Keep a copy of the latest Course and Exam Description handy. Changes in the exam are announced in this book; to keep up to date be sure you always read the following year’s edition which is available at AP Central shortly after the exam is given in May. The book contains the “Topical Outline” for the AB and BC courses. The topics listed here are what may be tested on the exams. What is not listed will not be tested. For example, calculating volumes by the method of Cylindrical Shells is not listed; any volume problem on the exam can be done by other methods. This does not mean you may not or should not teach the topics that are not listed if you believe your students will benefit from them. If you wish to teach them you may still do so. Students may use these methods on the exam; they will not be penalized for correct mathematics. Many teachers teach these topics in the time after the exam.

PLANNING YOUR YEAR

Get out your school calendar. The AP Calculus exams are usually given during the first week in May; the exact date will be at AP Central.

  • Count back about 2 school weeks from the exam date (don’t count your spring break week). Allow an extra week if you are prone to many snow days. This time will be used for review. (This brings you to a week or so into April.)
  • Count back two more weeks. I’ll discuss what this should time should be used for later. (Mid-march) This is when you should aim to be done the material and ready to begin review. Finishing by the beginning of March is even better.
  • Count the number of weeks between the beginning of school and the week above. (About 26 – 27 weeks if your start just after Labor Day; 28-30 weeks if you start in mid-August). This is the number of week you have to teach the material. Don’t panic: the AB course is taught typically in college in 30 – 35 classes in one semester. You do have time, but by the same token, you still need to stick with the calendar and keep you students on it as well.
  • Take half of this number and find the middle week of the year. This is sometime in early to mid-December. To allow equal time for derivatives and integrals, this is when you should finish derivatives and start integration. Don’t delay starting integration beyond the first class of the New Year.
  • Now plan your work so that you can do it in the time allowed. You all want your students to do well. It is not unknown for teachers to spend a few extra days now and then to give extra work on derivative. But this time adds up. Remember half the exam is integration; you need to cover that too. Don’t get behind.
  • If you are in an area where there are closings due to weather or other reasons, plan for them. You usually get some short warning that snow is coming. Be ready on short notice to post an assignment, a video to watch, or some other useful work on your website. If it looks like several days off, tell the students you will post the assignment daily and make them responsible for finding them and doing them.

Look over past exams. Learn what is tested and how it is tested and plan your time accordingly. Here are some hints as to where you can shave some time.

STARTING THE YEAR

  • Summer assignments: Personally, I do not see the use in summer assignments. What is their purpose? To keep the material fresh in the kids’ minds, I suppose. But the good students will do it right away and then forget anyway over the summer, and the others, will forget “everything” over the summer and try the assignment at the end of the summer and get nowhere.
  • If you want to keep their minds on mathematics over the summer, assign a good book to read. Maybe they will spread that out over the summer. Reading suggestion: Is God a Mathematician? by Mario Livio.
  • Ideally, limits and continuity should be taught in pre-calculus. Work with your pre-calculus teachers and help them arrange their curriculum so that the things students need to know coming into calculus are taught in pre-calculus. This is one of the things vertical teaming can accomplish. (Incidentally, be sure they do not start learning about derivatives and the slope of tangent lines in pre-calculus as some textbooks do; the time is better spent elsewhere.) Remember the delta-epsilon definition is not tested and is optional.
  • DO NOT begin the year with a week or two (or even a day or two) of review of mathematics up to calculus. It won’t help. Later in the year when you get to one of those topics students “should” know, they will have forgotten it all over again. So instead of a week or two (or more) of review at the beginning of the year, plan 10 – 15 minutes of review when these topics come up during the year. (You’ll have to do this anyway.)
  • If the first chapter of your textbook is review, as most are, skip this chapter. Make your first night’s assignment to read this chapter and ask about anything they don’t remember. This chapter can be used for reference when necessary later in the year.
  • Do begin the year with derivatives (or limits and continuity if students have not studied this before). The very fact that this is new will help get and retain the students’ interest.

DERIVATIVES

Here are some places you may shave a few days off while teaching derivatives:

  • Computing derivatives is important. Product rule, Quotient rule, Chain rule are all tested on the exam. But look at some past exams: the questions are not that complicated. It is rare to find “monster” problems involving all three rules together along with radicals and trig functions. Sure, give one or two of those, but the basics are what are tested. Furthermore, you can and should include these all thru the year, so students stay in practice.
  • Optimization problems: Building a cheaper box or fencing in the largest field with a given amount of fence are great problems. They do not appear on the AP exams (at least not since 1982). They do not appear because the hard part is writing the model (the equation); if a student misses this they cannot earn anymore points in the problem. If these problems were on the exam, missing the equation means the student could not go on and cost the student all 9 points on a free-response question. Finding maximums and minimum, which require the same calculus thinking and techniques, are tested in other ways. On the multiple-choice section, optimization questions, if any, are of the easiest sort. The model may even be given, and there will  be no more than one such question. Spend only a day or two on the modeling.
  • Related Rate problems: These questions do appear on the exams. A multiple-choice question on related rates may appear. As with any multiple-choice question it cannot be too difficult. Every few years a related rate question shows as part of a free-response question. You cannot cut this out completely, but you can shave some time off here if you are short of time.
  • Practice the differentiation skills, and later the antidifferentiation skills, and the concepts associated with derivatives by including them on all your tests. Make all tests cumulative from the beginning of the year; just a random question or two will keep them on their toes.
  • Look for and assign differentiation problems based on graphs and tables of values in addition to the usual analytic (equation) questions. Use your textbook; however, some textbooks are rather thin on questions with tables and graphs in the stem. Use released exams or a review book for sources.

INTEGRALS

  • As with derivatives, the finding of antiderivatives is important, but the antiderivatives, definite and indefinite integrals are not very difficult. There are no trig substitution integrals, and nothing too monstrous. Integration by Parts is only on the BC exam.  Give students lots of practice spread over the second half of the year.
  • Trapezoidal Rule is not really tested on the exams. Students do not need to know the formula or the error bound formula for the Trapezoidal Rule. Questions do ask for a “trapezoidal approximation.” Like the left-, right; and midpoint-Riemann sums approximations, these questions can be answered by actually drawing a small number of trapezoids and computing their areas. This should be done from equations, graphs and tables. This tests the concept and often the graphical interpretation, not the mindless use of a formula. Error analysis is tested based on whether the approximating rectangles or trapezoids lie above or below the graph. Simpson’s Rule is not tested.
  • Look for and assign integration problems based on graphs and tables of values in addition to the usual analytic (equation) questions. Use your textbook, released exams or a review book for sources.

THOSE TWO WEEKS BEFORE THE REVIEW STARTS

The free-response and the multiple-choice sections of the exam contain some questions very similar to questions that are in textbooks and in contiguous sections of the textbook. These include:

The free-response and the multiple-choice sections contain some questions that are very different from questions that are in textbooks. This is because these questions are on topics from different parts of the year (limit, differentiation and integration concepts in the same question), and these questions are just not asked in the same way in textbooks. These include:

  • Rate/accumulation questions
  • Graph Analysis Differentiation and integration questions about a function given the graph of its derivative and functions defined by integrals
  • Motion on a line (AB), or motion in a plane (BC – parametric and vector equations)
  • Polar Equations (BC only)
  • Questions, both differentiation and integration, given a table of values.
  • Overlapping topics in the same question such as a particle motion question based on a graph or table stem, or a question about an important theorem based on value in a table.

The topics in this latter list pull the entire year’s work together. At first students find this disconcerting since they have rarely seen questions like these; so be sure they do see them before the test. Use these two weeks to pull these topics together and get your students thinking more broadly. This will lead naturally into the full-scale review; in fact, some of this work may profitably spill over into the review time.  Spend 2 – 3 days on each type using actual AP questions for each so the students can see the different variations on the same idea, and the different ways the same idea can be tested. (This is preferable starting the review with one complete free-response exam with 6 different type questions to do. However, later in the review you should do this.)

Another way to approach these problems is to include parts of them throughout the year as the students learn the topics tested in each part. Released multiple-choice problems can be used for this purpose as well.

THE REVIEW TIME

Once the students are familiar with the style of questions, give them a mock exam. For the multiple-choice questions use one of the released exams or one of the genuine-fake exams in a good review book. Give the free-response questions from a recent year. If possible, give the mock exam under the same conditions and timing as the exam. This can be done on a Saturday. If you cannot get 3.25 hours in a row, then give the parts with their proper timing during class periods. Grade the exam according to the standards which are available at AP Central.  Teach them some good test taking strategies.

Spend a fair amount of time doing multiple-choice questions. The released exams from 1998, 2003 and 2008, 2012 and 2013 (and soon 2014) are available. You can also use questions from a good review book (AB or BC). Pay attention to the style and wording, as well as the concepts tested.

Make your calendar up in advance and stick to it. You won’t help the students by getting behind; in college they will have to go a lot faster than in high school. Help them get used to it.

I hope this helps you get started and keep a proper pace through the year.

Revised and updated June 6, 2021

“Easier” Exams

Posted on by
Reply

There were two questions posted recently on the AP Calculus Community bulletin board. One teacher was concerned that his students took two different forms of the Calculus exam, and the means were not the same. He felt that one group has an easier time than the other. The other writer noted that on his (physics) exam three questions were not counted – there appeared to be only 32 questions instead of the 35 he expected.

My answer, which you may be interested in, was:

It is impossible to make two forms of the same test of equal difficulty. I repeat: It is impossible to make two forms of the same test of equal difficulty. (And if the two forms are equal in difficulty, it is due more to dumb luck than good management.)

What the ETS (Educational Testing Service) does to account for this fact is to adjust the cut points for the scores (5-4-3-2-1). A form of the exam that is “easier”, in the sense of having higher overall means, also has higher cut points. Regardless of the difficulty of the form of the exam the score (5-4-3-2-1) reflects the same amount of knowledge of the subject (as best as possible). Any other scheme would certainly not be fair. So, there is no need to be concerned that someone else had an easier exam than your students. They may well have, but their and your students’ score (5-4-3-2-1) reflects the same knowledge. Your students, and those with the easier exam, will get the score they earned.

Then I suggested that he consider his students one at a time without regard to the form of the test they took. Check and see if the students got the score you expected them to get. Keeping in mind that students often surprise or disappoint us, did the students get the scores he anticipated. If, in general, they got the scores he expected without regard to the form, then the ETS did its job.

As to the second concern: The ETS looks at the results individually for each and every question on the exam. If everyone scores very low on a particular question, or if some identifiable sub-group (men, women, one or more minorities) has scores that are way out of line with everyone else, the question is rejected and not scored. The other scores are re-weighted accordingly and the final score (5-4-3-2-1) reflects the same knowledge of the subject. This happens in math and science, but I suspect it happens more often in history, English, and the social sciences.

You might also refer to my recent post of May 12, 2014 Percentages Don’t Make the Grade on this topic.

Updated and revised July 12, 2014.