Who’d a thunk it?

Posted on July 18, 2017 by Lin McMullin

Cubic Symmetry

Some things are fairly obvious. For example, if you look at the graphs of a few cubic equations, you might think that each is symmetric to a point and on closer inspection the point of symmetry is the point of inflection.

This is true and easy to prove. You can find the point of inflection, and then show that any point a certain distance horizontally on one side is the same distance above (or below) the point of inflection as a point the same distance horizontally on the other side is below (or above). Another way is to translate the cubic so that the point of inflection is at the origin and then show the resulting function is an odd function (i.e. symmetric to the origin).

But some other properties are not at all obvious. How someone thought to look for them is not even clear.

Tangent Line.

If you have cubic function with real roots of x = a, x = b, and x = c not necessarily distinct, if you draw a tangent line at a point where x is the average of any two roots, x = ½(a + b), , then this tangent line intersects the cubic on the x-axis at exactly the third root, x = c. Here is a Desmos graph illustrating this idea.

Here is a proof done with a CAS. The first line is a cubic expressed in terms of its roots. The third line asks where the tangent line at x = m intersects the x-axis. The last line is the answer: x = c or whenever a = b (i.e. when the two roots are the same, in which case the tangent line is the x-axis and of course also contains x = c.

Areas
Even harder to believe is this: Draw a tangent line anywhere on a cubic. This tangent will intersect the cubic at a second point and the line and the cubic will define a region whose area is A1. From the second point draw a tangent what intersects the cubic at a third point and defines a region whose area is A2. The ratio of the areas A2/A1 = 16. I have no idea why this should be so, but it is.

Here is a proof, again by CAS: The last line marked with a square bullet is the computation of the ratio and the answer, 16, is in the lower right,

And if that’s not strange enough, inserting two vertical lines defines other regions whose areas are in the ratios shown in the figure below.

Who’d a thunk it?

Synthetic Summer Fun

Posted on July 10, 2017 by Lin McMullin

Today, for some summer fun, let’s look at synthetic division a/k/a synthetic substitution. I’ll assume you all know how to do that since it is a pretty common pre-calculus topic and even comes up again in calculus.

Why Does Synthetic Division Work?

An example: consider the polynomial

$P(x)=2{{x}^{4}}-3{{x}^{3}}-11{{x}^{2}}+14x-1$ .

This can be written in nested form like this

$P(x)=((((2x-3)x-11)x+14)x-1)$

To evaluate this last expression at, say x = 2, we do the arithmetic as follows:

2 x 2 – 3 = 1
2 x 1 – 11 = –9
2 x (–9) + 14 = –4
2 x (–4) – 1 = – 9 = f(2)

Notice that this requires only multiplication and addition or subtraction, no raising to powers. More to the point, this is the same arithmetic, in the same order when you do the evaluation by synthetic division, and the work is a little easier to keep track of.

$\begin{matrix} {} & 2 & -3 & -11 & 14 & -1 \\ 2) & 2 & 1 & -9 & -4 & -9 \\ \end{matrix}\begin{matrix} {} \\ \,=P(2) \\ \end{matrix}$

Synthetic division has another advantage: the other numbers in the second row are the coefficients of a quotient polynomial, a polynomial of one less degree that the original. So,

$\displaystyle \frac{P(x)}{x-2}=2{{x}^{3}}+{{x}^{2}}-9x-4+\frac{-9}{x-2}$

The Remainder Theorem and the Factor Theorem

In general, a polynomial of degree n, divided by a linear factor (x – a) gives a polynomial Q(x) of degree n – 1 and a remainder R

$\displaystyle \frac{P(x)}{x-a}=Q(x)+\frac{R}{x-a}$

$P(x)=Q(x)(x-a)+R$

From here it is easy to see that $P(a)=R$ . This is called the remainder theorem. It has a corollary called the factor theorem: If R = 0, then (x – a) is a factor of P(x).

Calculus

But wait there is more: differentiating the equation above using the product rule gives

${P}'(x)=Q(x)(1)+Q(x)(x-a)+0$ and substituting x = a gives

${P}'(a)=Q(a)$ . The value of the quotient polynomial at a is the derivative of the original polynomial at a.

Of course, we could also rewrite the same equation as $\displaystyle \frac{P(x)-P(a)}{x-a}=Q(x)$ . Then

$\displaystyle {P}'(a)=\underset{x\to a}{\mathop{\lim }}\,\frac{P(x)-P(a)}{x-a}=\underset{x\to a}{\mathop{\lim }}\,Q(x)=Q(a)$

Taylor Series

But wait, there’s even more.

A polynomial is a Maclaurin series in which all the terms after the n^th term are zero. When you students are first learning how to write a Taylor series, by finding all the derivatives and substituting in the general term, a good exercise is to have them write the Taylor series for a polynomial centered away from the origin. For the example above:

$P(x)=-9-2\left( x-2 \right)+19{{\left( x-2 \right)}^{2}}+13{{\left( x-2 \right)}^{3}}+2{{\left( x-2 \right)}^{4}}$

Then ask them to expand the expression above and collect term etc. They should get the original polynomial again (and have some great practice expand powers of a binomial).

Can synthetic division help us? Yes, of course. Here, is the original computation again:

$\begin{matrix} {} & 2 & -3 & -11 & 14 & -1 \\ 2) & 2 & 1 & -9 & -4 & -9 \\ \end{matrix}\begin{matrix} {} \\ \,=P(2) \\ \end{matrix}$

If we ignore the –9 and divide the quotient numbers by 2 we get

$\begin{matrix} {} & 2 & 1 & -9 & -4 \\ 2) & 2 & 5 & 1 & -2 \\ \end{matrix}\begin{matrix} {} \\ \ ={P}'(2) \\ \end{matrix}$

$\begin{matrix} {} & 2 & 5 & 1 \\ 2) & 2 & 9 & 19 \\ \end{matrix}\begin{matrix} {} \\ \ =\frac{{{P}'}'(2)}{2} \\ \end{matrix}$

And again

$\begin{matrix} {} & 2 & 9 \\ 2) & 2 & 13 \\ \end{matrix}\begin{matrix} {} \\ \ =\frac{{{{P}'}'}'\left( 2 \right)}{3!} \\ \end{matrix}$

One more time

$\begin{matrix} {} & 2 \\ 2) & 2 \\ \end{matrix}\begin{matrix} {} \\ \ =\frac{{{P}^{(4)}}\left( 2 \right)}{4!} \\ \end{matrix}$

What do you see? Right, the last numbers in each computation, –9, –2, 19, 13, and 2, are the coefficients of the Taylor polynomial!

If you really want to dive this home and have some more summer fun here’s the start of a proof (at least for n = 4). Let

$P(x)={{c}_{4}}{{x}^{4}}+{{c}_{3}}{{x}^{3}}+{{c}_{2}}{{x}^{3}}+{{c}_{1}}x+{{c}_{0}}$ and divide this by a:

$\begin{matrix} {} & {{c}_{4}} & {{c}_{3}} & {{c}_{2}} & {{c}_{1}} & {{c}_{0}} \\ a) & {{c}_{4}} & {{c}_{4}}a+{{c}_{3}} & {{c}_{4}}{{a}^{2}}{{+}_{{}}}{{c}_{3}}a+{{c}_{2}} & {{c}_{4}}{{a}^{3}}+{{c}_{3}}{{a}^{2}}+{{c}_{a}}a+{{c}_{1}} & {{c}_{4}}{{a}^{4}}+{{c}_{3}}{{a}^{3}}+{{c}_{a}}{{a}^{2}}+{{c}_{1}}a+{{c}_{0}}=P(a) \\ \end{matrix}$

Again

$\begin{matrix} {} & {{c}_{4}} & {{c}_{4}}a+{{c}_{3}} & {{c}_{4}}{{a}^{2}}{{+}_{{}}}{{c}_{3}}a+{{c}_{2}} & {{c}_{4}}{{a}^{3}}+{{c}_{3}}{{a}^{2}}+{{c}_{2}}a+{{c}_{1}} \\ a) & {{c}_{4}} & 2{{c}_{4}}a+{{c}_{3}} & 3{{c}_{4}}{{a}^{2}}+2{{c}_{3}}a+{{c}_{2}} & 4{{c}_{4}}{{a}^{3}}+3{{c}_{3}}{{a}^{2}}+2{{c}_{2}}a+{{c}_{1}} \\ \end{matrix}\begin{matrix} {} \\ \ ={P}'(a) \\ \end{matrix}$

And I’ll leave the rest to you. Really, why should I have all the fun?

Exams or Vacation?

Posted on April 14, 2017 by Lin McMullin

What are you looking forward to most: the exam or April vacation?

As I’ve mentioned before, I try to keep my posts a little ahead of where I assume you are. With the exams in less than a month away, this means I’m about done for this year. I’m now going to take some time off from posting every week.

The posts on reviewing for the exams have been posted. You may find them by scrolling down the first page on under the “Thru the Year” tab at the top where they will be from now on. There will be a few posts over the summer, and I’ll start on a regular basis around the beginning of August.

You can receive an email whenever I write a new post by clicking on the RSS-Post and or RSS-Comments link in the column on the right side. If you have and questions or suggestions about what you would like me to write about please email me at lnmcmulin@aol.com .

Thanks for reading this year. Enjoy your vacation and Good Luck on the exam.

NCTM Calculus Panel Notes

Posted on April 11, 2017 by Lin McMullin

This past week I attended the NCTM Annual Meeting in San Antonio, Texas. For many years now, the sessions included a panel discussion on AP Calculus. This year Stephen Davis, chief reader for AP Calculus, was the principal speaker. I would like to share a few of his comments and insights some of which may help your students on the upcoming exams.

One of the things I recommend in preparing your students for the exam is to go over the directions to both parts of the exam. You should especially explain the three-decimal place rule and the (non-) simplification policy.

This year there will be a slight change in the free-response directions. This change is not a policy change; the change in the wording was made to emphasize what has been the policy for some years. Here is the new wording of the first bullet of the free-response directions with the changes underlined:

Show all your work, even though a question may not explicitly remind you to do so. Clearly label any functions graphs, tables, or other objects that you use. Justifications require that you give mathematical reasons, and that you verify the needed conditions under which relevant theorems, properties, definitions, or tests are applied. Your work will be scored on the correctness and completeness of your methods as well as your answers. Answers without supporting work will usually not receive credit.

For an example of the first underlining sentence, consider 2016 AB 2. This is a linear motion (Type 2) question. Part (a) asks “At time t = 4, is the particle speeding up or slowing down?” According to the scoring standards, two points could be earned for “conclusion with reason.” This means that a correct conclusion of “slowing down” received no credit, because no work was shown. Correct work includes the computation of the velocity and acceleration at t = 4 and indication they since they have different signs the particle is slowing down.

In the same exam, 2016 BC 4 (c) illustrates the second underlined sentence above. This was a L’Hôpital’s Rule question. Just writing

$\displaystyle \underset{x\to -1}{\mathop{\lim }}\,\left( \frac{g\left( x \right)-2}{3{{\left( x+1 \right)}^{2}}} \right)=\underset{x\to -1}{\mathop{\lim }}\,\left( \frac{{g}'\left( x \right)}{6\left( x+1 \right)} \right)=-\frac{1}{3}$

does not earn the point. Students must indicate that they are using L’Hôpital’s Rule preferably by stating that the limits of the numerators and denominators at each stage are zero.

Another example from 2016 AB 3/BC 3 (Type 3): This problem showed the graph of a function f and asked about the function g defined as $g\left( x \right)=\int_{2}^{x}{f\left( t \right)dt}$ . Students were required to specifically state that ${g}'\left( x \right)=f\left( x \right)$ somewhere, somehow, in some part of the question, showing that they understood the relationship implied by the Fundamental Theorem of Calculus.

People started asking questions of the kind they ask on the AP Calculus Community Bulletin Board. They are “what if” questions: What if a student forgets the dx? What if the student gives open intervals and they should be closed? What if they use the x as the upper limit of integration and in the integrand? What if …? What if …?

Here is a comment I wrote a few days ago for the Community Bulletin board that Stephen was kind enough to mention:

I am sure you teach your students to do the problems correctly, use proper notation, and, even though this is not an English exam, to spell things correctly. You may deduct points in your class for failing to do any of that, or constantly remind them.

As others have pointed out, the readers do their best to give kids the credit they earn and there are not enough points to go around for some mistakes. The procedures for dx and missing parentheses etc. are not something you even need to tell or even mention to your students. Why would you? In scoring the mock exams take off when they make these mistakes. The mock exams should be a little harder than the real thing – that will only help the kids.

To answer your question: students will get full credit on the exams if they do everything right, and sometimes with a little less than everything right. Don’t show your students the minimum they can get away with. They don’t need to know that and it does not help them.

The exceptions are the algebraic and numerical simplifying rules and the three or more-decimal place rule.

A Logistics Graph???

Stephen included slide above in his presentation. It shows the growth in the number of students taking the AP Calculus exams since they first stared in 1956. The AB/BC split first happened in 1969. For years, we have been looking at what looked like exponential growth knowing this wasn’t possible. This kind of growth surely must be logistic since there is an upper limit to the number of students who could take the exam, namely the number of kids in high school.

So, have we reached the point where the numbers start to level off? Or is this just a slight pause such as happened around 1989 and again around 1995? Stay tuned.

Domain of a Differential Equation

Posted on April 7, 2017 by Lin McMullin

A reader recently asked me to do a post answering some questions about differential equations:

The 2016 AP Calculus course description now includes a new statement about domain restrictions for the solutions of differential equations. Specifically, EK 3.5A3 states “Solutions to differential equations may be subject to domain restrictions.” [The current 2020 CED uses the same wording in Essential Knowledge statement FUN-7.E.3] Could you write a blog post discussing (1) an example of how to determine the domain restriction; (2) speculating on whether one of the points for the differential equation on the free response will be allotted for specifying the restriction; and (3) speculating whether this concept could appear on the multiple choice and if so how.

First, let me compliment him on noticing EK 3.5A3. I overlooked it and have not seen anyone pick up on this yet. It seems to be a new item in the course description. Don’t panic. In the current 2020 CED EK FUN-7.E.3 says

A single question asking for the domain and range was asked before, but some time ago. Specifically, 2000 AB6 and 2006 AB 5 asked for the domain of the solution of a differential equation (see below for both). These are the only instances I can find that required students to find the domain of the solution.

Since 2008 many of the scoring standards included the domain, but they were not required to earn any points. These are discussed below. The domains were included in the solution, I suspect, because the standards are made public, and the readers want to publish the most complete answer.

What is required of the domain?

The generally accepted requirements are that the solution of a differential equation must be a function whose domain (1) must be an open interval, (2) on which the differential equation is true, and (3) contains the initial condition. Comments:

The interval must be open since derivatives are not defined at the endpoints of intervals. The derivative is a two-sided limit and at an endpoint you can only approach from one side. While one-sided derivatives may be defined, they are a more burdensome requirement and not necessary.
Practically speaking, this means that the solution may not cross a vertical asymptote or go through a point where the function is undefined; it must stay on the side where the initial condition is.
The differential equation must be true in the sense that substituting the solution and its derivative(s) into the differential equation must result in an identity. (See 2007 AB 4(b) for practice).
And of course, the initial condition point’s x-coordinate must be in the domain.

Teachers sometimes ask why we cannot just skip over an asymptote or an undefined point. When you do this, you are then working with a piecewise function. No problems there, but consider that on the piece(s) outside the domain as described above, you could have any function you want and still meet the three requirements above.

Finding the domain.

Here are some examples. Notice that the differential equation, its solution, and the initial condition all come into consideration.

2000 AB 6: After finding the solution 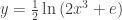$y=\frac{1}{2}\ln \left( 2{{x}^{3}}+e \right)$ , finding the domain is a pre-calculus question, requiring one to solve the simple inequality $2{{x}^{3}}+e>0$ . The domain is $\displaystyle x>\sqrt[3]{\frac{-e}{2}}$ .

2006 AB 5: Will be discussed below in answer to another question he asked.

2008 AB 5: The differential equation is undefined at x = 0 and the initial condition is to the right of this. So, the domain is all positive numbers.

2011 AB5/BC5: The domain is given in the stem; Time starts now and the differential equation applies “for the next 20 years”, so, 0 < x < 20

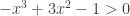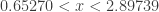2013 AB 6: The solution is $y=-\ln \left( -{{x}^{3}}+3{{x}^{2}}-1 \right)$ , So the domain is all x such that x = 1 (the initial condition) and for which $-{{x}^{3}}+3{{x}^{2}}-1>0$ . No further simplification was given. By graphing calculator the range is about $0.65270<x<2.89739$ .

2013 BC 5: The solution, 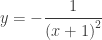$\displaystyle y=-\frac{1}{{{\left( x+1 \right)}^{2}}}$ , contains a vertical asymptote at x = –1. Since the initial condition is (0, –1) the domain is x > –1; the side of the asymptote containing the initial condition.

2014 AB 6: Neither the equation, nor the solution, 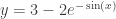$\displaystyle y=3-2{{e}^{-\sin \left( x \right)}}$ , has any values for which x is undefined; so, the domain is all real numbers.

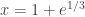2016 AB 4: The differential equation is $\displaystyle \frac{dy}{dx}=\frac{{{y}^{2}}}{x-1}$ with f(2) = 3. The solution $\displaystyle y=\frac{1}{\tfrac{1}{3}-\ln \left( x-1 \right)}$ , has a vertical asymptote where the denominator is 0, namely $x=1+{{e}^{1/3}}$ , and is undefined (because of the logarithm) for 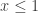$x\le 1$ . The largest open interval containing the initial condition is between these two values, namely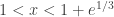 $1<x<1+{{e}^{1/3}}$

2017 AB 4: The endpoints of the domain are stated in the stem of the problem. The time t begins when the potato is removed from the oven so t > 0 and the differential equation in (c) is given for t < 10. So the domain is 0 < t < 10.

2018 AB 6: Both the differential equation and its general solution are defined for all Real numbers: 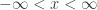$\displaystyle -\infty <x<\infty$

All of these require no “calculus”- they are “find the domain” questions from pre-calculus with the concern about vertical asymptotes. There are some other considerations. A longer and far more detailed discussion of this can be found in “The Domain of Solutions to Differential Equations”, by former chief reader Larry Riddle.

I think that answers the first question my reader asked. As to his second and third questions, I guess the answer is yes. At some point students will be asked to state the domain of a differential equation. My guess is it will be a fairly easy one-point part of a free-response question. If solving the differential equation is necessary, then it seems too long for a multiple-choice question. This is all guesswork on my part; I have no knowledge of what’s on future exams.

2019 AB 4: The solution is a polynomial and there valid for all Real numbers.

2021 AB 6: The solution contains a power of e. The domain is all Real numbers.

2021 BC 4: The solution contains terms with ln(x). The domain is all x > 0.

2022 AB 5: The domain is all Real Numbers

My reader also asked about absolute value

Another question that may be related to this topic is the relevancy of the absolute value signs in the solutions to differential equations. When can they be kept in the solution, and when are they redundant?

Absolute values can really confuse kids. See my posts “Absolutely” and “Absolute Value.” Pre-calculus topics, yes, but they come back again and again.

Here are two examples about absolute values and domains:

2005 AB 6: After separating the variables and applying the initial condition we arrive at ${{y}^{2}}=-2{{x}^{2}}+3$ . This is not a function; its graph is an ellipse. We cannot just write $y=\pm \sqrt{-2{{x}^{2}}+3}$ , since that is not a function either. With the initial condition f(1) = –1, we have $\sqrt{{{y}^{2}}}=\left| y \right|=-y$ . 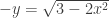Then choose the half of the ellipse where y is negative $-y=\sqrt{3-2{{x}^{2}}}$ and $y=-\sqrt{3-2{{x}^{2}}}$ . The domain is $-\sqrt{1.5}<x<\sqrt{1.5}$ .

2006 AB 5. The initial value question is to solve 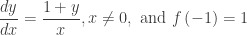$\displaystyle \frac{dy}{dx}=\frac{1+y}{x},x\ne 0,\text{ and }f\left( -1 \right)=1$ .

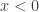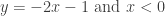
The domain was asked for. Since it is given that $x\ne 0$ , and there are no other “bad” places, the domain must be one side of the y-axis or the other. The initial condition tells us that the domain is to the left of the y-axis, $x<0$ . Since, this is so, $\left| x \right|=-x$ and the solution simplifies to $y=-2x-1\text{ and }x<0$

I really appreciate questions from readers, so if you want to ask about some topic please ask me at lnmcmullin@aol.com . I’m always looking for new topics to write about – or said a different way, I’m running out of ideas!

Revised 4-3-18

Revised 12-23-2018 to include the 2017 and 2018 differential equation questions.

Revised 11-23-2020 – 2019 exam

Revised 1-11-2021

Sequences and Series (Type 10 for BC only)

Posted on April 4, 2017 by Lin McMullin

Convergence tests for series appear on both sections of the BC Calculus exam. In the multiple-choice section, students may be asked to say if a sequence or series converges or which of several series converge.

The Ratio test is used most often to determine the radius of convergence and the other tests to determine the exact interval of convergence by checking the convergence at the end points. Click here for a Convergence test chart students should be familiar with; this list is also on the resource page.

On the free-response section there is usually one full question devoted to sequences and series. This question usually involves writing a Taylor or Maclaurin polynomial for a series.

Students should be familiar with and able to write several terms and the general term of a series. They may do this by finding the derivatives and constructing the coefficients from them, or they may produce the series by manipulating a known or given series. They may do this by substituting into a series, differentiating it or integrating it.

The general form of a Taylor series is $\displaystyle \sum\limits_{n=0}^{\infty }{\frac{{{f}^{\left( n \right)}}\left( a \right)}{n!}{{\left( x-a \right)}^{n}}}$ ; if a = 0, the series is called a Maclaurin series.

What Students Should be Able to Do

Use the various convergence tests to determine if a series converges. The test to be used is rarely given so students need to know when to use each of the common tests. For a summary of the tests click: Convergence test chart.
Write the terms of a Taylor or Maclaurin series by calculating the derivatives and constructing the coefficients of each term.
Distinguish between the Taylor series for a function and the function. Do NOT say that the Taylor polynomial is equal to the function (this will lose a point); say it is approximately equal.
Determine a specific coefficient without writing all the previous coefficients.
Write a series by substituting into a known series, by differentiating or integrating a known series, or by some other algebraic manipulation of a series.
Know (from memory) the Maclaurin series for sin(x), cos(x), e^x and $\displaystyle \tfrac{1}{1-x}$ and be able to find other series by substituting into them.
Find the radius and interval of convergence. This is usually done by using the Ratio test and checking the endpoints.
Be familiar with geometric series, its radius of convergence, and be able to find the number to which it converges, $\displaystyle {{S}_{\infty }}=\frac{{{a}_{1}}}{1-r}$ . Re-writing a rational expression as the sum of a geometric series and then writing the series has appeared on the exam.
Be familiar with the harmonic and alternating harmonic series. These are often useful series for comparison.
Use a few terms of a series to approximate the value of the function at a point in the interval of convergence.
Determine the error bound for a convergent series (Alternating Series Error Bound and Lagrange error bound). See my post of February 22, 2013.
Use the coefficients (the derivatives) to determine information about the function (e.g. extreme values).
Understand absolute and conditional convergence. If the series of the absolute values of the terms of a series converges, then the original series is said to absolutely convergent (or converges absolutely). If the series of absolute values diverges, then the original series may (or may not) converge; if it converges it is said to be conditionally convergent.

This list is quite long, but only a few of these items can be asked in any given year. The series question on the free-response section is usually quite straightforward. Topics and convergence test may appear on the multiple-choice section. As I have suggested before, look at and work as many past exam questions to get an idea of what is asked and the difficulty of the questions. Click on Power Series in the “Posts by Topic” list on the right side of the screen to see previous posts on Power Series.

The concludes the series of posts on the type questions in review for the AP Calculus exams.

Friday April 7, 2017 The Domain of the solution of a differential equation.

Polar Curves (Type 9 for BC only)

Posted on March 31, 2017 by Lin McMullin

Ideally, as with parametric and vector functions, polar curves should be introduced and covered thoroughly in a pre-calculus course. Questions on the BC exams have been concerned with calculus ideas related to polar curves. Students have not been asked to know the names of the various curves (rose, curves, limaçons, etc.). The graphs are usually given in the stem of the problem, but students should know how to graph polar curves on their calculator, and the simplest by hand.

What students should know how to do:

Calculate the coordinates of a point on the graph,
Find the intersection of two graphs (to use as limits of integration).
Find the area enclosed by a graph or graphs: Area = $\displaystyle A=\tfrac{1}{2}\int_{{{\theta }_{1}}}^{{{\theta }_{2}}}{(r(}$ θ $\displaystyle ){{)}^{2}}d$ θ
Use the formulas $x\left( \theta \right)\text{ }=~r\left( \theta \right)\text{cos}\left( \theta \right)~~\text{and}~y\left( \theta \right)\text{ }=~r(\theta )\text{sin}\left( \theta \right)~$ to convert from polar to parametric form,
Calculate $\displaystyle \frac{dy}{d\theta }$ and $\displaystyle \frac{dx}{d\theta }$ (Hint: use the product rule on the equations in the previous bullet).
Discuss the motion of a particle moving on the graph by discussing the meaning of $\displaystyle \frac{dr}{d\theta }$ (motion towards or away from the pole), $\displaystyle \frac{dy}{d\theta }$ (motion in the vertical direction) or $\displaystyle \frac{dx}{d\theta }$ (motion in the horizontal direction).
Find the slope at a point on the graph, $\displaystyle \frac{dy}{dx}=\frac{dy/d\theta }{dx/d\theta }$ .

This topic appears only occasionally on the free-response section of the exam instead of the Parametric/vector motion question. The most recent on the released exams were in 2007, 2013, 2014, and 2017. If the topic is not on the free-response then 1, or maybe 2 questions, probably finding area, can be expected on the multiple-choice section.

Shorter questions on these ideas appear in the multiple-choice sections. As always, look over as many questions of this kind from past exams as you can find.

Tuesday April 4: For BC Sequences and Series.

Friday April 7, 2017 The Domain of the solution of a differential equation.

Teaching Calculus

The pleasure lies not in discovering the truth, but in searching for it.

Author Archives: Lin McMullin

Who’d a thunk it?

Synthetic Summer Fun

Exams or Vacation?

NCTM Calculus Panel Notes

Domain of a Differential Equation

Sequences and Series (Type 10 for BC only)

Polar Curves (Type 9 for BC only)

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this: