Applications of Integration – Accumulation 1

Posted on December 18, 2018 by Lin McMullin

The idea that the definite integral is an “accumulator” means that integrating a rate of change over an integral gives the net amount of change over the interval.Many of the application of integration are based on this idea. Here are some past posts on this idea.

Accumulation An introductory activity to explore accumulation and the relationship between an accumulation and derivatives

Accumulation: Need an Amount? (1-21-2013) An important and always tested application.

AP Accumulation Questions (1-23-2013) Two good questions for teaching and learning accumulation.

Graphing with Accumulation 1 (1-25-2013) Everything you need to know about the graph of a function given its derivative can be found using integration techniques. Increasing and decreasing.

Graphing with Accumulation 2 (1-28-2013) Everything you need to know about the graph of a function given its derivative can be found using integration techniques. Concavity.

Next Tuesday is Christmas (already). There will be no post until Tuesday January 1, 2019 when I will there will be several more links to post on accumulation.

Happy Holidays, Merry Christmas, and Happy New Year.

Applications of Integration – Volume

Posted on December 11, 2018 by Lin McMullin

One of the major applications of integration is to find the volumes of various solid figures.

Volume of Solids with Regular Cross-sections This is where to start with volume problems. After all, solids of revolution are just a special case of solids with regular cross-sections.

Volumes of Revolution

Subtract the Hole from the Whole and Does Simplifying Make Things Simpler?

Visualizing Solid Figures

Visualizing Solid Figures 1 Making models et al.
Visualizing Solid Figures 2 Using Winplot to visualize solids with regular cross-sections.
Visualizing Solid Figures 3 Using Winplot to visualize the Disk and Washer methods.
Visu alizing Solid Figures 4 Using Winplot to visualize finding volumes by cylindrical shells. While no problem on the AP Calculus exams will require a solution by the Cylindrical Shell method, students may use the method and be eligible for full credit. So this is “enrichment.”
Challenge – the half-full problem comparing the disk and shell methods and Visualizing Solid Figures 5 the detailed solution

Why you Never Need Cylindrical Shells

Painting a Point

Revised and update October 22, 2018

Y the FTC?

Posted on December 7, 2018 by Lin McMullin

So, you’ve finally proven the Fundamental Theorem of Calculus and have written on the board:

$\displaystyle \int_{a}^{b}{{{f}'\left( x \right)dx=f\left( b \right)-f\left( a \right)}}$

And the students ask, “What good is that?” and “When are we ever going to use that?” Here’s your answer.

There are two very important uses of this theorem. Show them BOTH uses right away to help your students see why the FTC is so useful and important.

First, in words the theorem says that “the integral of a rate of change is the net amount of change.” So, if you are given a rate of change (as you are every year on the AP Calculus exam) and asked to find the amount of change (as you are every year on the AP Calculus exam), this is what you use, Show an example such as 2015 AB 1/BC1 that states,

“The rate at which rainwater flows into a drain pipe is modeled by the function R, where $R\left( t \right)=20\sin \left( {\frac{{{{t}^{2}}}}{{35}}} \right)$ cubic feet per hour….

“(a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval ?”

The answer is of course, $\displaystyle \int_{0}^{8}{{20\sin \left( {\frac{{{{t}^{2}}}}{{35}}} \right)dt}}$ . (Which they will soon learn how to evaluate.)

Second, a more immediate use is to avoid all that work you’ve been doing setting up Riemann sums and finding their limits. No more of that! Give them this integral to evaluate:

$\displaystyle \int_{2}^{7}{{2xdx}}$

Draw the trapezoid representing the area between the graph of 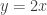$y=2x$ and the x-axis on the interval [2,7] and find its area =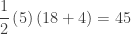 $\displaystyle \frac{1}{2}\left( 5 \right)\left( {18+4} \right)=45$

Then ask, “Does anyone know of a function whose derivative is 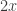$2x$ ?” Let them think for a minute and someone will say, “Yeah, it’s 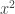${{x}^{2}}$ ” And then show them

$\displaystyle \int_{2}^{7}{{2xdx}}={{7}^{2}}-{{2}^{2}}=45$

Then go for a harder one: 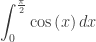$\displaystyle \int_{0}^{{\frac{\pi }{2}}}{{\cos \left( x \right)dx}}$

“Does anyone know a function whose derivative is $\cos \left( x \right)$ ?”

“Why yes, it’s $\sin \left( x \right)$ ”

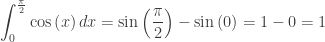
So, $\displaystyle \int_{0}^{{\frac{\pi }{2}}}{{\cos \left( x \right)dx}}=\sin \left( {\frac{\pi }{2}} \right)-\sin \left( 0 \right)=1-0=1$

That was easy!

If you want to challenge them and review some functions of the “special angles” try this one:

$\displaystyle \int_{{\frac{\pi }{6}}}^{{\frac{{4\pi }}{3}}}{{\cos \left( x \right)dx}}=\sin \left( {\frac{{4\pi }}{3}} \right)-\sin \left( {\frac{\pi }{6}} \right)=\frac{{\sqrt{3}}}{2}-\frac{1}{2}$

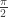Tie the two parts together: Look at the graph of $y=\sin \left( x \right)$ . How much does it change from 0 to $\frac{\pi }{2}$ ? How much does it change from $\frac{\pi }{6}$ to $\frac{{4\pi }}{3}$ ?

Sum up, by looking ahead:

“The function whose derivative is …” is called the antiderivative.
Using antiderivatives to evaluate definite integrals is easy; the hard part is finding the antiderivatives, since they are not all as straightforward as the two examples above. So, next we need to spend a few weeks learning how to find antiderivatives.[1]
Given a derivative, finding its antiderivative is also the start of solving differential equations. This, too, will soon be a concern in the course.

[1] As I’ve written before, this is where it seems logical place to teach antiderivatives. Now students have a reason to find them. Teaching antidifferentiation after differentiation, before integration, seems like an intellectual exercise. Sure, it’s fun, but now we have a need for it.

Applications of Integration – Area & Average Value

Posted on December 4, 2018 by Lin McMullin

Usually the first application of integration is to find the area bounded by a function and the x-axis, followed by finding the area between two functions. We begin with these problems

First some calculator hints

Graphing Integrals using a graphing calculator to graph functions defined by integrals

Graphing Calculator Use and Definition Integrals – Exam considerations Suggestions for using a calculator efficiently in area/volume problems

Area Problems

Area Between Curves

Under is a Long Way Down How to avoid “negative area.”

Density Functions Not often asked on the AP exams, but a good application related to area, nevertheless.

Who’d a thunk it? Some more complicated area problems for CAS solution.

Improper Integrals and Proper Areas – a BC topic

Average Value

Average Value of a Function

What’s a Mean Old Average Anyway – Discusses the different “average” in calculus

Half-full and Half Empty – Average Value

Average Value Activity to help students discover the Average Value formula

Revised and updated October 22, 2018

Teaching Calculus

The pleasure lies not in discovering the truth, but in searching for it.

Monthly Archives: December 2018

Applications of Integration – Accumulation 1

Applications of Integration – Volume

Y the FTC?

Applications of Integration – Area & Average Value

Share this:

Share this:

Share this:

Share this: