Introducing Power Series

Posted on January 30, 2018 by Lin McMullin

The posts for the next several weeks will be on topics tested only on the BC Calculus exams. Continuing with some posts on introducing power series (the Taylor and Maclaurin series)

: Brook Taylor (1685 – 1731)

: Colin Maclaurin (1698 – 1746)

Introducing Power Series 1 Two examples to lead off with.

Introducing Power Series 2 Looking at the graph of a power series foreshadows the idea of the interval of convergence.

Introducing Power Series 3 The Taylor Approximating Polynomial with examples of using a series to approximate.

Graphing Taylor Polynomials Graphing calculator hints.

Units

Posted on January 26, 2018 by Lin McMullin

I had a question from a reader recently asking about how to determine the units for derivatives and integrals.

Derivatives: The units of the derivative are the units of dy divided by the units of dx, or the units of the dependent variable (f(x) or y) divided by the units of the independent variable (x). The reason for this comes from the definition of the derivative:

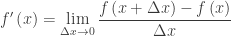
$\displaystyle {f}'\left( x \right)=\underset{{\Delta x\to 0}}{\mathop{{\lim }}}\,\frac{{f\left( {x+\Delta x} \right)-f\left( x \right)}}{{\Delta x}}$

In the quotient the numerator has the units of f and in the denominator the has the same units as x.

Definite Integrals: The units of a definite integral are the units of the integrand f(x) multiplied by the units of dx. This comes directly from the definition of a definite integral:

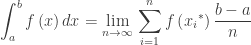
$\displaystyle \int_{a}^{b}{{f\left( x \right)dx}}=\underset{{n\to \infty }}{\mathop{{\lim }}}\,\sum\limits_{{i=1}}^{n}{{f\left( {{{x}_{i}}^{*}} \right)\frac{{b-a}}{n}}}$

The factor (b – a) has the same units a x, the independent variable, and the f(x) has whatever units it has. From the Riemann sum we can see that since these factors are multiplied, that product is the units of the definite integral.

The integrand is the derivative of its antiderivative (by the FTC) and so its units are often derivative units (miles per hour, furlongs per fortnight, etc.). When multiplied by (b – a)/n its units “cancel” the units of the denominator of f(x) and the result is the units of the numerator of f(x). This is not always the case*, therefore, multiplying the units is safest.

*The definite integral 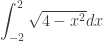$\displaystyle \int_{{-2}}^{2}{{\sqrt{{4-{{x}^{2}}}}dx}}$ gives the area of a semi-circle of radius 2 feet. The units of the radical are feet and represent the vertical distance from the x-axis to a point in the semi-circle; the dx is the horizontal side of the Riemann sum rectangles also in feet. Both are measured in the same linear units and the area is their product: feet times feet or square feet.

Infinite Series

Posted on January 23, 2018 by Lin McMullin

The posts for the next several weeks will be on topics tested only on the BC Calculus exams. The first few weeks will be past posts on sequences and series. That will be followed, in February, by a discussion of Parametric and Vector functions, and Polar equation.

We begin with series.

Comparison Test Chart A table summarizing the convergence test required for the AP Calculus BC exam, their hypotheses and Conclusions (Updated 2-1-18)

What Conversion Test Should I Use? Part 1

What Conversion Test Should I Use? Part 2

Good Question 14 A riff on the Integral Test

Everyday series decimals and roots

Amortization Calculating your mortgage payment – a practical and useful example of finite series

Revised 2-26-2018

Posts on Differential Equations – 2

Posted on January 16, 2018 by Lin McMullin

Posts on Differential Equations – 1

Posted on January 9, 2018 by Lin McMullin

Next in line are differential equations. Here are links to some past posts on differential equations

Differential Equations Outline of basic ideas for AB and BC calculus

Slope Fields

Euler’s Method – a BC only topic

Domain of a Differential Equation mentioned on the new Course and Exam Description

Good Question 6 2000 AB 4

Additional post on differential equations next week.

Applications of Integration, part 3: Accumulation

Posted on January 2, 2018 by Lin McMullin

Integration, at its basic level, is addition. A definite integral is a sum (a Riemann sum). When you add things you get an amount of whatever you are adding: you accumulate. Here are some previous posts on this important idea that often shows up on the AP Calculus exams (usually the first free-response question!)

Accumulation: Need an Amount?

Good Question 6 – 2000 AB 4 One of my favorite questions

Painting a Point

Real “Real Life” Graph Reading

Jobs, Jobs, Jobs are real life accumulation problem based on a graph

Graphing with Accumulation 1 Increasing and decreasing.

Graphing with Accumulation 2 Concavity

Accumulation and Differential Equations Differential equations will be considered next week, but this idea relates to integration.

Good Question 8 – or Not?

Rate and Accumulation Questions (Type 1)