Tag Archives: quotient rule

Why Techniques for Differentiation?

Posted on by
Reply

You have learned and used formulas for finding the derivatives of the Elementary Functions. These can be applied to functions made up of the Elementary Functions and extended to other expressions.

Many functions are made by combining the Elementary Functions. For example, polynomials are the sum and differences of a constants and powers of x multiplied by constants (their coefficients).

The functions you will look at next are the sums, differences, products, quotients, and/or composites of the Elementary Function. You will learn five techniques for handling these.

Sums and differences are found by differentiating the individual terms. Then there are the Product Rule for products of functions, the Quotient Rule for quotients and the Chain Rule for compositions. The techniques are often used in combinations.

Learn to see the patterns in the functions and learn what procedure to use for each.

HINT: Memorize the techniques as you learn them. After all these years, I still say the formulas and techniques as I use them. So, for products I repeat in my mind “the first times the derivative of the second plus the second times the derivative of the first” as I do the computation. Forget about mnemonics – just say the technique as you use it, and you’ll memorize it easily. 

Implicit relations and inverses have their own techniques; they use the basic formulas and techniques in different ways.

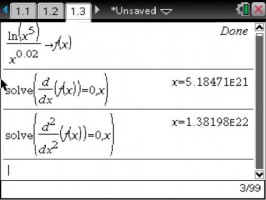
Since derivatives are functions, they have their own derivatives. The derivative of the first derivative is called the second derivative. Then there is the third derivative, the fourth derivative and so on. Mostly, you will use only the first three. No new rules to learn; higher order derivatives are computed the same way as the first derivative, and in fact, they often get simpler.

The proofs of the formulas and techniques (they are really theorems) are interesting from a mathematical point of view. You should follow along when your teacher shows them to you so that you understand why they work and where they come from. You will not be asked to reproduce the proofs on the AP Calculus Exam.

AP Calculus Course and Exam Description Unit 3 Sections 2.8 – 2.10 and Unit 3 all

Differentiation Techniques

Posted on by
Reply

Maria Gaetana Agnesi

So, no one wants to do complicated limits to find derivatives. There are easier ways of course. There are a number of quick ways (rules, formulas) for finding derivatives of the Elementary Functions and their compositions. Here are some ways to introduce these rules; these are the subject of this week’s review of past posts.

Why Radians?

The Derivative I        Guessing the derivatives from the definition

The Derivative II      Using difference Quotient to graph and guess

The Derivative Rules I    The Power Rule

The Derivative Rules II       Another approach to the Product Rule from my friend Paul Foerster

The Derivative Rules III     The Quotient Rule developed using the Power Rule, an approach first suggested  by Maria Gaetana Agnesi (1718 – 1799) who was helping her brother learn the calculus.

Next week: The Chain Rule.

 

 

 

 

Far Out!

Posted on by
1

A monster problem for Halloween.

A while ago I suggested you look at \displaystyle \underset{x\to \infty }{\mathop{\lim }}\,\frac{\ln \left( {{x}^{5}} \right)}{{{x}^{0.02}}} , which using the dominance idea is zero. Of course your students may try graphing or a table. Here’s the graph done by a TI-Nspire CAS. Note the scales.

This is not the way to go. Since the function is increasing near the origin, but the limit at infinity is zero there must be a maximum point where the function starts decreasing. And as the expression can never be negative once x > 1, there must be a point of inflection where the graph becomes concave up and can thereafter approach the x-axis from above as a horizontal asymptote. The maximum can be found by hand which makes for some great algebra manipulation practice:

\displaystyle \frac{d}{dx}\left( \frac{\ln \left( {{x}^{5}} \right)}{{{x}^{0.02}}} \right)=\frac{{{x}^{0.02}}\tfrac{5{{x}^{4}}}{{{x}^{5}}}-\ln \left( {{x}^{5}} \right)\left( 0.02{{x}^{-0.98}} \right)}{{{x}^{0.04}}}

\displaystyle \frac{d}{dx}\left( \frac{\ln \left( {{x}^{5}} \right)}{{{x}^{0.02}}} \right)=\frac{{{x}^{-0.98}}\left( 5-\left( 0.10 \right)\ln \left( x \right) \right)}{{{x}^{0.04}}}=\frac{50-\ln \left( x \right)}{10{{x}^{1.02}}}

Setting this equal to zero and solving gives x={{e}^{50}}\approx 5.185\times {{10}^{21}}

The second derivative is \displaystyle \frac{{{d}^{2}}}{d{{x}^{2}}}\left( \frac{\ln \left( {{x}^{5}} \right)}{{{x}^{0.02}}} \right)=\frac{-510+10.2\ln \left( x \right)}{100{{x}^{2.02}}}

and is zero when x = \displaystyle {{e}^{\frac{520}{10.2}}}\approx 1.382\times {{10}^{22}}

Okay, I skipped a few steps here, but you can challenge your students with that. Since we’re really interested in the solution here more than the solving ,this is really a good place to use a CAS calculator.

The first line in the figure above defines the function to save typing it each time. The second line finds the x-coordinate of the maximum point (how do we know this is a maximum?) and the third finds the x-coordinate of the point of inflection.  Much simpler this way!

Take a minute to consider the numbers. They are BIG! In fact, if the units on our graph paper are centimeters, then the maximum point is a little over 5,480 light-years away from the origin! The point of inflection is about 2.665 times farther at more than 14,607 light-years away!

Meanwhile the maximum value is only 91.9699 cm. That’s right centimeters, less than a meter. And the y-coordinate of the point of inflection is about 91.9524 cm. A drop of 0.0175 cm. in a horizontal distance of a little over 9,127 light-years.

Some problems are a lot less scary if done with technology.

Derivative Rules III

Posted on by
1

The Quotient Rule

This approach to the quotient rule is credited to Maria Gaetana Agnesi (1718 – 1799) who wrote the first known mathematics textbook Analytical Institutions (1748) to help her brothers learn algebra.

The quotient rule can also be proven from the definition of derivative. But here is a simpler approach – as a corollary of the product rule.

Begin by letting \displaystyle h\left( x \right)=\frac{f\left( x \right)}{g\left( x \right)}.

Then

f\left( x \right)=h\left( x \right)g\left( x \right) and {f}'\left( x \right)=g\left( x \right){h}'\left( x \right)+h\left( x \right){g}'\left( x \right).

Then solving for {h}'\left( x \right):

\displaystyle {h}'\left( x \right)=\frac{{f}'\left( x \right)-h\left( x \right){g}'\left( x \right)}{g\left( x \right)}

\displaystyle =\frac{{f}'\left( x \right)-\frac{f\left( x \right)}{g\left( x \right)}{g}'\left( x \right)}{g\left( x \right)}

\displaystyle =\frac{g\left( x \right){f}'\left( x \right)-f\left( x \right){g}'\left( x \right)}{{{\left( g\left( x \right) \right)}^{2}}}

Mnemonics

I’m not really one for mnemonics. I cannot spell SOHCOHTOA without saying to myself, “sine, opposite over hypotenuse; cosine, adjacent …” It seems better to me anyway to have student just memorize the formulas in words using the correct terms:

The derivative of a product is the first factor times the derivative of the second plus the second factor times the derivative of the first.

The derivative of a quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator all divided by the square of the denominator.

But whatever works for you. Lo Di Hi