Author Archives: Lin McMullin

The 2019 CED and This Blog

Posted on by
Reply

The new 2019 AP Calculus AB and BC Course and Exam Description is now available. New and experienced AP Calculus teachers should download a copy and read it carefully. (A paper copy with binder can be ordered here – it’s FREE.)

The main sections of the book are here with notes on each.

Part 1: General information about the program

  • About AP
  • AP Resources including a preview of the online AP Classroom opening on August 1, 2019
  • Prerequisites (p. 7)
    • 4 years of math high school before AP
    • Study of Elementary functions, and the language and properties of function in general
    • Students who take AP Calculus BC should have basic familiarity with sequences and series, as well as some exposure to parametric and polar equations. This is new and indicates that students should not be seeing sequences, series, parametric equation, vector equation, and polar equation for the first time in their BC course.

Part 2: The course framework

  • The revised Mathematical Practices. The practices have been reorganized into 4 categories with detail under each (p. 14).While written with the calculus in mind, these really apply to all mathematics courses. They make a good topic for several of your department or Math Vertical team meetings. Make a copy for your students and your colleagues.
    • Implementing Mathematical Processes
    • Connecting Representations
    • Justification
    • Communication and Notation
  • The course content.
      • The big ideas have been reorganized into three ideas.
        • Change
        • Limits
        • Analysis of Functions
      • In addition to the organization of the course content into 10 units there is information about how much of the exams test each unit, how to spiral the big ideas.
      • The online AP Classroom available on August 1, 2019 will include “Personal Progress Checks” with which each student can determine how well he or she has mastered the units.
      • Unit Guides: These guides serve almost as the lesson plans for the year and will certainly help in preparing your syllabus. This is the longest section.
          • Each of the 10 units breaks the required course content giving the Enduring Understandings (EU), Learning Objectives (LO), and Essential Knowledge (EK) for each topic.
          • There are 6 – 15 topics in each unit.
          • Each unit begins with a paragraph on Developing Understanding, Building the Mathematical Practices, and Preparing for the AP Exam.
          • Sample instruction activates list activities for instruction for each topic in the unit.
          • In the sidebars are link to other resources.

Part 3: Instructional Approaches

  • Notes on textbooks, calculators, and professional organizations.
  • Instructional strategies – an outline of dozens of strategies you can use in your class. Each is defined and explained briefly.
  • Developing the Mathematical Practices – this section identifies skills, sample key questions, activities and instructional strategies for each
  • Exam Overview – gives information on the exams, how topics are weighted, how each unit is weighted, how the learning is assessed etc.
  • A list of “task verbs” given the meaning of the task students are asked to do on the free-response questions. This should be very helpful. Make a copy for your students. (p. 227)
  • Sample multiple-choice and free response questions with answers. Each is indexed to unit and LO to give you an idea of how each LO can be tested.

I have written a correlation between the topics in each unit and my blog posts. This can be found under the “Topics” tab in the menu bar at the top of the page (see figure below). The blog posts, written over the past 7 years, do not align perfectly with the topics and units. There are some posts that apply to several topics and some topics with (alas) no posts. I will update these with new posts from time to time and add any posts I’ve overlooked. I hope this will help you find your way around.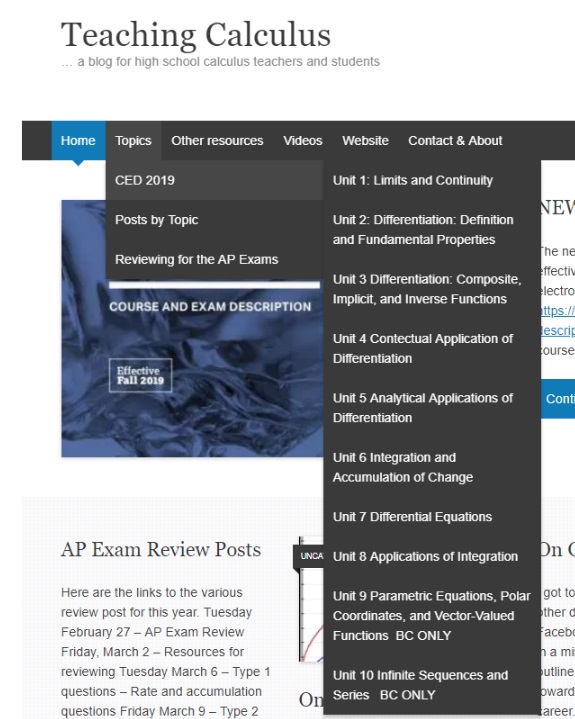

As always, I appreciate any feedback, suggestions, corrections etc.

 

 

 

 

 

 

 

NEW AP Calculus CED Is Now Available

Posted on by
Reply

The new Course and Exam Description for AP Calculus AB & BC (CED 2019) effective for the  coming school year has been published and is available electronically at the course homepages. The direct link is

https://apcentral.collegeboard.org/pdf/ap-calculus-ab-bc-course-and-exam-description-0.pdf?course=ap-calculus-ab

This document is for both AB and BC courses.

There will be no change in the exam style and format, and no change in what is tested on the exams.

The organization has changed from the 2016 CED. Instead of a list of topics the course is organized into 10 Units with the topics for each unit. It is almost the start of a syllabus for the course. (No one is required to follow the outline. You may do your own thing, so long as you teach the required content.)  The electronic version contains live links to other resources and addition material to help you organize and teach your course.

The CED 2019 is also available free, gratis, for nothing in a binder so you can intersperse your own notes, worksheet, and activities in each unit. AP teachers in the United States who have completed the AP Course Audit can request a free copy of the binder by January 31, 2020. The binders will be mailed beginning in June 2019. Sign up to get yours here.

Looking ahead – August: the AP Classroom.

On August 1, 2019 the new AP Classroom will open online. This includes thousands of actual AP exam questions from past exams, AP files, and 1200 new questions. They are organized by the Units in the CED-2019. Teachers may access them and allow their students to do so by assigning them electronically. Feedback for students will include not just the correct answers but a discussion of the mistakes that may lead to the wrong answers of the multiple-choice questions. For more information and the other features of the AP Classroom use the links above to go to the course homepage and scroll down. You may also like this short video. It has more information about the AP Classroom.

Other AP Courses.

A new CED and the AP Classroom material is available for all AP 35 Courses (except AP Computer Science Principles, AP Seminar, and AP Research). Please be sure teachers of other AP Courses in your school and district are aware of this.

 

 

 

 

 

 

Tuesday and Beyond

Posted on by
Reply

So, Tuesday is the day. My usual suggestion for Monday is to get the kids both relaxed and psyched. They know it by now; not much more you can pour into their heads. So, not last minute advice or hints.

Good Luck and best wishes.

Looking ahead – May: the new Course and Exam Description for 2019

The College Board has some very major and important things coming up.

Next week, May 20 or thereabout, the new Course and Exam Description, CED-2019, will be published. It will be available electronically at the course homepages. Look for it here: Homepage for AB and homepage for BC.- the document is the same on both pages:

There will be no change in the exam style and format, and no change in what is tested on the exams.

The organization has changed from the 2016 CED. Instead of a list of topics the course is organized into 10 Units with the topics for each unit. It is almost the start of a syllabus for the course. (No one is required to follow the outline. You may do your own thing, so long as you teach the required content.)  The electronic version contains live links to other resources and addition material to help you organize and teach your course.

The CED-2019 is also available free, gratis, for nothing in a binder so you can intersperse your own notes, worksheet, and activities in each unit. AP teachers in the United States who have completed the AP Course Audit can request a free copy of the binder by January 31, 2020. The binders will be mailed beginning in June 2019. Sign up to get yours here.

Looking ahead – August: the AP Classroom.

On August 1, 2019 the new AP Classroom will open online. This includes thousands of actual AP exam questions from past exams, AP files, and 1200 new questions. They are organized by the Units in the CED-2019. Teachers may access them and allow their students to do so by assigning them electronically. Feedback for students will include not just the correct answers but a discussion of the mistakes that may lead to the wrong answers of the multiple-choice questions. For more information and the other features of the AP Classroom use the links above to go to the course homepage and scroll down. You may also like this short video. It has more information about the AP Classroom.

Other AP Courses.

A new CED and the AP Classroom material will be available for all AP 35 Courses (except AP Computer Science Principles, AP Seminar, and AP Research) on the same dates as above. Please be sure teachers of other AP Courses in your school and district are aware of this.

 

 

 

 

 

 

AP Exam Review Posts

Posted on by
Reply

Here are the links to the various review posts for this year.

Type 10: Sequences and Series Questions

Posted on by
Reply

The last BC question on the exams usually concerns sequences and series. The question usually asks students to write a Taylor or Maclaurin series and to answer questions about it and its interval of convergence, or about a related series found by differentiating or integrating. The topics may appear in other free-response questions and in multiple-choice questions. Questions about the convergence of sequences may appear as multiple-choice questions. With about 8 multiple-choice questions and a full free-response question this is one of the largest topics on the BC exams.

Convergence tests for series appear on both sections of the BC Calculus exam. In the multiple-choice section, students may be asked to say if a sequence or series converges or which of several series converge.

The Ratio test is used most often to determine the radius of convergence and the other tests to determine the exact interval of convergence by checking the convergence at the end points. Click here for a convergence test chart students should be familiar with; this list is also on the resource page.

Students should be familiar with and able to write several terms and the general term of a Taylor or Maclaurin series. They may do this by finding the derivatives and constructing the coefficients from them, or they may produce the series by manipulating a known or given series. They may do this by substituting into a series, differentiating it or integrating it.

The general form of a Taylor series is \displaystyle \sum\limits_{n=0}^{\infty }{\frac{{{f}^{\left( n \right)}}\left( a \right)}{n!}{{\left( x-a \right)}^{n}}}; if a = 0, the series is called a Maclaurin series.

What Students Should be Able to Do 

  • Use the various convergence tests to determine if a series converges. The test to be used is rarely given so students need to know when to use each of the common tests. For a summary of the tests click: Convergence test chart.  and the posts “What Convergence Test Should I use?” Part 1 and Part 2
  • Understand absolute and conditional convergence. If the series of the absolute values of the terms of a series converges, then the original series is said to absolutely convergent (or converges absolutely). If the series of absolute values diverges, then the original series may or may not converge; if it converges it is said to be conditionally convergent.
  • Write the terms of a Taylor or Maclaurin series by calculating the derivatives and constructing the coefficients of each term.
  • Distinguish between the Taylor series for a function and the function. DO NOT say that the Taylor polynomial is equal to the function (this will lose a point); say it is approximately equal.
  • Determine a specific coefficient without writing all the previous coefficients.
  • Write a series by substituting into a known series, by differentiating or integrating a known series, or by some other algebraic manipulation of a series.
  • Know (from memory) the Maclaurin series for sin(x), cos(x), ex and \displaystyle \tfrac{1}{1-x} and be able to find other series by substituting into them.
  • Find the radius and interval of convergence. This is usually done by using the Ratio test and checking the endpoints.
  • Be familiar with geometric series, its radius of convergence, and be able to find the number to which it converges, \displaystyle {{S}_{\infty }}=\frac{{{a}_{1}}}{1-r}. Re-writing a rational expression as the sum of a geometric series and then writing the series has appeared on the exam.
  • Be familiar with the harmonic and alternating harmonic series. These are often useful series for comparison.
  • Use a few terms of a series to approximate the value of the function at a point in the interval of convergence.
  • Determine the error bound for a convergent series (Alternating Series Error Bound and Lagrange error bound). See my posts on Error Bounds and the Lagrange Highway
  • Use the coefficients (the derivatives) to determine information about the function (e.g. extreme values).

This list is quite long, but only a few of these items can be asked in any given year. The series question on the free-response section is usually quite straightforward. Topics and convergence test may appear on the multiple-choice section. As I have suggested before, look at and work as many past exam questions to get an idea of what is asked and the difficulty of the questions. Click on Power Series in the “Posts by Topic” list on the right side of the screen to see previous posts on Power Series or any other topic you are interested in.

Free-response questions:

  • 2004 BC 6 (An alternate approach, not tried by anyone, is to start with \displaystyle \sin \left( {5x+\tfrac{\pi }{4}} \right)=\sin (5x)\cos \left( {\tfrac{\pi }{4}} \right)+\cos (5x)\sin \left( {\tfrac{\pi }{4}} \right))
  • 2016 BC 6
  • 2017 BC 6

Multiple-choice questions from non-secure exams:

  • 2008 BC 4, 12, 16, 20, 23, 79, 82, 84
  • 2012 BC 5, 9, 13, 17, 22, 27, 79, 90,

The concludes the series of posts on the type questions in review for the AP Calculus exams.

 

 

 

 

Type 9: Polar Equation Questions

Posted on by
Reply

Ideally, as with parametric and vector functions, polar curves should be introduced and covered thoroughly in a pre-calculus course. Questions on the BC exams have been concerned with calculus ideas related to polar curves. Students have not been asked to know the names of the various curves (rose curves, limaçons, etc.). The graphs are usually given in the stem of the problem, but students should know how to graph polar curves on their calculator, and the simplest by hand. Intersection(s) of two graph may be given or easy to find.

What students should know how to do:

  • Calculate the coordinates of a point on the graph,
  • Find the intersection of two graphs (to use as limits of integration).
  • Find the area enclosed by a graph or graphs: Area =\displaystyle A=\tfrac{1}{2}\int_{{{\theta }_{1}}}^{{{\theta }_{2}}}{(r(}θ\displaystyle ){{)}^{2}}dθ
  • Use the formulas x\left( \theta  \right)\text{ }=~r\left( \theta  \right)\text{cos}\left( \theta  \right)~~\text{and}~y\left( \theta  \right)\text{ }=~r(\theta )\text{sin}\left( \theta  \right)~  to convert from polar to parametric form,
  • Calculate \displaystyle \frac{dy}{d\theta } and \displaystyle \frac{dx}{d\theta } (Hint: use the product rule on the equations in the previous bullet).
  • Discuss the motion of a particle moving on the graph by discussing the meaning of \displaystyle \frac{dr}{d\theta } (motion towards or away from the pole), \displaystyle \frac{dy}{d\theta } (motion in the vertical direction), and/or \displaystyle \frac{dx}{d\theta } (motion in the horizontal direction).
  • Find the slope at a point on the graph, \displaystyle \frac{dy}{dx}=\frac{dy/d\theta }{dx/d\theta }.

When this topic appears on the free-response section of the exam there is no Parametric/vector motion question and vice versa. When not on the free-response section there are one or more multiple-choice questions on polar equations.

Free-response questions:

  • 2013 BC 2
  • 2014 BC 2
  • 2017 BC 2

Multiple-choice questions from non-secure exams:

  • 2008 BC 26
  • 2012 BC 26, 91

 

 

 

 

 

Type 8: Parametric and Vector Questions

Posted on by
1

The parametric/vector equation questions only concern motion in a plane.

In the plane, the position of a moving object as a function of time, t, can be specified by a pair of parametric equations x=x\left( t \right)\text{ and }y=y\left( t \right) or the equivalent vector \left\langle x\left( t \right),y\left( t \right) \right\rangle . The path is the curve traced by the parametric equations or the tips of the position vector. .

The velocity of the movement in the x- and y-direction is given by the vector \left\langle {x}'\left( t \right),{y}'\left( t \right) \right\rangle . The vector sum of the components gives the direction of motion. Attached to the tip of the position vector this vector is tangent to the path pointing in the direction of motion.

The length of this vector is the speed of the moving object. \text{Speed }=\sqrt{{{\left( {x}'\left( t \right) \right)}^{2}}+{{\left( {y}'\left( t \right) \right)}^{2}}}. (Notice that this is the same as the speed of a particle moving on the number line with one less parameter: On the number line \text{Speed}=\left| v \right|=\sqrt{{{\left( {x}'\left( t \right) \right)}^{2}}}.)

The acceleration is given by the vector \left\langle {{x}'}'\left( t \right),{{y}'}'\left( t \right) \right\rangle .

What students should know how to do:

  • Vectors may be written using parentheses, ( ), or pointed brackets, \left\langle {} \right\rangle , or even \vec{i},\vec{j} form. The pointed brackets seem to be the most popular right now, but all common notations are allowed and will be recognized by readers.
  • Find the speed at time t: \text{Speed }=\sqrt{{{\left( {x}'\left( t \right) \right)}^{2}}+{{\left( {y}'\left( t \right) \right)}^{2}}}
  • Use the definite integral for arc length to find the distance traveled \displaystyle \int_{a}^{b}{\sqrt{{{\left( {x}'\left( t \right) \right)}^{2}}+{{\left( {y}'\left( t \right) \right)}^{2}}}}dt. Notice that this is the integral of the speed (rate times time = distance).
  • The slope of the path is \displaystyle \frac{dy}{dx}=\frac{{y}'\left( t \right)}{{x}'\left( t \right)}. See this post for more on finding the first and second derivatives with respect to x.
  • Determine when the particle is moving left or right,
  • Determine when the particle is moving up or down,
  • Find the extreme position (farthest left, right, up, down, or distance from the origin).
  • Given the position find the velocity by differentiating; given the velocity find the acceleration by differentiating.
  • Given the acceleration and the velocity at some point find the velocity by integrating; given the velocity and the position at some point find the position by integrating. These are just initial value differential equation problems (IVP).
  • Dot product and cross product are not tested on the BC exam, nor are other aspects.

When this topic appears on the free-response section of the exam there is no polar equation question and vice versa. When not on the free-response section there are one or more multiple-choice questions on parametric equations.

Free-response questions:

  • 2012 BC 2
  • 2016 BC 2

Multiple-choice questions from non-secure exams

  • 2003 BC 4, 7, 17, 84
  • 2008 BC 1, 5, 28
  • 2012 BC 2