Monthly Archives: June 2021

Adapting 2021 AB 2

Posted on by
Reply

Two of nine. Continuing the series started in my last post, this post looks at the AB Calculus 2021 exam question AB 2. The series looks at each question with the aim of showing ways to use the question in with your class as is or by adapting and expanding it.  Like most of the AP Exam questions there is a lot more you can ask from the stem and a lot of other calculus you can discuss.

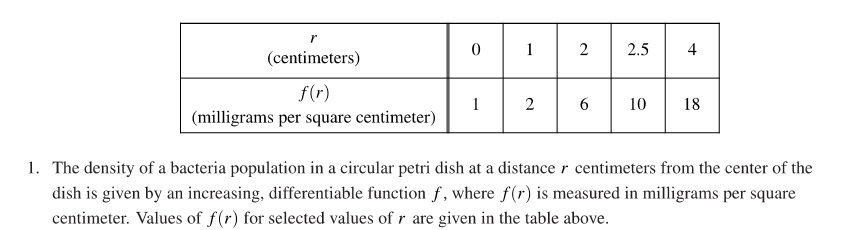
2021 AB 2

This is a Linear Motion Problem (Type 2) and has topics from Unit 4 of the current Course and Exam Description. Two particles are moving on the x-axis and the questions ask about their motion individually and relative to each other. The velocity and initial position are given for each particle. Parts (a), (c), and (d) are typical; (b) is the core of the problem.

The stem is:

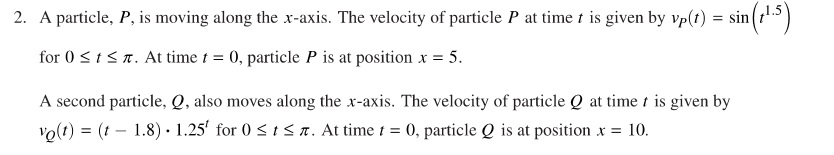
Part (a): Students are asked to find the position of each particle at time t = 1.

Discussion and ideas for adapting this question:

  • The expected approach is to calculate for each particle the initial position plus the displacement from t = 0 to t = 1. So, for P the computation is  P\left( 1 \right)=5+\int_{0}^{1}{{\sin \left( {{{t}^{{1.5}}}} \right)}}dt and similarly for Q(1). This is a calculator allowed question and students should use their calculator to find the answer and not do it by hand.
  • A different approach is to work it as an initial value differential equation problem. This will work but takes longer than the approach suggested above.
  • In class, it is worth discussing both methods.
  • You can adapt this by using a different time.
  • Another question is to find (only) the displacement if each particle over some time interval. Displacement has been asked in other years.
  • Ask “Will the particles ever collide? If so when and justify your answer. (Answer: no)

Part (b): Students were asked to determine if the particles are moving apart or towards each other at time t = 1. This is the main question and requires a careful analysis of their motion.

Discussion and ideas for adapting this question:

  • To determine this, students need to consider the velocity of the particles and their position (from part (a)). P is to the left of Q and moving right. Q is to the right of P and moving left, therefore, the distance between them is decreasing.
  • You can practice this analysis by using different times.
  • Ask students to carefully describe the motion of one or both particles: when it is moving left and right, when it changes direction, find the local maximum and minimum positions, etc. Notice that this is really the same as analyzing the shape of a graph. The connection between the two problems will help students understand both better. See: Motion Problems: Same Thing, Different Context

Part (c): A question about speed.

Discussion and ideas for adapting this question:

  • A typical question. Students should compare the signs of the velocity and acceleration of the particle. If they are the same, the speed is increasing; if different, decreasing.
  • You may ask this of the other particle.
  • You may ask this at different times.
  • See previous posts on speed here and here.

Part (d): Students were required to find the total distanced traveled by Q on the interval [0, π].

Discussion and ideas for adapting this question:

  • Since speed is the absolute value of the velocity, integrate the absolute value of the velocity. Do this on a calculator.
  • Adapt this by using a different interval.
  • Adapt this by using the other particle.
  • Another (longer) way to approach this question is to find where the particle changes direction by finding where the velocity changes from negative to positive and/or vice versa (i.e., the local extreme values). Then find the distanced traveled on each part of the “trip,” and add or subtract. This will reinforce a lot of the concepts involved in linear motion; that is why it is worth doing. As for the exam, integrating the absolute value is the way to go. However, if this were a non-calculator question, then it would have to be done this way. Find a simpler velocity and try it both ways.
  • To integrate the absolute value by hand, it is necessary to break the interval into subintervals depending on where the velocity is positive or negative. This is the same as the approach in the bullet immediately above. This, too, is worth showing to reinforce the definition of absolute value.

2021 revised as an in-out question.

There was some unhappiness over the fact that the 2021 AB Calculus exam did not have an in-out questions (Rate and Accumulation Type 1). However, this question does have two rates going in opposite directions. So, just to be ornery, I rewrote it as an in-out questions by changing the context and units while keeping the same velocity functions. The point is that the situation tested can be reframed in other ways. Seeing the same thing in different dress may help students concentrate on the calculus involved. Here it is:

A factory processes cement at the rate of  \displaystyle {{v}_{p}}\left( t \right)=\sin \left( {{{t}^{{1.5}}}} \right) tons per hour for \displaystyle 0\le t\le \pi hours. At time t = 0 the amount on hand is P = 5 tons.

The factory ships the cement at a rate given by  \displaystyle {{v}_{Q}}\left( t \right)=\left( {t-1.8} \right){{1.25}^{t}} tons per hour for \displaystyle 0\le t\le \pi hours. At time t = 0 the amount shipped is 10 tons.

  1. Find the amount processed and the amount shipped after hour.
  2. Is the amount on hand increasing or decreasing at time t = 1? Explain your reasoning.
  3. At what rate is the rate at which the cement is being shipped changing at t = 1? Is the amount being shipped increasing or decreasing at t = 1? Explain your reasoning.
  4. Find the total amount of cement processed over the time interval \displaystyle 0\le t\le \pi .

Next week 2021 AB 3/ BC 3.

I would be happy to hear your ideas for other ways to use this questions. Please use the reply box below to share your ideas.

Adapting 2021 AB 1 / BC 1

Posted on by
1

First of nine. One of the things many successful AP Calculus teachers do is to use past AP exam questions throughout the year. Individual multiple-choice exam questions are used as the topics they test are taught; free-response questions are adapted and expanded. There are several ways to do this:

  • Assign parts of a free-response (FR) question as is as the topic it tests is taught. Later, other parts from the same stem can be assigned. Including previously assigned parts is a spiraling technique. Once students see that you are doing this, they will be more likely to keep up to date on past topics.
  • Adapting and expanding the questions is another way to use FR questions.

This summer I will be discussing how to do just that. Each week I will look at one of the released 2021 FR questions and suggest how to expand and adapt it. Each stem allows for many more questions than can be asked on any one exam. You have the luxury of asking other things based on the same stem.

This summer’s series of posts will take one question at a time discuss it and suggest additional questions or explorations that may be asked. I will not be presenting solutions. They are available on AP Community bulletin board here and here. I will link the posts to the scoring standards when they are published.

2021 AB 1 / BC 1

This is a Reimann sum and Table question (Type 5) and covers topics from Units 6 and 8 from the current Course and Exam Description. All four parts are fairly typical for this type of problem. There is a little twist in part (b). The context is the density of bacteria growing in a petri dish.

Density is not listed in the Course and Exam Description. It is not covered well in many textbooks. Since it is not listed you need not teach it; exam questions referencing density have enough included information so that a student who has never seen the concept will still be able to answer the question. Keep this in mind as you look at each part; help your students see past the context and look at the calculus. More information on density see these posts Density Functions, and Good Question 15 and Good Question 16.

The stem for 2021 AB 1 / BC 1 reads:

Part (a): Students were asked to estimate the value of the derivative of f at r = 2.25 and explain its meaning, including units, in the context of the problem.  The expected procedure is to find the slope between the two values closest to r =2.25. The interpretation is the increase in density as you move away from the center. The units are milligrams per square centimeter per centimeter distant from the center \frac{{mg/c{{m}^{2}}}}{{cm}}.

Discussion and ideas for adapting this question:

  • AP exams have always asked this question at a value exactly half-way between two values in the table. You may change this to some other place such as r = 3 or r = 0.8.
  • Units of the derivative are always the units of the function divided by the units of the independent variable. Be sure your students understand this.
  • The units can be correctly written as  \frac{{mg}}{{c{{m}^{3}}}}, but here is a good change to discuss what the units mean. Why does “milligrams per square centimeter per centimeter distant from the center” make more sense?
  • Ask “Is there a point in the interval [2, 2.5] where the slope of the tangent line is 8? Justify your answer.” This makes use of the Mean Value Theorem.

Part (b) : As usual in this type of problem, students are asked to write a Riemann sum based on the intervals in the table. The difference here is that the integral being approximated, \displaystyle 2\pi \int_{0}^{4}{{rf\left( r \right)}}dr, has an “extra” factor of r in it.

Discussion and ideas for adapting this question:

  • The question asked for a right Riemann sum. You can easily adapt this by asking for a left Riemann sum, a midpoint Riemann sum, and/or a Trapezoidal approximation.
  • You may ask for a Riemann sum without the “extra” factor.
  • You may find a different Riemann sum problem and include an “extra” factor in it.
  • The integral is the integral for a radial density function. See the Density blog post cited above, example 2.
  • The radial density function looks like the integral for finding volumes by the method of cylindrical shells. This is more than a coincidence. Why?

Part (c): This part asked if the answer in (b) is an overestimate or an underestimate, with an explanation. For any approximation, some idea of its accuracy is important. In BC questions on power series approximations, a numerical estimate of the error bound is a common question.

Discussion and ideas for adapting this question:

  • Ask the same question for a different Riemann sum (left, midpoint, trapezoid).
  • The error in right and left Riemann sums estimates depend on whether the function is increasing or decreasing, and therefore on the first derivative. Midpoint and Trapezoidal approximation estimates are related to the concavity and therefore to the second derivative. See: Good Question 4)
  • A visual idea helps keep all this straight. Draw sketches showing the Riemann sum rectangles or trapezoids. Whether they lie above or below the graph of the function determines whether the approximation is an overestimate or underestimate.

Part (d): Typical of the Riemann sum table question is the final part with a related question based on a function and not based on the table.

Discussion and ideas for adapting this question:

  • This is a calculator allowed question. Students should not try to do the integration by hand.
  • The question asked for the average value of the function on an interval. Other questions you could ask are find the rate of change (derivative) at a point, the total mass \int_{1}^{4}{{rf\left( r \right)}}dr (note “extra” r), the average rate of change on an interval, etc.

Next week 2021 AB 2.

I would be happy to hear your ideas for other ways to use these questions. Please use the reply box below to share your ideas.

Summer … At last!

Posted on by
Reply

Summer … At last!

I hope you have all either completed your year or are close to it. Take some time to relax.

I am working on a series of nine summer post which will be begin on Tuesdays starting June 22. Each will look at one of the nine 2021 free-response questions. I will not be presenting their solutions; you can find them online. Rather, I will try to suggest ways that you can adapt the questions for use during the year. This may include ways to slightly change the question, ask additional questions from the same stem, and use the question to explore the topic further and deeper. I hope you’ll find them useful.

Please join me then and enjoy your summer!