Continuing my occasional series on Good Questions, today’s Good Question is a multiple-choice question from the 2008 AB Calculus exam, number 10. As an exam question it is only so-so, but it has a lot of potential for having a discussion of relative accuracy of Riemann sums in relation to the definite integral they approximate. The key to doing this is to look at the graph. The question relates the numerical and the graphical aspect of Riemann sums, two parts of the Rule of Four.
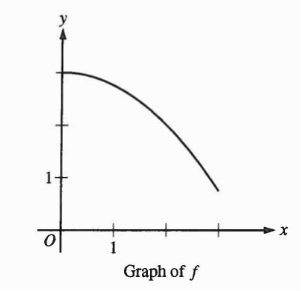
The question presented the graph of a function f, shown below and asked which of five answer choices has the least value. The choices were (which I will call I), the left Riemann sum approximation of the integral, L, the right Riemann sum approximation, R, the Midpoint Riemann sum approximation, M, and a Trapezoidal sum approximation, T. Each of the four approximations were to have 4 subintervals of equal length.
There are important things in the stem – namely that the graph is strictly decreasing and concave downward, and one unimportant thing – the number of subdivisions. As long as the graph is strictly monotonic and does not change concavity the number of subdivisions does not matter; the relative size of the five quantities will be the same. Therefore, to see which is least we can look at one subdivision covering the entire interval. That saves a lot of trouble and is worth discussing with your class. Usually, we let the number of subdivisions go off to infinity; here we go the other way.
Looking at a single interval from 1 to 3, it is easy to see by drawing or picturing the rectangle that the least Riemann sum will be R, the right Riemann sum.
So that answers the question, but there is a lot more you can do with the situation. The first that comes to mind is to have your students to put the five values in order from least to greatest. Stop here and try it for yourself.
R is the smallest and L is the largest. Since the top of a trapezoid between the endpoints of the function on the interval lies below the graph of the function, T is less than I.
So far we have R < T < I < L, but where does the midpoint Riemann sum fit in, and why?
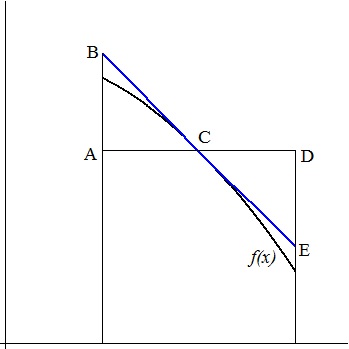
Consider the figure above. C is the midpoint of segment AD.The area of the region between AD and the x-axis is the midpoint approximation. Segment BE is tangent to f(x) at C. Notice that (Why?) and therefore, the area of the region between segment BE and the x-axis is the same as the area between segment AD and the x-axis. The midpoint approximation is the same as the area a trapezoid whose side is tangent to the graph at the midpoint of the interval and extending to the sides of the interval. So the midpoint approximation of the integral is greater than the integral. (The midpoint rectangle as the same area as the “midpoint trapezoid” and distinguishes it from the endpoint trapezoid).
Then R < T < I < M < L.
At least in this case.
In this case, the function was strictly decreasing and concave down. Have your class investigate other combinations of increasing and decreasing functions that are concave up and concave down. Ask your students, individually or in small groups, to investigate these different cases, and discover and justify that:
- There are four cases in all.
- The left sum is greatest, and the right sum is least when the function is strictly decreasing.
- The left sum is least, and the right sum is greatest when the function is strictly increasing.
- When the function is concave down, the endpoint trapezoid lies below the graph of the function and the midpoint trapezoid lies above the graph, therefore T < I < M.
- When the function is concave up, the endpoint trapezoid lies above the graph of the function and the midpoint trapezoid lies below the graph, therefore M < I < T.
- Consider cases where the function is below the x-axis.

I love this question. It’s always funny to me that the kids that spend time worrying about the number of rectangles are usually the ones that get it wrong!
LikeLike