Another way to practice the derivative rules.
The graph below shows two piecewise defined functions, f and g, each consisting of two line segments.
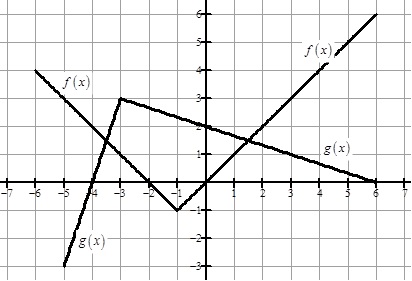
- If
calculate
- If
calculate
- If
calculate
- If
calculate
- Write the equation of the line tangent to the graph of
at the point
.
There are a lot more like these that you can ask from the same graph; or make up your own graph and questions.
Answers: 1. -17/3, 2. 6, 3. 75, 4. -1/3, 5. y = 2 + 6(x + 4) (Corrected 10-3-12 19:10)

Pingback: Seeing the Chain Rule | MATHMANMCQ
Hi Lin,
Thank you for posting this and the derivatives of tabular functions. We used the graphing one today in class and I think there are a couple of typos. I think for number 1 you mean h'(3) and the answer would be -17/3?
LikeLike
Typos. you are correct. Thanks for catching that. I have corrected the post.
LikeLike