Category Archives: Trigonometry

Why Radian Measure?

Posted on by
3

I’m sure you’ve been wondering since you first heard about radian measure before calculus why calculus is always done in radian measure. Once you’ve learned the derivatives of the trigonometric functions, you will appreciate why radians are pretty much the only choice for calculus people.

The idea for this series of posts, The Why Series, a this post I wrote a few years ago called “Why Radians?”  The post gets a lot of ‘hits’ every year. While that post was written for teachers, there is no reason you, a student, shouldn’t read it as well; it’s not a secret. Or maybe it is, but now that you’re initiated into calculus, you may read it.

If you’re still wondering why calculus people use radians, follow this link: Why Radians?

AP Calculus Course and Exam Description Unit 2 Section 7.

A Problem with 4 Solutions and 2 Morals

Posted on by
1

A friend of mine e-mailed me yesterday with a question: Her class was using the Law of Cosines and came up with a solution of \sqrt{8-4\sqrt{3}}, but the “correct” answer was \sqrt{2}\left( \sqrt{3}-1 \right). She wanted to know, having gotten the first answer, how do you get to the second from it. The answers are equivalent: radical I figured it out this way

\sqrt{8-4\sqrt{3}}=\sqrt{6-4\sqrt{3}+2}=\sqrt{{{\left( \sqrt{6}-\sqrt{2} \right)}^{2}}}=\left| \sqrt{6}-\sqrt{2} \right|=\sqrt{2}\left( \sqrt{3}-1 \right)

But in fact, I had worked that from the second back to the first. So I sent the problem to another friend who sent this back: radical 5 This is a more formal way of what I did. (The solution k = 6 gives the same expression.) But the real question is how is a student supposed to know any of this? My friend wrote, “This problem seems really complicated for multiple=choice.  Remember that this is what we had to do AFTER we had done law of cosines to get to that first step.” I agree. Then I asked her for the original problem, which is what I should have done in the first place. The original problem was to find the base of an isosceles triangle with a vertex angle of 30o and congruent sides of 2. 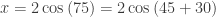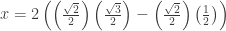Well that’s a whole different story:  radical 3 x=2\cos \left( 75 \right)=2\cos \left( 45+30 \right) x=2\left( \cos (45)\cos (30)-\sin (45)\sin (30) \right) x=2\left( \left( \frac{\sqrt{2}}{2} \right)\left( \frac{\sqrt{3}}{2} \right)-\left( \frac{\sqrt{2}}{2} \right)\left( \frac{1}{2} \right) \right) Base=2x=\sqrt{6}-\sqrt{2} And also x=2\sin \left( 15 \right)=2\sin \left( 45-30 \right) works the same way. 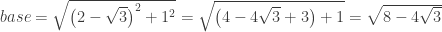But there is yet another way: we could draw a different perpendicular and get a 30-60-90 triangle (not to scale): radical 4b Then using the Pythagorean Theorem on the lower triangle: base=\sqrt{{{\left( 2-\sqrt{3} \right)}^{2}}+{{1}^{2}}}=\sqrt{\left( 4-4\sqrt{3}+3 \right)+1}=\sqrt{8-4\sqrt{3}}

The morals of the story:

  • First as we have all discovered, when a student asks, “What do I do now?” or “How can I get from here to here?” Go back to the original question. Do not jump in the middle and answer the wrong question.
  • Second, while I am definitely not against multiple-choice problems, this is a horrible multiple-choice question. It is horrible because there are so many good ways to do it, but they lead to different looking answers. Students should not be penalized for doing good mathematics. It is fine to require a student to do a problem by a certain method if you are currently teaching that method. But with no method specified, the students should not get a correct answer and then have to really struggle to get your answer. On the other hand, this is a very good questions, precisely because there are so many ways to do it and because the answers look different.