Why Infinity?

Posted on August 25, 2023 by Lin McMullin

First, right from the start: Infinity is NOT a number.

Lots of folks think of infinity as the largest number possible, greater than anything else. That’s understandable because infinity, denoted by the symbol $\displaystyle \infty$ , is often used that way by those unlucky folks who don’t understand mathematics.

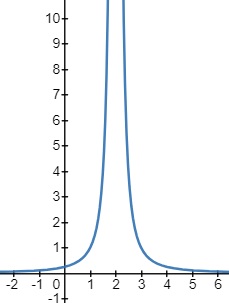
We’ll start with an example: Consider the fraction $\displaystyle \frac{1}{{{{{\left( {x-3} \right)}}^{2}}}}$ . This fraction has no value when x = 3 because there the denominator is zero. And you cannot divide by zero. Nothing personal, no one, no matter how smart, can divide by zero. Ever. Permanently and forever not allowed. Don’t even think about it! (Actually, think about it; just don’t do it.)

What you should say in such cases is that the expression has no value, or is “undefined,” or “the limit does not exist,” abbreviated DNE.

In situations like the example we say, “the limit of the fraction as x approaches 3 equals infinity,” abbreviated $\displaystyle \underset{{x\to 3}}{\mathop{{\lim }}}\,\frac{1}{{{{{\left( {x-3} \right)}}^{2}}}}=\infty$ . This means that the expression gets larger as x gets closer to three. The expression will be greater than any (large) number you want, if you are close enough to three.

You don’t believe me? Okay pick a large number, maybe $\displaystyle {{10}^{8}}$ . I say pick any value for x between 2.9999 and 3.0001 ( $\displaystyle 3-{{10}^{{-4}}}<x<3+{{10}^{4}}$ ) and the expression will be larger than $\displaystyle {{10}^{8}}$ . Try it on your calculator.

How about $\displaystyle {{10}^{{20}}}$ ? Try a number between 2.9999999999 and 3.0000000001. I can play this game all day.

Try graphing the $\displaystyle y=\frac{1}{{{{{\left( {x-3} \right)}}^{2}}}}$ on your calculator. (Hint: Whenever you come across something like this, it is a great idea to graph the expression on your graphing calculator. Graphs can help you see what’s going on. Keep that in mind for the future.)

That’s the way to think about infinity: Infinity is what you say when you’re working with an expression that grows greater than any number you choose.

You may also use infinity to say what happens all the way to the left or right of the graph, its end behavior. The variable, x, may “approach infinity,” that is x moves further to the right (or is greater than any number you choose) the fraction above gets closer to zero: $\displaystyle \underset{{x\to \infty }}{\mathop{{\lim }}}\,\frac{1}{{{{{\left( {x-3} \right)}}^{2}}}}=0$ .

You may not do arithmetic with infinity.

$\displaystyle \infty +\infty \ne 2\infty$

$\displaystyle \infty -\infty \ne 0$

Arithmetic is for numbers.

You will see a number of expressions whose limit is equal to infinity, like $\displaystyle \underset{{x\to 3}}{\mathop{{\lim }}}\,\frac{1}{{{{{\left( {x-3} \right)}}^{2}}}}=\infty$ . Which really means, just what we saw above: that as you (not “you” but x) get closer to 3, the value of the expression will be greater than any number you pick. The $\displaystyle \infty$ symbol is a shorthand way of saying this.

The opposite of infinity, $\displaystyle -\infty$ , sometimes called “negative infinity,” means that the expression gets less than (i.e. more negative), than any negative number you choose.

Even though the expression has no limit, you are allowed to say the limit equals infinity. That’s funny when you think about it. It might be better if everyone said “undefined” or DNE, but they don’t. What can I say?

A word of warning: You may only say “equals infinity” is situations like the example above.

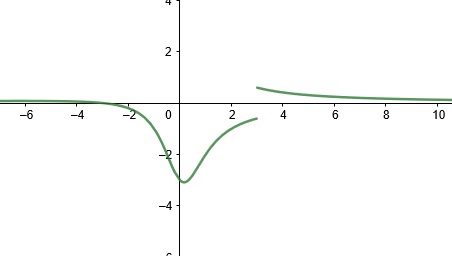
There are other similar expressions that have no limit where it is incorrect to say the limit equals infinity. For example,

$\displaystyle \frac{{\left| x \right|}}{x}$ has no value, is “undefined,” when x = 0, but $\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\left| x \right|}}{x}\ne \infty$ . (Hint: this is where you should look at a graph on your graphing calculator to see why.)
$\displaystyle \underset{{x\to 3}}{\mathop{{\lim }}}\,\frac{1}{{\left( {x-3} \right)}}$ does not exist. This is very similar to the first example but look at the graph and you’ll see a big difference.

So, good luck and enjoy your limitless journey through the infinite reaches of calculus. (Oh, wait! Can I say that?)

Finally,

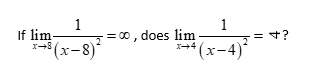
Course and Exam Description Unit 1 topics 1.3, 1.14, 1.5 and others.

Unlimited

Posted on September 7, 2021 by Lin McMullin

Or when is a limit not a limit?

I was discussing the definition of a limit equal to infinity with someone recently. It occurred to me that such functions have no limit! Of course, you say that’s why – sometimes – we say “infinity”. But should we? What does “∞” mean?

The definition we were discussing is this:

$\underset{{x\to a}}{\mathop{{\lim }}}\,f\left( x \right)=\infty \text{ if, and only if, for any }M>0\text{ there is a number }\delta >0\text{ such that}$ $\text{ if }\left| {x-a} \right|<\delta \text{, then }f(x)>M.$

What is being defined here?

What this definition says is that if we can always find numbers close to x = a that make the function’s value larger than any (every, all) positive number we pick, then we say that the limit is (equal to) infinity (∞).

This is how we say mathematically that every (any, all) number in the open interval defined by $\left| {x=a} \right|<\delta$ , also known as $a-\delta <x<a+\delta$ , will generate function values greater than M.

For example, if $\displaystyle f\left( x \right)=\frac{1}{{{{{\left( {x-2} \right)}}^{2}}}}$ , then $\displaystyle \delta =\frac{1}{{\sqrt{M}}}$ will do the trick, since if

$\displaystyle 0<\left| {x-2} \right|<\frac{1}{{\sqrt{M}}}$

$\displaystyle \Rightarrow \sqrt{M}>\left| {\frac{1}{{x-2}}} \right|$

$\displaystyle \Rightarrow M>\frac{1}{{{{{\left( {x-2} \right)}}^{2}}}}$

The function has no value at exactly x = 2. As x get closer to 2, the graph just goes up and up; the values will eventually be greater than any value you choose. The line, x = 2 that the graph never gets to is called an asymptote. An asymptote is the graphical manifestation of a limit of infinity.

But wait a minute: this function has no limit; the values are unlimited. They just get larger and larger. It is correct to say, $\underset{{x\to 2}}{\mathop{{\lim }}}\,\frac{1}{{{{{\left( {x-2} \right)}}^{2}}}}\text{ does not exist}$ . So, which is it “infinity” or does not exist”?

What is this ∞ thing?

An equal sign means that the numbers on both sides are the same. Now the limit part should be a number, but ∞ is not. So how can they be the same?

Is this an abuse of notation?

A definition must be phrased using previously defined terms. Have we defined ∞?

Up to the beginning of the calculus, we probably told students that infinity means something is greater than any value you choose. That’s true, but not much of a definition. (I hope you did not say “a number greater that any number you choose” or “the largest number,” because infinity is not a number.)

How can we tell if something is greater than any value we choose? The answer is that is exactly what the definition quoted above says! It defines what to say about situation where a function’s values get greater and greater, where they are unlimited. In doing so, it defines infinity as much as anything else, and maybe more so.

Disclaimer: There are functions whose limits fail to exist for other reasons and that “infinity” is not an appropriate description in those situations.

For example, $\displaystyle \underset{{x\to 3}}{\mathop{{\lim }}}\,\frac{{{{x}^{2}}-9}}{{\left( {{{x}^{2}}+1} \right)\sqrt{{{{{\left( {x-3} \right)}}^{2}}}}}}$ does not exist and is not ∞ .

$\displaystyle f(x)=\frac{{{{x}^{2}}-9}}{{\left( {{{x}^{2}}+1} \right)\sqrt{{{{{\left( {x-3} \right)}}^{2}}}}}}$ has a finite jump discontinuity at x = 3.

$\displaystyle f(x)=\frac{{{{x}^{2}}-9}}{{\left( {{{x}^{2}}+1} \right)\sqrt{{{{{\left( {x-3} \right)}}^{2}}}}}}$ has a finite jump discontinuity at x = 3.

Infinite Musings

Posted on August 20, 2019 by Lin McMullin

Students get confused about infinity, $\infty$ , because they think of it as a number, because $\infty$ used like a number. Even though they know there is no largest number, they think of infinity as the largest number.

In studying limits, the starting point of calculus, infinite limits come up early on. We tell them $\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{1}{{{{x}^{2}}}}=\infty$ . But what we really mean, and what this symbol means, is that by taking x close enough to 0, $\displaystyle\frac{1}{{{{x}^{2}}}}$ eventually becomes larger that any number they choose, no matter how large.

So, instead why don’t we just say $\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{1}{{{{x}^{2}}}}>M$ where M is any real number? (And as I always suggest when you see the word “any” replace it with “every” and “all.”

- $\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{1}{{{{x}^{2}}}}>M$ where M is any real number

- $\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{1}{{{{x}^{2}}}}>M$ where M represents every real number

- $\displaystyle\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{1}{{{{x}^{2}}}}>M$ where M is all real numbers

Likewise, $\displaystyle \underset{{x\to 2}}{\mathop{{\lim }}}\,\frac{{-1}}{{{{{\left( {x-2} \right)}}^{2}}}}<N$ where N is any number, instead of saying the limit is $-\infty$ .

Infinity, $\infty$ , is really defined by this idea; it’s what “infinity” means.

Consider, $\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{1}{x}$ . Here, you cannot say the expression is larger than any number (because of the negative values approaching zero from the left), so obviously there is no limit, the limit does not exist, DNE, and using $\infty$ is wrong).

To answer my own question, we don’t do this because we’d have to change all the calculus books, and that’s not going to happen. So, don’t do it. Maybe you can start with this and then quickly switch over to the shorthand version $\infty$ .

For more on using $\infty$ and DNE see the post Finding Limits and Good Question 5

Dominance

Posted on August 8, 2012 by Lin McMullin

When considering functions made up of the sums, differences, products or quotients of different sorts of functions (polynomials, exponentials and logarithms), or different powers of the same sort of function we say that one function dominates the other. This means that as x approaches infinity or negative infinity, the graph will eventually look like the dominating function.

Exponentials dominate polynomials,
Polynomials dominate logarithms,
Among exponentials, larger bases dominate smaller,
Among polynomials, higher powers dominate lower,

For example, consider the function $x{{e}^{x}}$ . The exponential function dominates the polynomial. As $x\to \infty$ , the graph looks like an exponential approaching infinity; that is, $\displaystyle \underset{x\to \infty }{\mathop{\lim }}\,x{{e}^{x}}=\infty$ . As $x\to -\infty$ the graph looks like an exponential with very small negative values (i.e. small in absolute value); so, $\displaystyle \underset{x\to -\,\infty }{\mathop{\lim }}\,x{{e}^{x}}=0$ .

Another example, consider a rational function (the quotient of two polynomials). If the numerator is of higher degree than the denominator, as $x\to \pm \infty$ the numerator dominates, and the limit is infinite. If the denominator is of higher degree, the denominator dominates, and the limit is zero. (And if they are of the same degree, then the limit is the ratio of the leading coefficients. Dominance does not apply.)

Dominance works in other ways as well. Consider the graphs of $y=3{{x}^{2}}$ and $y={{2}^{x}}$ . In a standard graphing window, the graphs appear to intersect twice. But on the right side the exponential function is lower than the polynomial. Look farther out and farther up, the exponential dominates and will eventually lie above the polynomial (after x = 7.334).

Here’s an example that pretty much has to be done using the dominance approach.

$\displaystyle \underset{x\to \infty }{\mathop{\lim }}\,\frac{\ln \left( {{x}^{5}} \right)}{{{x}^{0.02}}}=0$

The polynomial function in the denominator, even with the very small exponent, will dominate the logarithm function. The denominator will eventually get larger than the numerator and drive the quotient towards zero. We will return to this function when we know about finding maximums and points of inflection and find where it starts decreasing. For more on this see my post Far Out!

Finding Limits

Posted on August 4, 2012 by Lin McMullin

Ways to find limits (summary):

If the function is continuous at the value x approaches, then substitute that value and the number you get will be the limit.
If the function is not continuous at the value x approaches, then
1. If you get something that is not zero divided by zero, the limit does not exist (DNE) or equals infinity (see below).
2. If you get $\frac{0}{0}$ or $\frac{\infty }{\infty }$ the limit may exist. Simplify by factoring, or using different trig functions. Later in the year a method called L’Hôpital’s Rule can often be used in this situation.
Dominance is a quick way of finding many limits. Exponentials dominate, polynomials, polynomials dominate logarithms, higher powers dominate lower powers. The next post will give some hints about dominance.

Infinity is not a number, but it often is used as if it were. When we say a limit is infinity, what we mean is that the function increases without bound, or there is some x-value that will make the expression larger than any number you choose. Writing things like $\infty -\infty =0,\frac{\infty }{\infty }=1,\infty +\infty =2\infty$ are common mistakes.

DNE or Infinity? $\displaystyle \underset{x\to 3}{\mathop{\lim }}\,\frac{1}{{{\left( x-3 \right)}^{2}}}$ does not exist, and DNE is a correct answer. However, it is a bit better to say the limit is (equals) infinity, indicating that the expression gets larger without bound as x approaches 3. Both answers will get credit on an AP exam. $\displaystyle \underset{x\to 3}{\mathop{\lim }}\,\frac{1}{x-3}$ DNE since the one-sided limits (from the left and from the right) are different. Only DNE gets credit here.

Take a look at this AP question 1998 AB-2: In (a) students found that $\displaystyle \underset{x\to \infty }{\mathop{\lim }}\,2x{{e}^{2x}}=\infty \text{ or }DNE$ , in (b) they found the minimum value of $2x{{e}^{2x}}$ is $-{{e}^{-1}}$ and in (c) they had to state the range of the function is $[-{{e}^{-1}},\infty )\text{ or }x>-{{e}^{-1}}$ . Thus making the students show they knew that this kind of DNE is the kind where the value increases without bound.